在 6 月 22 日的北京智源大会上，美国西北大学教授 Jorge Nocedal 就非线性优化问题进行了十分细致的讲解。
Jorge Nocedal 教授同时还是冯诺伊曼理论奖得主，美国国家工程院院士，以及美国工业和应用数学学会会士，在非线性优化方面曾作出杰出的贡献。他在此次会议上演讲的题目是机器学习中零阶优化方法及其应用（zero-order optimization methods with applications inn machine learning）。
在开始谈论非线性优化问题前，Jorge Nocedal 教授首先介绍了非线性优化问题出现的背景。Jorge Nocedal 教授认为，现今深度神经网络非常成功的背后，实际上包含了很多“运气”成分。
具体来说，深度神经网络主要基于 2 个思想：其一是适合生成表示的预测函数结构，其二是帮助寻找到合适的预测函数的反向传播算法。这里，反向传播算法通常意味着使用梯度下降的方法进行优化。然而，优化过程中使用梯度下降法并不一定保证获得的解能够收敛到我们期望的最小值。
事实上，在不同的搜索空间结构情况下，梯度下降法获得的效果不尽相同，甚至有时弊大于利。但对于“幸运”的深度学习来讲，我们经常遇到的是凸优化问题，因而梯度下降法取得了良好的结果。但对于强化学习，我们则不大可能总是有这么好的运气。
因此，那些“不怎么幸运”的情况下如何进行优化的问题就是此次 Jorge Nocedal 教授演讲的主题。具体来说，假设我们希望最小化一个非线性函数，这个函数需要是光滑的（但并不需要是凸的），我们可以获得函数的估值但不知道它的梯度，同时，函数估值包含了噪声，那么，对一个有着上千个变量的这样的函数来说，是否存在一种算法能够很好的处理这类函数的优化问题？
目前来说，这仍是一个十分前沿的问题，我们还不能获得“最好算法”的确切答案。但 Jorge Nocedal 教授提出了解决这一问题的一种思路。这一思路将尝试计算梯度和噪声的近似值，并通过对噪声的拟牛顿法更新建立二次模型。
假设有一个光滑的函数(x)，但我们无法直接观察(x)而只能观察到包括了(x)和噪声的f(x)，那么我们希望在只观察f(x)的情况下最小化(x)并计算出梯度近似值 g。
图 黑箱的输入和输出及目标函数之间的关系
在进行噪声计算时，我们需要考虑一些不同的场景。其中一个场景是，我们需要自适应的方法或是迭代线性求解，而另一个场景是，我们需要考虑包括舍入误差在内的随机误差。我们希望我们的方法可以适用于这些不同的场景。同时，对深度神经网络的对抗训练，我们可以观察深度神经网络的输入和输出，但不进行反向传播计算，而是对灵敏度进行分析。
这里假设是一个图像分类问题，那么，我们可以通过改变图像的一些部分获得完全不同的分类结果。我们主要对这些变化的部分进行分析，而不需要知道模型的导数，或是神经网络的各种公式。
图 灵敏度分析的一个例子
我们可以只考虑分类不正确的样本。这里会有一些复杂的目标，考虑函数的近似和环境的随机性，这一问题可通过策略梯度方法进行处理。但策略梯度的方法仍然需要涉及到导数。我们这里将通过不涉及导数的方法，即零阶优化方法处理。
零阶优化有很多不同的算法，包括随机搜索或是移至最佳点等。虽然这些方法看起来十分简单粗暴，但许多优化实践就是依赖于这种看起来不怎么好的方法，同时这些方法在困难问题上的复杂度与其他更智能的算法一样高。不过，Moray 和 Wild 曾研究过这些不同的方法，并发现其中最好的方法是根据函数的观察值建立目标函数的二次模型。
我们需要一个完整的 Hessian 矩阵以创建这样的二次模型，不过，我们可以在二次模型中插值，这就可以减少我们需要的信息量，然后将模型最小化至置信域。
图 目标函数二次模型的建立
这一方法并不怎么需要计算出比较好的梯度估计，而更多强调的是二次模型整体的质量。同时，这一方法也有它的不足之处：这一方法依赖于对置信域的估计，置信域过大或过小都会对结果产生影响；且这一方法不能并行化，也就是说一次只能计算一个函数值。对于这些问题，我们认为应该有更好的解决方法，因此我们提出了以下策略。
我们认为，应当要更多的对梯度进行估值，并使用拟牛顿法构建二次模型。其中，BFGS 算法已经被相当广泛地使用在包括机器学习在内的很多领域，有着很好的性能。
这里，我们需要考虑对带有噪声的函数的梯度进行估值。首先，我们可以对一个很近的区间范围内求平均，即从带有噪声的函数获得一个光滑的函数，然后求这个光滑函数的梯度。这个计算方法看起来像是有限差分，通过移动一段距离，用有限差分近似值乘以移动的方向，然后根据计算结果更新下一次计算，最后获得函数梯度的估值。
图 对带有噪声的函数进行光滑
因此，我们需要估计函数的噪声水平，这就涉及到如何选取有限差分区间。如果我们选择了过小的有限差分区间，这个函数与真实函数的斜率将不匹配，如下图所示。但如果我们选择了 0.28 作为有限差分区间，我们将获得一个很合理的近似函数。所以这部分需要我们不断努力，选择一个随机方向，获得函数在沿着这个方向上的等距点上的估值。
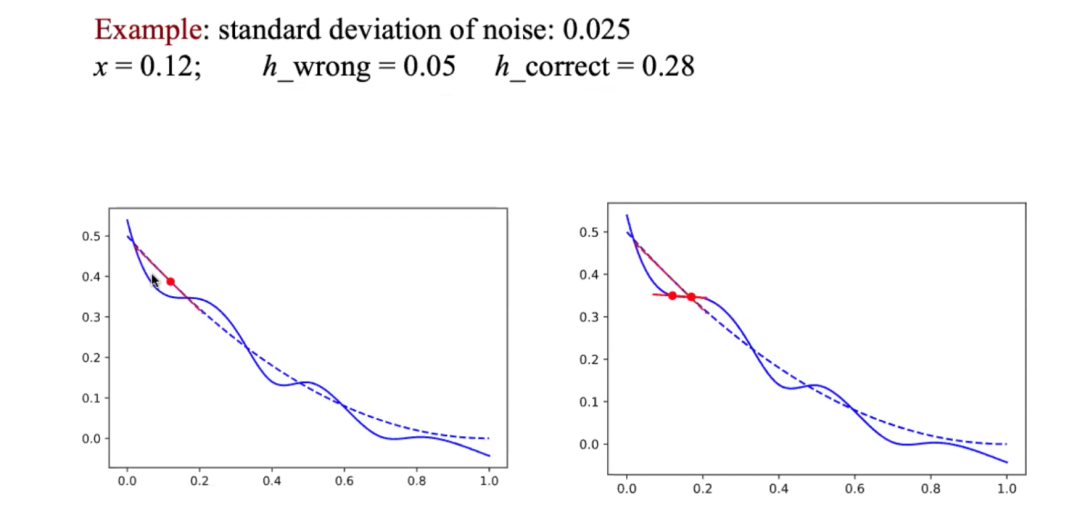图 不同的有限差分区间可能导致对函数不同的光滑效果
现在，我们获得了沿着这条线上几个点的函数估值，假设这里的我们计算了 7 个点，然后计算函数在这几个点之间的差，这会获得 6 个数值，我们继续重复这样的计算，并获得了如下图这样的表。对于光滑的函数来说，更高阶的差分会逐渐趋向于 0，而有噪声的函数则会一直停留在某个值附近。我们可以据此来估计函数的噪声水平。
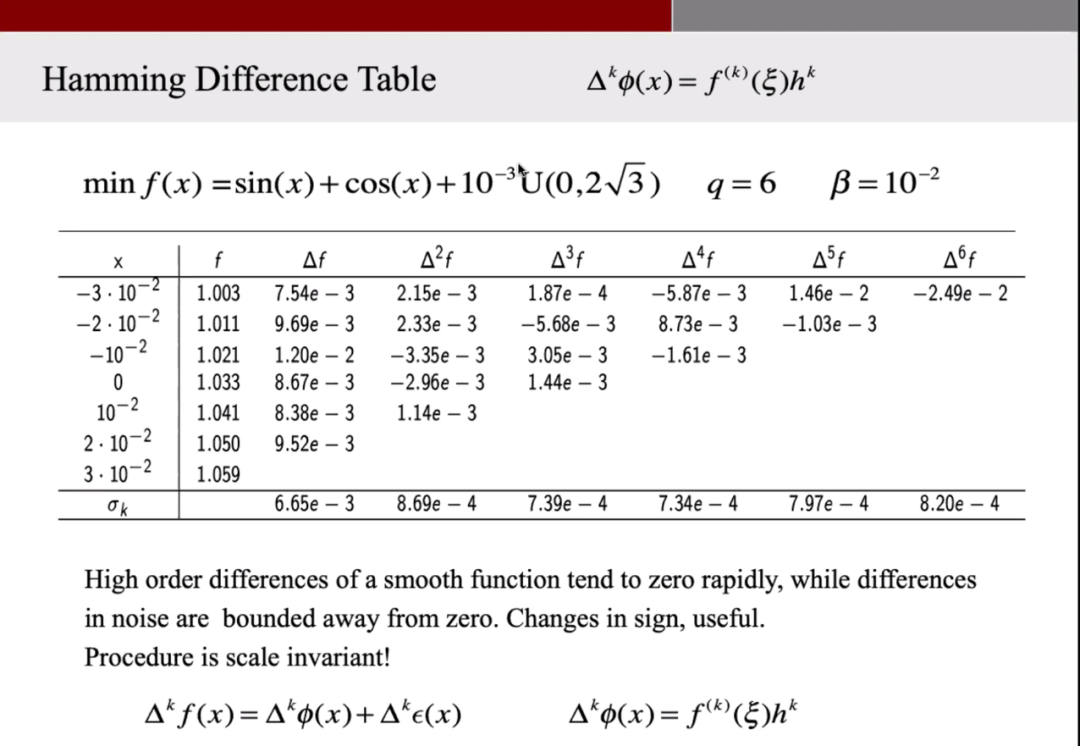图 通过差分获得函数噪声水平
一旦我们获得了函数噪声的水平，我们就可以对有限差分区间进行估计，进而实现上述的对函数梯度的估算。既然我们有了函数梯度的估计值，为什么我们不直接建立拟牛顿模型，如噪声有限差分 BFGS 模型？实际上目前还没有人这么做。主要原因是对噪声函数的差分是十分危险的，不好的迭代可以造成灾难性后果。
因此，在我们的算法中，我们将在每次计算中都对噪声进行估计，并据此估计有限差分区间。然后计算拟牛顿法的搜索方向并进行线搜索。当线搜索失败时，通过调整线搜索或是重新估计噪声水平进行更正。这里线搜索起到了 2 个作用：其一是在有限差分区间合适的情况下帮助决定步长，其二是帮助决定是否需要重新估计噪声水平。
图 Jorge Nocedal教授提出的算法
以上就是 Nocedal 教授演讲的主要内容。虽然 Nocedal 教授今年已是 72 岁高龄并光环缠身，但仍然十分谦虚。他在开篇就提到，自己的成果离不开合作者。同时，Nocedal 教授在学术领域也正在持续创造辉煌，可以说是老当益壮。据 google scholar 统计，Nocedal 教授近年来论文引用情况保持持续走高趋势。
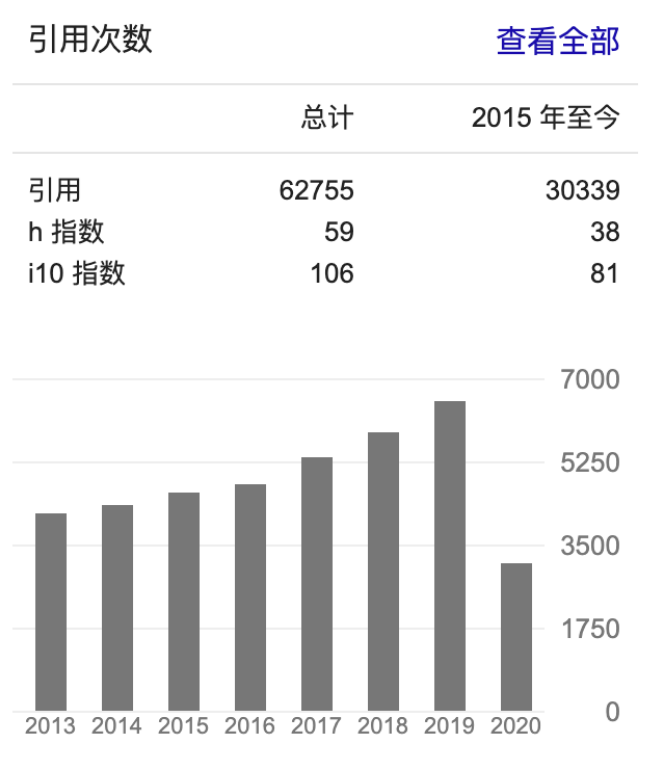图 Nocedal 教授近年发表论文的饮用情况统计（数据来源：Google scholar）
想要机器学习更好地在不同领域应用，除了需要将实际问题转化成数学优化问题，还要有更核心的优化方法以获得更好的学习效果。但寻找到“最好”的优化方法仍然任重而道远。在此次会议上 Nocedal 教授分享了他近年来在该领域的一些进展，希望能够启发更多该领域的学者。
喜欢本篇内容，请点在看
