机器学习 - 训练集、验证集、测试集

随机森林与其他机器学习方法不同的是存在OOB，相当于自带多套训练集和测试集，自己内部就可以通过OOB值作为评估模型准确度的一个方式。其他多数机器学习方法都没有这一优势。

通常在有了一套数据时，需要拆分为训练集、测试集。数据集一般按比例8:2,7:3，6:4等分为训练集和测试集。如果数据集很大，测试集不需要完全按比例分配，够用就好。

测试集完全不用于训练模型。训练集在训练模型时可能会出现过拟合问题（过拟合指模型可以很好的匹配训练数据但预测其它数据时效果不好），所以一般需要在训练集中再分出一部分作为验证集，用于评估模型的训练效果和调整模型的超参数 (hyperparameter)。

如下图，展示了一套数据集的一般分配方式：

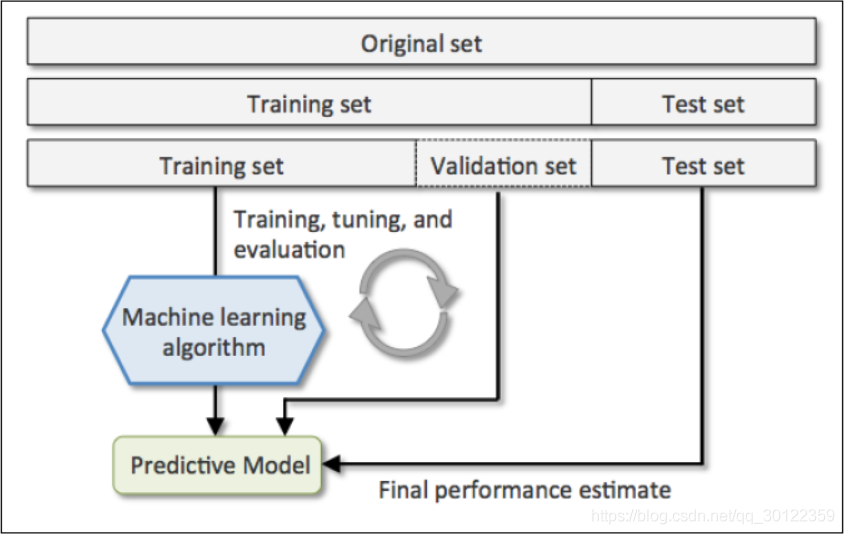
训练集用于构建模型。
验证集用于评估模型的一般错误率，并且基于此调整超参数（hyperparameter，如随机森林中的mtry），获得当前最优模型。
验证集不是必须的。
如果不需要调整超参数，则可以不用验证集。
验证集获得的评估结果不是模型的最终效果，而是基于当前数据的调优结果。
使用所有训练集（含从中分出的验证集）数据和选择的最优超参数完成最终模型构建。
测试集测试评估最终模型指标，如准确率、敏感性等。

通俗地讲，训练集等同于学习知识，验证集等同于课后测验检测学习效果并且查漏补缺。测试集是期末考试评估这个模型到底怎样。

可参考的分配规则：

对于小规模样本集（几万量级），常用的分配比例是 60% 训练集、20%验证集、20% 测试集。
对于大规模样本集（百万级以上），只要验证集和测试集的数量足够即可，例如有 100 w 条数据，那么留 1 w 验证集，1 w 测试集即可。
1000 w 的数据，同样留 1 w 验证集和 1 w 测试集。
超参数越少，或者超参数很容易调整，那么可以减少验证集的比例，更多的分配给训练集。

训练集中的数据我们希望能更多地应用于训练，但也需要验证集初步评估模型和校正模型。

简单交叉验证

简单交叉验证是从训练集中选择一部分（如70%）作为新训练集，剩余一部分（如30%）作为验证集。基于此选出最合适模型或最优模型参数。然后再用全部的训练集训练该选择的模型。其在一定程度上可以避免过拟合事件的发生。但基于70%训练集评估的最优模型是否等同于基于所有训练集的最优模型存疑。不同大小的验证集获得的评估结果差异较大，单纯按比例划分会导致无法选到最好的模型。另外如果训练集较小再如此分割后，训练集数目就更少了，不利于获得较好的训练模型。

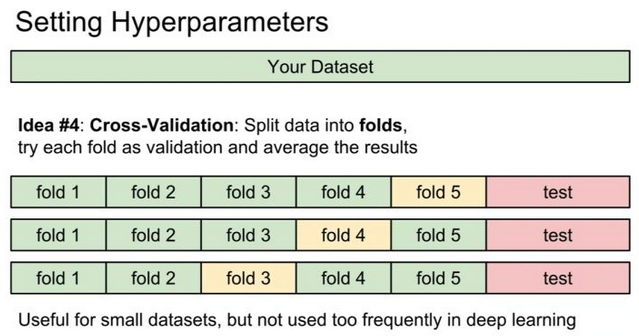
K-fold交叉验证

所以就提出了交叉验证的操作，最常用的是K-fold交叉验证 (k-fold cross validation) 。

其目的是重复使用原始训练集中的数据，每一个样品都会被作为训练集参与训练模型，也会作为测试集参与评估模型。最大程度地利用了全部数据，当然也消耗了更多计算时间。

其操作过程如下：

将训练集分成K份（如果训练集有m个样本，则每一份子集有m/K的样本；
若不能整除其中一个集合会样本较少。
）
对于每一个模型（如随机森林中不同的mtry值，mtry=2,mtry=10时分别会构建出不同的模型；
或不同的算法如随机森林、支持向量机、logistic 回归等） for j in 1, 2, 3, … K: 将训练集中除去第j份数据作为新训练集，用于训练模型用第j份数据测试模型，获得该模型错误率
经过第2步就得到了1个模型和K个错误率，这K个错误率的均值和方差就是该模型的一般错误率。
对每个模型重复2和3步骤，选择一般错误率最小的模型为当前最优模型。
用所有的数据训练当前的最优模型，获得最终训练结果。
用独立的测试集测试模型错误率。

这一操作的优点是：

所有训练集的样品都参与了每个模型的训练，最大程度利用了数据。
多个验证集多次评估，能更好的反应模型的预测性能。

下一步的关键就是如何选取K，通常为5或10（10是最常用的经验值，但根据自己的数据集5，20也都可能获得比较好的结果）。

K越大，新训练集与总训练集大小差别越小，评估偏差也最小。

极端情况下K=m ，每个子数据集都只有 1个样品，这也被称为LOOCV - leave one out-cross validation。

举个例子 - 2折交叉验证

假设有一个数据集，包含6个样品。

# 假设有一个数据集，包含 6 个样品
m = 6
train_set train_set

## [1] "a1" "a2" "a3" "a4" "a5" "a6"

利用其构建2-折交叉验证数据集。

K = 2
set.seed(1)
# 下面这行代码随机从1:K 中有放回的选取与样品数目一致的索引值
# 从属于相同索引值的样本同属于一个fold
kfold kfold

## [1] 1 2 1 1 2 1

从下面数据可以看出，每个子集的大小不同。这通常不是我们期望的结果。

table(kfold)

## kfold
## 1 2 
## 4 2

修改如下，再次获取kfold:

kfold kfold

## [1] 1 2 2 2 1 1

这次每个fold的样品数目一致了。

# 如果 m/K 不能整除时，最后一个 fold 样本数目会少
table(kfold)

## kfold
## 1 2 
## 3 3

然后构建每个fold的训练集和测试集

current_fold = 1
train_current_fold = train_set[kfold!=current_fold]
validate_current_fold = train_set[kfold==current_fold]

print(paste("Current sub train set:", paste(train_current_fold, collapse=",")))

## [1] "Current sub train set: a2,a3,a4"

print(paste("Current sub validate set:", paste(validate_current_fold, collapse=",")))

## [1] "Current sub validate set: a1,a5,a6"

写个函数循环构建。通过输出，体会下训练集和测试集的样品选择方式。

K_fold_dataset   train_current_fold = train_set[kfold!=current_fold]
  validate_current_fold = train_set[kfold==current_fold]
  c(fold=current_fold, sub_train_set=paste(train_current_fold, collapse=","), sub_validate_set=paste(validate_current_fold, collapse=","))
}

do.call(rbind, lapply(1:K, K_fold_dataset, train_set=train_set, kfold=kfold))

##      fold sub_train_set sub_validate_set
## [1,] "1"  "a2,a3,a4"    "a1,a5,a6"      
## [2,] "2"  "a1,a5,a6"    "a2,a3,a4"

往期精品(点击图片直达文字对应教程)

后台回复“生信宝典福利第一波”或点击阅读原文获取教程合集