大数据文摘授权转载自数据派THU
作者: Samuele Mazzanti
翻译:欧阳锦
校对:王可汗
数据科学家通常根据准确性或准确性来评估其预测模型,但几乎不会问自己:
“我的模型能够预测实际概率吗?”
但是,从商业的角度来看,准确的概率估计是非常有价值的(准确的概率估计有时甚至比好的精度更有价值)。来看一个例子。
想象一下,你的公司正在出售2个杯子,一个是普通的白色杯子,而另一个则上面印有小猫的照片。你必须决定向这位给定的客户展示哪个杯子。为此,你需要预测给定的用户购买每个杯子的可能性。因此,你训练了几个不同的模型,你会得到以下结果:
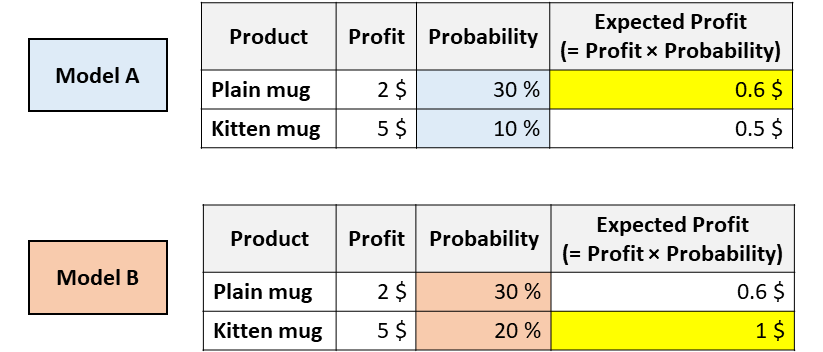
具有相同ROC(receiver operating characteristic)但校准不同的模型。[图源自作者]
现在,你会向该用户推荐哪个杯子?
以上两种模型都认为用户更有可能购买普通马克杯(因此,模型A和模型B在ROC曲线下具有相同的面积,因为这个指标仅仅对分类进行评估)。
但是,根据模型A,你可以通过推荐普通马克杯来最大化预期的利润,然而根据模型B,小猫马克杯可以最大化预期的利润。
在像这样的现实应用中,搞清楚哪种模型能够估算出更好的概率是至关重要的事情。
在本文中,我们将了解如何度量概率的校准(包括视觉和数字),以及如何“纠正”现有模型以获得更好的概率。
Python中所有最流行的机器学习库都有一种称为“ predict_proba”的方法:Scikit-learn(例如LogisticRegression,SVC,RandomForest等),XGBoost,LightGBM,CatBoost,Keras…
但是,尽管它的名字是预测概率,“predict_proba”并不能完全预测概率。实际上,不同的研究(尤其是这个研究和这个研究)表明,最为常见的预测模型并没有进行校准。
数值在0与1之间不代表它就是概率!
但是,什么时候可以说一个数值实际上代表概率呢?
想象一下,你已经训练了一种预测模型来预测患者是否会患上癌症。如果对于给定的患者,模型预测的概率为5%。原则上,我们应该在多个平行宇宙中观察同一位患者,并查看其实际上患上癌症的频率是否为5%。
但是这种观察条件这是不可能发生的事,所以最好的替代方法是将所有概率在5%附近的患者都接受治疗,并计算其中有多少人真的患了癌症。如果观察到的患癌百分比实际上接近5%,则可以说该模型提供的概率是“已校准”的。
当预测的概率反映了真实情况的潜在概率时,这些预测概率被称为“已校准”。
那么,如何检查一个模型是否已校准?
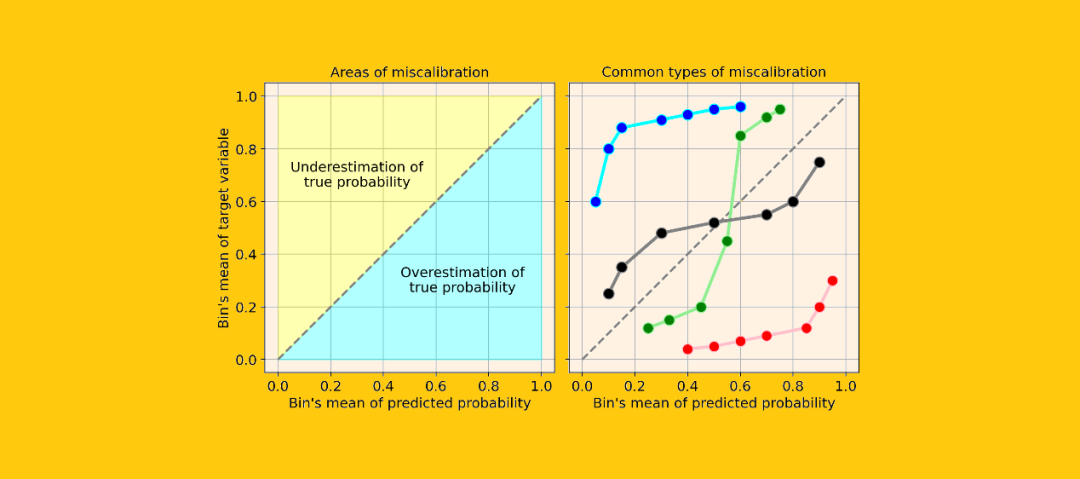
评估一个模型校准的最简单的方法是通过一个称为“校准曲线”的图(也称为“可靠性图”,reliability diagram)。
这个方法主要是将观察到的结果通过概率划分为几类(bin)。因此,属于同一类的观测值具有相近的概率。在这一点上,对于每个类,校准曲线将预测这个类的平均值(即预测概率的平均值),然后将预测概率的平均值与理论平均值(即观察到的目标变量的平均值)进行比较。
Scikit-learn通过“ calibration_curve”函数可以完成所有这些工作:

你只需要确定类的数量和以下两者之间的分类策略(可选)即可:
- “uniform”,一个0-1的间隔被分为n_bins个类,它们都具有相同的宽度;
- “quantile”,类的边缘被定义,从而使得每个类都具有相同数量的观测值。
出于绘图目的,本人更喜欢“quantile”的分类策略。实际上,“uniform”分类可能会引起误导,因为有些类中可能只包含很少的观察结果。Numpy函数给每个分类返回两个数组,每个数组包含平均概率和目标变量的平均值。因此,接下来要做的就是绘制它们:假设你的模型具有良好的精度,则校准曲线将单调增加。但这并不意味着模型已被正确校准。实际上,只有在校准曲线非常接近等分线时(即下图中的灰色虚线),您的模型才能得到很好的校准,因为这将意味着预测概率基本上接近理论概率。让我们看一些校准曲线的常见类型的例子,它们表明了模型的校准错误:- 系统高估。与真实分布相比,预测概率的分布整体偏右。当您在正数极少的不平衡数据集上训练模型时,这种错误校准很常见。(如红线)
- 系统低估。与真实分布相比,预测概率的分布整体偏左。(如蓝线)
- 分布中心太重。当“支持向量机和提升树之类的算法趋向于将预测概率推离0和1”(引自《Predicting good probabilities with supervised learning》)时,就会发生这类错误校准。(如绿线)
- 分布的尾巴太重。例如,“其他方法(如朴素贝叶斯)具有相反的偏差(bias),并且倾向于将预测概率趋近于0和1”(引自《Predicting good probabilities with supervised learning》)。(如黑线)
假设你已经训练了一个分类器,该分类器会产生准确但未经校准的概率。概率校准的思想是建立第二个模型(称为校准器),校准器模型能够将你训练的分类器“校准”为实际概率。
请注意,用于训练的第一个分类器的数据不能被用于校准。因此,校准包括了将一个一维矢量(未校准概率)转换为另一个一维矢量(已校准概率)的功能。- 保序回归。一种非参数算法,这种非参数算法将非递减的自由格式行拟合到数据中。行不会减少这一事实是很重要的,因为它遵从原始排序。
看看使用Python如何在玩具数据集中实际应用校准器:
首先,需要拟合一个分类器。这里使用随机森林(或者任何具有“predict_proba”方法的模型都可以)。然后,使用分类器的输出(在验证数据集上)来拟合校准器,并最终预测测试数据集的概率。
每个人都喜欢图片展示的量化效果。但是除了校准图外,我们还需要一种定量的方法来测量校准。最常用的方法称为“预期校准误差(Expected Calibration Error)”,这个方法回答了下面的问题:
定义单个类别(bin)的校准误差很容易:即为预测概率的平均值与同一类别(bin)内的正数所占百分比的绝对差值。如果考虑一下这个定义,它非常直观且符合逻辑。取一个类别(bin),并假设其预测概率的平均值为25%。因此,我们预计该类别中的正数所占百分比大约等于25%。如果这个百分比离25%越远,意味着这个类别(bin)的校准就越差。因此,预期校准误差(Expected Calibration Error, ECE)是单个类别的校准误差的加权平均值,其中每个类别的权重与它包含的观测值的数量成正比:其中b标识一个类别(bin),B是类别(bin)的数量。注意,分母只是样本总数。但是这个公式给我们留下了定义B值(即,类别数量)的问题。为了找到尽可能中性的指标,我建议根据Freedman-Diaconis rule(这是一个统计规则,旨在找到使直方图尽可能接近理论概率分布的B值。)在Python中使用Freedman-Diaconis rule非常简单,因为它已经在numpy的直方图函数中被实现(足以将字符串“ fd”传递给参数“ bins”)。以下是预期校准错误(ECE)的Python实现,默认情况下采用Freedman-Diaconis rule:现在,我们有了一个校准方法,让我们比较上面获得的三个预测概率的模型(在测试集上)的校准情况:正如上图所示,如果你认为普通随机森林的ECE为7%,那么保序回归在校准方面则提供了最好的结果,这可以看作是一个巨大的进步,因为平均来看,使用保序回归的模型,其预测概率距离真实概率只有1.2%。如果你想了解更多概率校准的主题,以下是一些有趣的文章(本文的基石):- «Predicting good probabilities with supervised learning» (2005) by Caruana and Niculescu-Mizil.
- «On Calibration of Modern Neural Networks» (2017) by Guo et al.
- «Obtaining Well Calibrated Probabilities Using Bayesian Binning» (2015) by Naeini et al.
Python’s «predict_proba» Doesn’t Actually Predict Probabilities (and How to Fix It)https://towardsdatascience.com/pythons-predict-proba-doesn-t-actually-predict-probabilities-and-how-to-fix-it-f582c21d63fc