
笔者之前写过一篇名为《用PCA方法进行数据降维》的文章,文章中主要讲述了如何用PCA(主成分分析)来对数据进行降维的方法。而今天笔者将介绍另一种常用的数据降维方法——LDA。
LDA的全称是linear discriminant analysis,即线性判别分析,LDA与PCA一样,都可用于数据降维,但二者既有相似也有区别,PCA主要是从特征/维度的协方差角度,去找到比较好的投影方式,即选择样本点投影具有最大方差的方向,而LDA则是寻找一个投影方向,让原先的数据在这个方向上投影后,不同类别之间数据点距离尽可能大,而同类别数据点距离尽可能小。此外PCA属于无监督式学习,很多情况下需要配合其他算法使用,而LDA属于监督式学习,本身除了可以用于降维外,还可以进行预测分析,说白了就是既可以“团战”,也可以单独打怪。而本文就主要讲述如何用LDA来进行数据分类,当然这里面肯定也会用到降维的原理。
LDA的大致原理如图1所示。图1中左图是按照常规坐标系来分析,这时可以看到数据有部分重叠,在分类时可能会有干扰,这时我们就要找到一个投影方向,让这些数据在这个方向上的投影,做到类之间距离尽可能大,类内数据尽可能聚集,如右图所示。
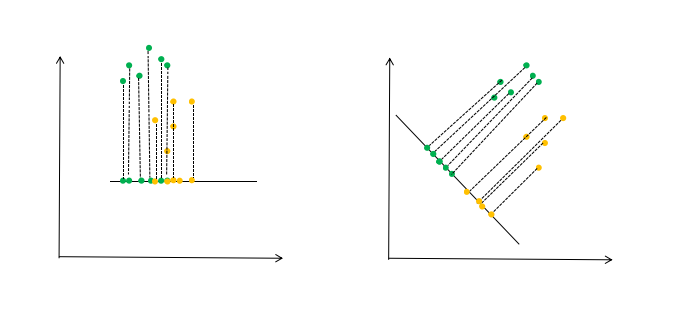
图1. LDA原理图
下面再简单介绍一下LDA的数学原理。
以最简单的两个类别为例,假设Xi、ui、Σi分别表示第i类样本点的集合、均值向量、协方差矩阵,若将数据投影到直线w上,则两类样本的中心在直线上的投影分别是w^Tu1和w^Tu2,在所有样本点都投影到直线上后,两类样本的协方差分别是w^TΣ1w和w^TΣ2w。我们要想让类别之间距离更大、类内距离更小,也就是要使图2中的(1)式最大。在这里我们再定义两个概念,一个是类内散度阵(within-class scatter matrix),即图2中(2)式,一个是类间散度阵(between-class scatter matrix),即图2中(3)式。那么这个让(1)式最大的问题就转化为最大化一个瑞利熵,即最大化(4)式。
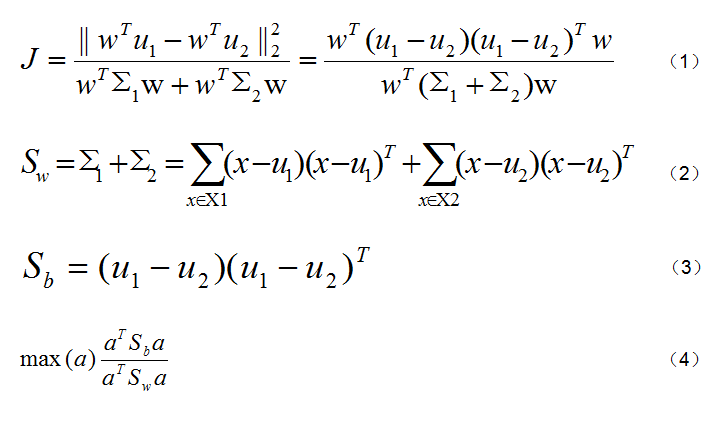
图2. LDA部分推导公式
而求解(4)式也就是相当于求解图3中(5)式,用拉格朗日乘法求解,得到图3中(6)式,这就转化成了一个求特征方程的问题了,也就是求n-1个最大特征值所对应的特征向量(n是维度)。这个按照我们正常求解特征方程就可以了。
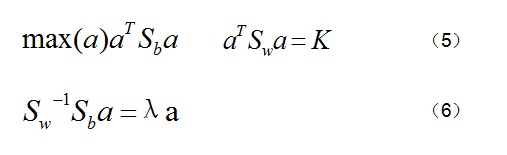
图3. LDA部分推导公式
在实际使用中,如果按照上述原理推导会非常麻烦,但是scikit-learn中已经为我们提供了现成的LDA方法,我们只要直接调用即可,下面就以scikit-learn为例,来看一下LDA在实际使用中的效果。
这次选用的数据集是鸢尾花数据集,来自seaborn库,大小为150行、5列,数据集样例如图4所示。
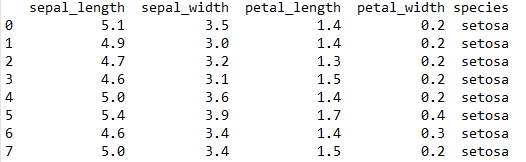
图4. 鸢尾花数据集样例
首先还是导入各种库。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
然后是设置训练数据集和测试数据集。熟悉鸢尾花数据集的人都知道,这个数据集中150个样本点可以分为3个类别,每个类别各有50个样本点,这三个类别是'setosa'、'versicolor'和'virginica',可以用代码set(data['species'].values)来查看这三个值。我们在这里要设置训练集和测试集,就要在每个类别中都取得一定量的数据,笔者的方法是选取总数据集中60%的数据为训练集,即训练集一共是90个样本点,其中每个类别取前30个样本点,而测试集就是剩下的60个样本点,每个类别就是20个,代码如下。
data = sns.load_dataset('iris') #总数据集
data_train = data.iloc[np.r_[0:30, 50:80, 100:130]] #训练集
data_test = data.iloc[np.r_[30:50, 80:100, 130:150]] #测试集
train_x = data_train.iloc[:,:4] #训练集数据
train_y = data_train.iloc[:,4] #训练集分类
test_x = data_test.iloc[:,:4] #测试集数据
test_y = data_test.iloc[:,4] #测试集分类
接下来就是设置分类器,并用分类器进行训练和预测,代码如下。
clf = LDA(n_components=2) #分类器
clf.fit(train_x, train_y) #用数据进行训练
pre_y = clf.predict(test_x) #对测试数据进行预测
这里clf = LDA(n_components=2)中,n_components=2就是我们最终要得到的数据维度数,原数据是4个维度,而这里我们要把它降维到2维,实际上这里我们只能选择2维和1维,因为n_components的默认值是数据集维度数和数据集分类数-1这两个中较小者,本例中维度数是4,数据集分类数-1是2(分类数是3),而这里n_components的值只能小于或等于2,所以我们选2。然后我们输出预测结果,结果如图5所示。
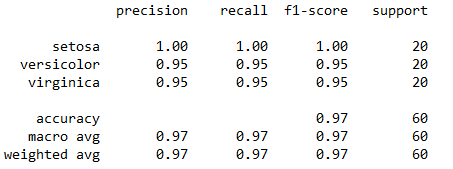
图5. 60%情况下预测结果
从图中可以看到预测效果还是很好的,准确率在95%以上,为了更好地了解LDA的效果,笔者又分别作了两次测试,即分别取总数据集40%和80%的数据为训练集,这里40%的数据量就是60个样本点,每个类别取前20个样品,剩下的60%(也就是90个样本点)为测试集,而80%的情况也同理。这里笔者不再粘贴代码,代码只需对前面代码进行小的修改即可,只附上最终结果,预测的结果如图6和图7所示。
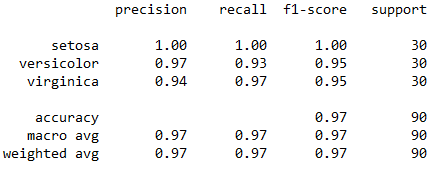
图6. 40%情况下预测结果
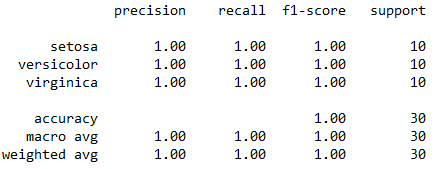
图7. 80%情况下预测结果
从图中我们可以看到,在40%和80%训练量这两种情况下,最终预测的准确率都非常高,40%的条件下和60%的结果几乎一样,而80%的情况下三个类别的预测准确率竟然高达100%。这里笔者推测,准确率如此之高的原因,除了LDA方法的优势之外,可能和我们选用的鸢尾花数据集有关,这个数据集比较简单,其类别比较容易区分,即便选择其他的分类方法,也同样能取得好的效果。而这里还有一个小插曲,LDA方法的提出者Ronald Fisher,同时也是鸢尾花数据集的提出者,用他自己的方法来分析自己的数据集,结果肯定不会差。
本文用scikit-learn来对LDA方法进行了一个说明,并且在案例中也取得了不错的效果,但希望用户不要对LDA的使用过于盲目,其自身依然存在一些不足,比如当样本量远小于样本的特征数时,分类效果会很差,同时LDA不适合对非高斯分布的样本进行降维,LDA还可能过度拟合数据等等。本文源码下载方式请见文末,讨论本文内容可以添加文末“Python小助手”进入微信群交流!
作者简介:Mort,数据分析爱好者,擅长数据可视化,比较关注机器学习领域,希望能和业内朋友多学习交流。
赞 赏 作 者

Python中文社区作为一个去中心化的全球技术社区,以成为全球20万Python中文开发者的精神部落为愿景,目前覆盖各大主流媒体和协作平台,与阿里、腾讯、百度、微软、亚马逊、开源中国、CSDN等业界知名公司和技术社区建立了广泛的联系,拥有来自十多个国家和地区数万名登记会员,会员来自以工信部、清华大学、北京大学、北京邮电大学、中国人民银行、中科院、中金、华为、BAT、谷歌、微软等为代表的政府机关、科研单位、金融机构以及海内外知名公司,全平台近20万开发者关注。
长按扫码添加“Python小助手”
后回复“LDA”获取本文源码

▼点击成为社区会员 喜欢就点个在看吧