电池技术的迅速发展使世界进入了电动汽车EV的新时代。电动汽车发生事故时，其电池组可能会出现灾难性损坏，导致短路，热失控甚至火灾和爆炸。因此，研究每个电池安全运行的条件范围（即“安全范围”）十分重要。研究开发这种安全范围的最大挑战在于需要大量电池故障测试的数据库。麻省理工大学的Juner Zhu和清华大学夏勇教授课题组合作研究，通过建立锂离子电池单元的高精度计算模型来克服挑战，其中所有组件材料都通过精确计算的本构模型进行表征。模拟了极大机械负载条件的大矩阵，并使用机器学习算法获得安全范围。该工作展示了将数值数据生成与数据驱动建模相结合，预测储能系统的安全性的方法，为电动汽车电池的设计和安全范围提供了重要的技术指导。现有的安全性研究主要集中在电池和模块的发热以及更安全的能源材料的创新这些方面，对于引发热失控的机械故障的理解认识一直是电动汽车和电池的盲区。同时，目前仍然没有全球认可的电池安全测试标准或规定，而插电式电动车中大约一半的火灾事故被确认是由机械负载引起的，这可能是车辆或者高速公路物体的碰撞（称为“地面撞击“，如图1A）。在实际的事故中，电池单元可能经历各种机械负载条件（压头的几何形状和质量，加载速度，加载方向等），因此，了解确保电池单元安全运行的条件范围非常重要。创建涵盖所有上述类型的加载和边界条件的测试矩阵是一项艰巨的任务。即使通过学术界和工业界的共同努力，也不可能进行数百或数千次实验。另外，随着新一代电池进入市场，快速变化的电池技术可能使旧的测试过时。最近开发的详细的电池计算模型提供了通过数值模拟取代物理测试的可能。这种模型可以很好地预测实际观察到的变形和破坏模式，包括压实，剪切带定位，屈曲，分层，渐进式断裂和厚度裂纹形成，都会引发电池短路。运行详细的有限元模型的唯一限制是使用成本。这不仅来自提交，运行和后处理计算机模拟的运行时间，而且还来自给新用户培训。而通过创建一个高阶表去开发数据驱动的“安全范围“，人们可以在给定加载情况和边界条件下对电池状态进行快速查找预测。如何从巨大的数据库中提取导致电池故障和电气短路的趋势和参数的关键条件是一个问题。机器学习（ML）技术的最新发展提供了分析大数据的有效工具。在能源领域，它已被用于寻找能源材料的合理设计并了解热力学和电化学过程的机理。该研究中使用了这个强大的工具来开发锂离子软包电池单元的安全范围，并展示了其在电动汽车和电池行业可能的应用。锂离子电池的机械安全性研究涉及多个尺度。图1显示了多尺度建模程序，涵盖三个级别- 电动汽车EV（电池组和模块）级，电池单元级和组件材料级。对EV安全问题的理解遵循从宏观尺度到微尺度的“自上而下”过程。具体来说，意外情况发生在EV水平，但机械变形通常定位在一个单独的电池上，并且机械故障和电短路通常从材料级别中的几层电极开始。相比之下，模型程序是一种“自下而上”的程序。测试和模拟构成材料的机械性能被作为整个电池单元成功的有限元模型的基础。随后，可以将单元级模型应用于各种负载条件的模拟，生成用于电池单元的“安全范围“的数据。其可以用于实际电动汽车EV事故分析。本文建模程序的描述即采用这种自下而上的顺序。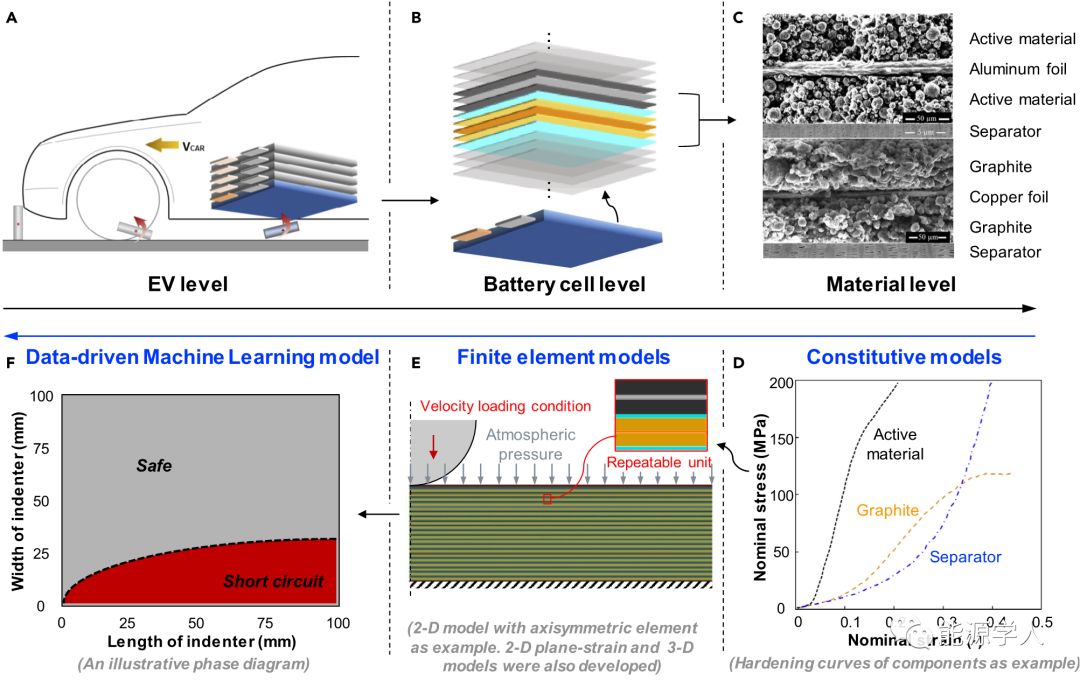
图1. 机械安全性研究的多个尺度和每个尺度的模型。（A-C） 常规“自上而下”的过程：（A）EV级（B）电池级 （C）组件和材料级。比例尺：隔膜为5μm，涂层为50μm。（D-F）建模采用“自下而上”法：（D）材料层面开发；（E）有限元模型的输入；（F）有限元模型为数据开发生成大数据驱动ML模型。本文制定并校准了软包电池的详细计算模型，用于生成输出结果的大数据库。在干燥条件下对电池的构成材料进行了机械试验，包括阳极的石墨涂层，阴极的NMC涂层，集流体，隔膜和铝塑封袋。涂层是典型的粒状材料，其机械性能取决于静水压力并且表现出经受压缩的固结过程（图1D），因此，使用Drucker-Prager/Cap塑性模型（图S1-S4）。集流体和塑封袋是薄金属箔，因此采用具有Johnson-Cook韧性断裂标准的J2塑性模型（图S5）。隔膜是高度多孔的聚合物膜，并且使用可压碎的泡沫塑性模型。通过在不同加载速度下的试验和使用Johnson-Cook型函数模拟硬化曲线的比例来研究组分材料的机械性能的应变率依赖性。电解质不是直接为真实实体建模，而是通过表征速率依赖性来考虑其影响。在电池单元层面，由于颗粒-金属多层结构的复杂性，均匀化，其中所有组分的性质被涂抹成连续模型，文献中存在大量有限元（FE）模型。然而，为了检测定位机械故障和短路，需要一个表征所有电池组件（电极，集流体，隔膜和塑封袋）的详细模型。在材料级别上执行测试和建模程序可以在Abaqus/explicit中开发这样详细的模型（图1E）。2D轴对称，2D平面应变和3D完整模型三种建模策略的前两者对装载条件有严格的要求。当压头是一个小的旋转物体并且加载方向垂直于电池时，应该使用2D轴对称模型，当压头是长条并且电池单元的宽度足够时，2D平面应变模型很合适。从理论上讲，3D完整模型可用于所有类型的加载条件（压头和加载方向的几何形状）。这三种类型的有限元模型都具有与输入相同的材料本构关系，唯一的区别在于代码类型。
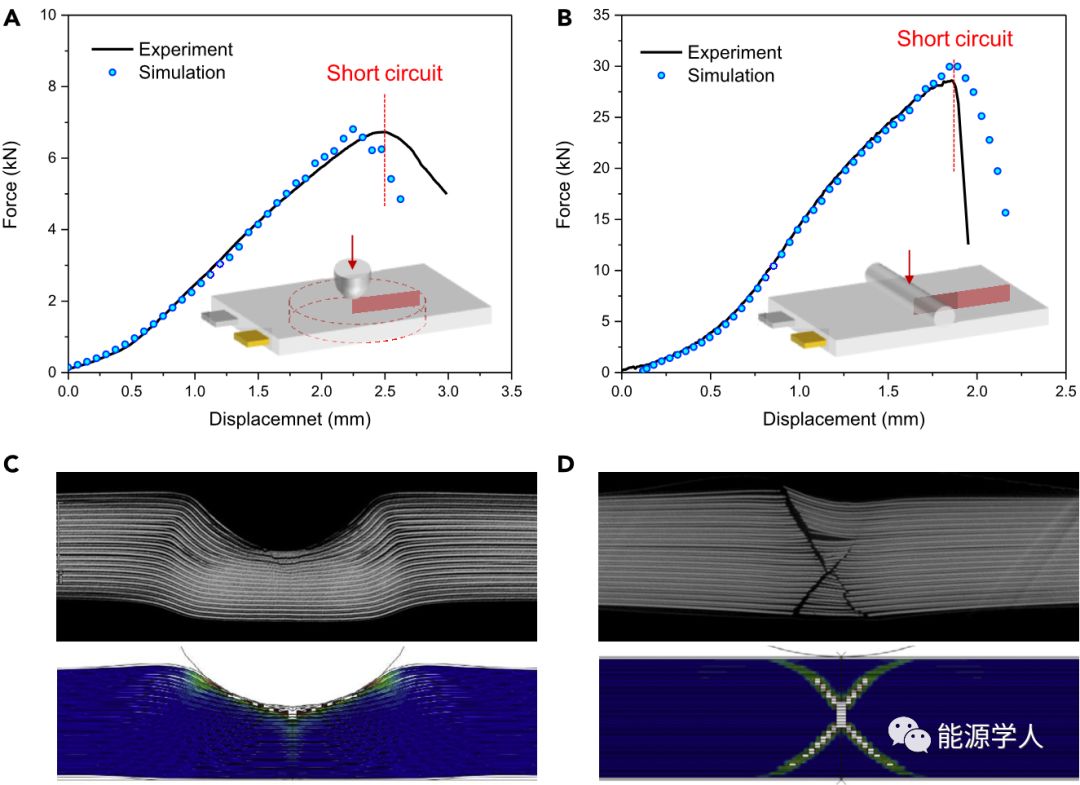
图2. 有限元模型完美适配了实验结果的两个重要方面，（A和B）力-位移响应；（C和D）断裂行为。研究了（A和C）压痕情况，即非球形压痕；（B和D）圆柱形压痕。在准静态加载条件下在电池水平上进行两次压痕测试作为有限元模型的验证。一个压头是一个半径为6.5毫米的半球，另一个是半径为15毫米的圆柱杆。测试装置和力-位移曲线分别如图2A和2B所示。通过电压下降来测量，发现峰值负载与发生短路一致。同时，利用二维轴对称模型和二维平面应变模型分别进行了数值模拟。模拟结果绘制在相同的坐标中进行比较。发现模拟和实验之间完美符合。如图2C和2D所示，通过高分辨率微CT扫描以检查测试电池单元的断裂模式。在半球形压痕试验中，变形局部化并且仅在表面附近的几层中发生断裂，而在圆柱形压痕中，观察到贯穿厚度的裂缝。两种情况都涉及隔膜失效直接导致短路。模拟结果成功预测了圆柱形压痕的“X形”裂缝。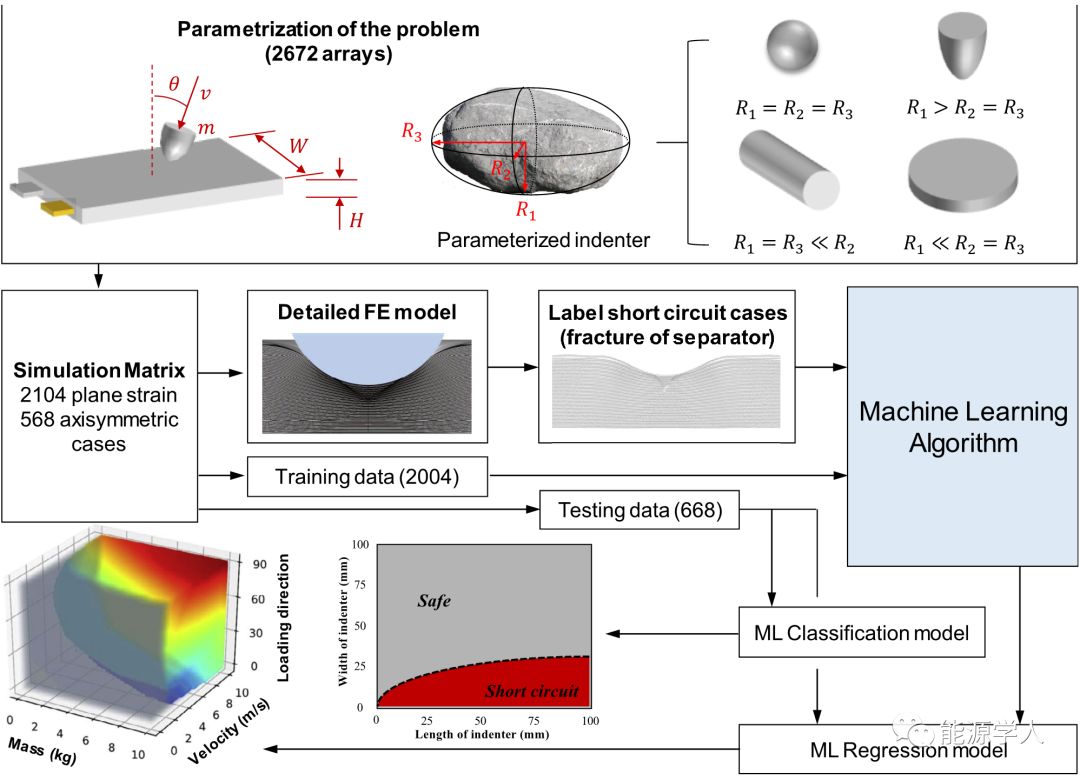
图3. 使用ML模型的数据驱动“安全范围“的流程图：进行了2672次数值模拟以生成ML模型的数据，使用隔膜断裂作为短路的标准。训练分类模型和回归模型。前者预测短路，后者预测压头的入侵导致短路。如图3所示，为了开发测试锂离子电池的数据驱动的安全范围，应该对该问题进行参数化。电池单元的几何形状由宽度W和厚度H表示。电池长度不予考虑，因为它通常大于宽度，因此不是机械安全的短板。加载角度为θ，加载速度为v，压头的质量为m。由于在现实的车祸中存在各种冲击对象，因此很难对压头的几何形状进行参数化，并且没有简单的方式描述所有可能的几何形状。在这项研究中，采用由R1，R2和R3定义的椭球刚性压头作为三个主轴的长度（见图3）。R1 = R2 = R4表示半球形压痕，R2 = R3 产生圆柱形压痕，R1 电池单元的面外压缩。如果材料特性和微观结构在不同电池之间变化，则会有更多参数。然而，本研究主要关注加载条件的影响，因此只研究了上述八个参数作为变量。然后设计了2672个阵列的模拟矩阵，其中包括2104个二维平面应变情况和568个2-D轴对称情况（见表S4）。在大型模拟矩阵中只考虑2D情况，因为它们比3D模拟具有更高的计算效率，所有案例中有四分之三用作某种ML算法的训练数据，而其余案例用作测试数据。通过Matlab代码实现了该标准的检测以及从Abaqus仿真到ML训练和数据处理。电池单元的“安全范围”由两个ML模型，一个分类模型和一个回归模型表征。前者可以快速判断给定的压头和负载条件是否会导致电池短路，后者定量地预测压头入侵，受力和动能引起的短路。两种模型均采用相同的数值模拟数据库进行独立训练。三种不同的ML算法，即决策树，支持向量机（SVM）和人工神经网络（ANN）用于分类，后两个用于回归。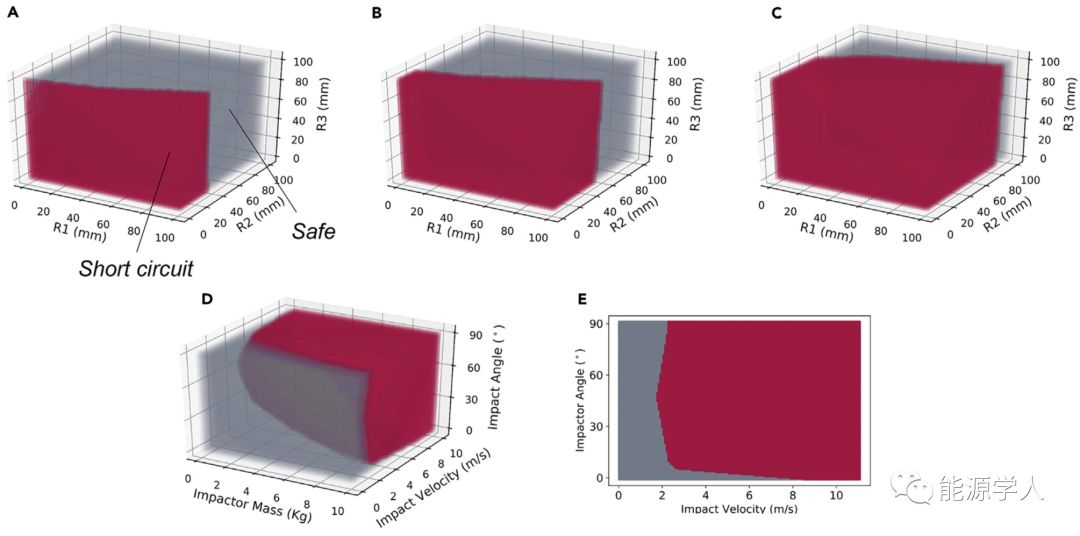
图4. 研究的锂离子电池单元的安全范围的分类模型由分类模型at m = 4kg，θ=90° 和不同速度产生的一组（R1，R2和R3）相图：（A） v = 4m/s，（B）6m/s，和（C）8m/s表明压头形状的安全和不安全范围。另一方面，在R1=R2=R3=6.35mm获得（m，v，θ）的相图（D）表示加载条件的影响，2D图（E）表示为m=10kg，显示加载角度的影响。理论上，所研究的锂离子电池的“安全范围“涉及八个参数。然而，可以看出机械响应对八个不同参数的灵敏度存在明显差异。首先，我们发现响应对电池单元的两个几何变量（厚度H，宽度W）的依赖性非常弱。实际上，这两个变量的值被限制在合理的范围内，即H通常为5-10mm，其为约20层的交替电极-隔膜单元，W约30-150mm。因此，它们被视为不敏感变量，以下安全范围将基于H = 6.72 mm和W = 30 mm。通过这种简化，问题只涉及六个高灵敏度的变量。一种方便实用的可视化方法是通过选择六个中的三个来实现3D“相图”。（R1，R2和R3）的相图绘制在图4A-4C中，固定质量m = 4kg，加载角θ = 90°，三种不同的速度（a）v = 4m / s，（b）6 m / s，和（c）分别为8 m / s。如果电池由于R1，R2和R3处于红色范围内的压头而变形，则会引起电短路。否则，它是机械安全的（灰色范围）。显然，尖锐的压头（R2小，R1和R3大）对电池比钝的更危险。随着加载速度的增加，短路范围变宽。因此高冲击能量对结构是危险的。图4D显示了R1 = R2 = R3 = 6.35mm处获得的示例图。得到一个明确的结论，当压头的冲击能量（mv2/2）很高时，更可能发生短路。在10kg的冲击质量下构建2D图（图4E），垂直载荷（90°）不一定是最关键的载荷方向。当冲击压痕发生在大约50°时，较小的速度（1.9 m/s）即可引起短路，而在90°时则需要2.2 m/s。该发现对于锂离子电池的安全性测试非常重要。预测锂离子电池单元的短路不能仅通过压头的固定单值标准，反应力或压头的动能来判断。因为短路的物理机制是阳极和阴极通过隔膜的断裂接触，这是一个复杂的过程，涉及隔膜的失效应变，整个电池的结构，所有的机械性能以及组件材料和边界条件。图5C和5F中结果的另一个结论是锂离子电池本身并不能很好的抵抗冲击，尤其当经受倾斜冲击载荷时。该结果强调了设计额外的防弹结构以吸收压头的重要性。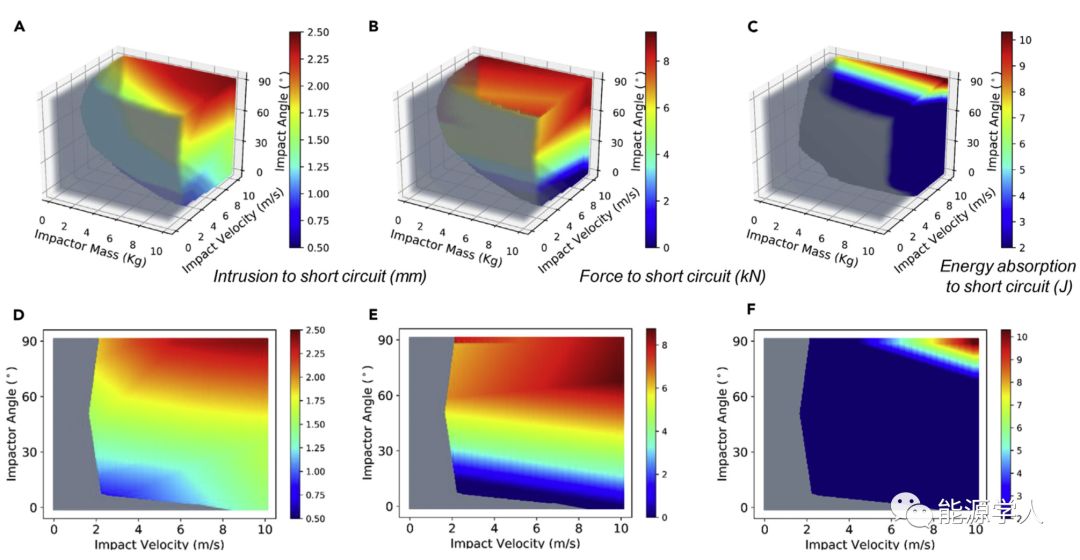
图5. 研究的锂离子电池单元的安全范围的回归模型：
（AC）基于图4D在R1=R2=R3=6.35mm处，“不安全”范围由（A）压头的侵入，（B）阻力和（C）能量吸收的轮廓指定。m = 10kg时，电池单元短路的2D曲线（D），（E）和（F）分别从（A），（B）和（C）获得，。电池技术的迅速发展使世界进入了电动汽车的新时代。然而，在这个新时代，行业正面临着
安全性的挑战。最紧迫的任务是确定电池单元安全运行的机械负载条件范围，称为“安全范围”。开发它需要大量的机械测试数据库，这是一项艰巨的挑战。本文通过采用软包电池的高精度有限元模型来克服这一挑战，生成超过2500个数值模拟结果并使用机器学习算法分析数据。该安全范围为EV和电池的设计提供了重要指导。Wei Li, Juner Zhu, Yong Xia, Maysam B. Gorji, Tomasz Wierzbicki Data-Driven Safety Envelope of Lithium-Ion Batteries for Electric Vehicles. Joule 2019 3, 1–13, doi.org/10.1016/j.joule.2019.07.026.
