
什么是决策树
决策树(Decision Tree)是一个非常容易理解的模型,它非常像我们所熟悉的if-then结构。举一个相亲见面的实例,即女生根据男生的条件来决定是否相亲见面,通过这个实例来简单理解决策树。
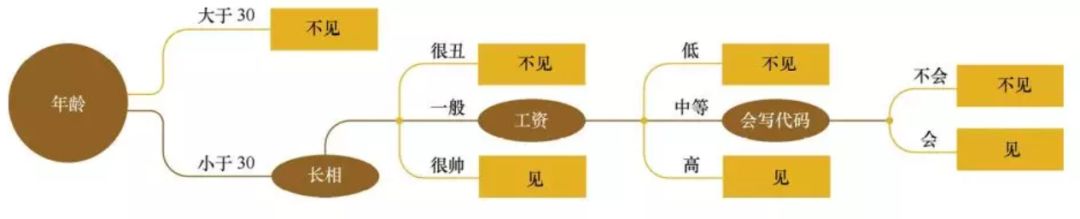
显而易见,决策树是一种自上而下,对样本数据进行树形分类的过程,有一个根结点、若干个内部结点和若干个叶结点组成。
决策树的构建过程
步骤一:将所有的特征看成一个一个的节点。
步骤二:遍历当前数据的每一种分割方式,找到最佳的分割点。
步骤三:使用第二步找到的最佳分割点进行划分,得出子节点N1、 N2….Nm。
步骤四:对子节点 N1、N2….Nm 分别继续执行 2-3 步,直到每个最终的子节点都足够“纯”(子结点中所包含的样本尽可能属于同一类别)。
从上述步骤可以看出,决策树算法的核心即是要解决两个问题:
决策树算法的 Python 实现
特征选择
特征选择就是决定用哪个特征来划分特征空间,其目的在于选取对训练数据具有分类能力的特征。那么如何来选择最佳的特征呢?
一般而言,随着划分过程不断进行,我们希望划分后得到的子结点中所包含的样本尽可能属于同一类别,即节点的纯度(purity)越来越高。在实际使用中,我们衡量的常常是不纯度。度量不纯度的指标有很多种,比如:信息熵、增益率、基尼系数。
信息熵
“信息熵” (information entropy) 是度量样本集合纯度最常用的一种指标。假定当前样本集合 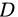 中第
中第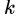 类样本所占的比例为
类样本所占的比例为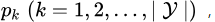 则
则 的信息熵定义为:
的信息熵定义为:
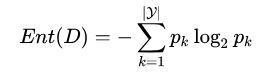
计算香农熵:
def calEnt(dataSet):
n = dataSet.shape[0]
iset = dataSet.iloc[:,-1].value_counts()
p = iset/n
ent = (-p*np.log2(p)).sum()
return ent
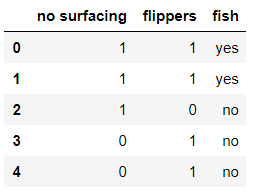
以书上的海洋生物数据为例,我们来构建数据集,并计算其香农熵:
import numpy as np
import pandas as pd
def createDataSet():
row_data = {'no surfacing':[1,1,1,0,0],
'flippers':[1,1,0,1,1
],
'fish':['yes','yes','no','no','no']}
dataSet = pd.DataFrame(row_data)
return dataSet
dataSet = createDataSet()
dataSet
信息增益
假设样本集 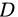 中某一离散属性
中某一离散属性 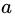 有
有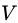 个可能的取值
个可能的取值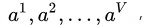 若使用
若使用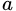 来对样本集
来对样本集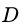 进行划分,则会产生
进行划分,则会产生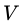 个分支结点 (注意:这里是默认把离散属性的每个可能的取值都进行划分),其中第
个分支结点 (注意:这里是默认把离散属性的每个可能的取值都进行划分),其中第 个分支结点包含了
个分支结点包含了 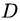 中所有在属性
中所有在属性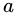 上取值为
上取值为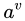 的样本,记为
的样本,记为 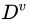 。我们可根据信息熵的定义计算出
。我们可根据信息熵的定义计算出 的信息熵。再考虑到不同分支结点所包含的样本数不同,给分支结点赋予权重
的信息熵。再考虑到不同分支结点所包含的样本数不同,给分支结点赋予权重 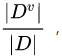 即样本数越多的分支结点的影响越大,于是可以计算出用属性
即样本数越多的分支结点的影响越大,于是可以计算出用属性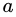 对样本集
对样本集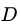 进行划分所获得的 “信息增益“ (information gain):
进行划分所获得的 “信息增益“ (information gain):
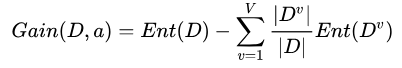
一般来说,信息增益越大,使用该特征划分所获得的“纯度提升”就越大,所以每次可以选择获得最大信息增益的特征来进行划分结点。 ID3 算法就是选择最大信息增益来划分结点的。
我们尝试手动计算下,海洋生物数据集中no surfacing列的信息增益:
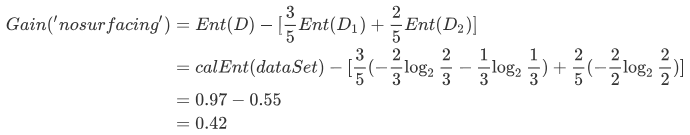
a=(3/5)*(-(2/3)*np.log2(2/3)-(1/3)*np.log2(1/3))
calEnt(dataSet)-a
用同样的方法,也可以把第 1 列的信息增益也算出来,结果为 0.17。
数据集的最佳切分
划分数据集的最大准则是选择最大信息增益,也就是信息下降最快的方向。
def bestSplit(dataSet):
baseEnt = calEnt(dataSet)
bestGain = 0
axis = -1
for i in range(dataSet.shape[1]-1):
levels= dataSet.iloc[:,i].value_counts().index
ents = 0
for j in levels:
childSet = dataSet[dataSet.iloc[:,i]==j]
ent = calEnt(childSet)
ents += (childSet.shape[0]/dataSet.shape[0])*ent
infoGain = baseEnt-ents
if (infoGain > bestGain):
bestGain = infoGain
axis = i
return axis
通过上面手动计算,可以得出,第 0 列的信息增益为 0.42,第 1 列的信息增益为 0.17,0.42 > 0.17,所以我们应该选择第 0 列进行切分数据集。也可以见证下我们构造的函数返回的结果是否和手动计算的一致:
bestSplit(dataSet)
0
按照给定列切分数据集
通过最佳切分函数返回最佳切分列的索引,我们就可以根据这个素引,构建一个按照给定列切分数据集的函数:
def mySplit(dataSet,axis,value):
col = dataSet.columns[axis]
redataSet = dataSet.loc[dataSet[col]==value,:].drop(col,axis=1)
return redataSet
递归构建决策树
构建决策树的算法有很多,比如 ID3、C4.5 和 CART,基于《机器学习实战》这本书,我们选择 ID3 算法。ID3 算法的核心是在决策树各个节点上对应信息增益准则选择特征,递归地构建决策树。具体方法是:从根节点开始,对节点计算所有可能的特征的信息增益,选择信息增益最大的特征作为节点的特征,由该特征的不同取值建立子节点;再对子节点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。
递归结束的条件是:程序遍历完所有的特征列或者每个分支下的所有实例都已经具有相同的分类。
def createTree(dataSet):
featlist = list(dataSet.columns) #提取出数据集所有的列
classlist = dataSet.iloc[:,-1].value_counts() #获取最后一列类标签
#判断最多标签数目是否等于数据集行数,或者数据集是否只有一列
if classlist[0]==dataSet.shape[0] or dataSet.shape[1] == 1
:
return classlist.index[0] #如果是,返回类标签
axis = bestSplit(dataSet) #确定出当前最佳切分列的索引
bestfeat = featlist[axis] #获取该索引对应的特征
myTree = {bestfeat:{}} #采用字典嵌套的方式存储树信息
del featlist[axis] #删除当前特征
valuelist = set(dataSet.iloc[:,axis]) #提取最佳切分列所有属性值
for value in valuelist: #对每一个属性值递归建树
myTree[bestfeat][value] = createTree(mySplit(dataSet,axis,value))
return myTree
查看函数运行结果:
myTree = createTree(dataSet)
myTree
使用决策树进行分类
def classify(inputTree,labels, testVec):
firstStr = next(iter(inputTree))
secondDict = inputTree[firstStr]
featIndex = labels.index(firstStr)
for key in secondDict.keys():
if
testVec[featIndex] == key:
if type(secondDict[key]) == dict :
classLabel = classify(secondDict[key], labels, testVec)
else:
classLabel = secondDict[key]
return classLabel
def acc_classify(train,test):
inputTree = createTree(train)
labels = list(train.columns)
result = []
for i in range(test.shape[0]):
testVec = test.iloc[i,:-1]
classLabel = classify(inputTree,labels,testVec)
result.append(classLabel)
test['predict']=result
acc = (test.iloc[:,-1]==test.iloc[:,-2]).mean()
print(f'模型预测准确率为{acc}')
return test
测试函数:
train = dataSet
test = dataSet.iloc[:3,:]
acc_classify(train,test)
sklearn中的决策树
sklearn中决策树的类都在tree这个模块之下。这个模块总共包含五个类:
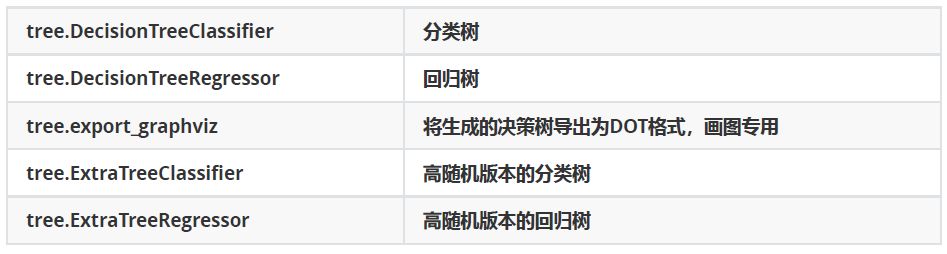
sklearn的基本建模流程:
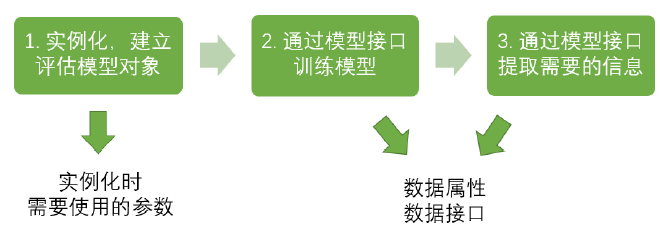
在这个流程下,分类树对应的代码是:
from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)
result = clf.score(X_test,y_test)
使用红酒数据集建树
from sklearn import tree
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
wine = load_wine()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
重要参数
criterion:这个参数用来决定不纯度的计算方法,包括信息熵(Entropy)和基尼系数(Gini Impurity)。默认为基尼系数。另外,因为信息熵对不纯度更加敏感,所以信息熵作为指标时,决策树的生长会更加“精细”,因此对于高维数据或者噪音很多的数据,信息熵很容易过拟合,基尼系数在这种情况下效果往往比较好,但也不是绝对的。
splitter
:特征划分标准,可选 best或random。best在特征的所有划分点中找出最优的划分点,random随机的在部分划分点中找局部最优的划分点。默认的best适合样本量不大的时候,而如果样本数据量非常大,此时决策树构建推荐random。
剪枝参数
max_depth:决策树最大深度,超过设定深度的树枝全部剪掉。默认值是None。一般数据比较少或者特征少的时候可以不用管这个值,如果模型样本数量多,特征也多时,推荐限制这个最大深度,具体取值取决于数据的分布。常用的可以取值10-100之间,常用来解决过拟合。
min_samples_split:内部节点(即判断条件)再划分所需最小样本数。默认值为 2。如果是 int,则取传入值本身作为最小样本数;如果是 float,则取ceil(min_samples_split*样本数量)作为最小样本数。(向上取整)
min_samples_leaf:叶子节点(即分类)最少样本数。如果是 int,则取传入值本身作为最小样本数;如果是 float,则取ceil(min_samples_leaf*样本数量)的值作为最小样本数。这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。
max_features & min_impurity_decrease:max_features限制分枝时考虑的特征个数,超过限制个数的特征都会被舍弃。max_features是用来限制高维度数据的过拟合的剪枝参数,但其方法比较暴力,是直接限制可以使用的特征数量而强行使决策树停下的参数,在不知道决策树中的各个特征的重要性的情况下,强行设定这个参数可能会导致模型学习不足。如果希望通过降维的方式防止过拟合,建议使用 PCA,ICA 或者特征选择模块中的降维算法。min_impurity_decrease限制信息增益的大小,信息增益小于设定数值的分枝不会发生。
score_train = clf.score(Xtrain, Ytrain)
score_train
示例:使用超参数的学习曲线确认最优的剪枝参数
超参数的学习曲线,是一条以超参数的取值为横坐标,模型的度量指标为纵坐标的曲线,它是用来衡量不同超参数取值下模型的表现的线。在我们建好的决策树里,我们的模型度量指标就是score。
import matplotlib.pyplot as plt
test = []
for i in range(10):
clf = tree.DecisionTreeClassifier(max_depth=i+1
,criterion="entropy"
,random_state=30
,splitter="random"
)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
test.append(score)
plt.plot(range(1,11),test,color="red",label="max_depth")
plt.legend()
plt.show()
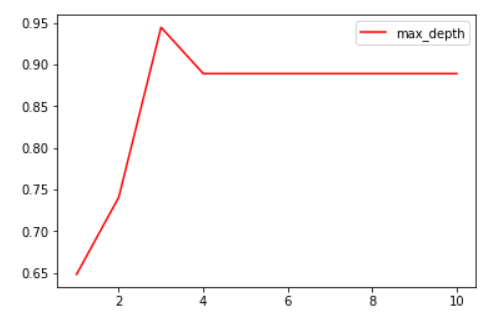
由max_depth的学习曲线可得,在max_depth=3时模型最佳。
决策树的优缺点
猜你喜欢
机器学习实战 | k-邻近算法
一起来学习机器学习吧~
生信基础知识100讲
生信菜鸟团-专题学习目录(5)
还有更多文章,请移步公众号阅读
▼ 如果你生信基本技能已经入门,需要提高自己,请关注下面的生信技能树,看我们是如何完善生信技能,成为一个生信全栈工程师。

▼ 如果你是初学者,请关注下面的生信菜鸟团,了解生信基础名词,概念,扎实的打好基础,争取早日入门。
