来源:投稿 作者:Fairy
编辑:学姐
在机器学习算法中,数据距离是一个核心概念,它衡量了数据点之间的差异或相似度。不同的数据距离度量方法适用于不同的场景和问题,选择合适的距离度量方式对于算法的性能和效果有着至关重要的影响。
本文将深入探讨机器学习算法中的五种常见数据距离:欧氏距离、标准化欧氏距离、切比雪夫距离、马氏距离和闵氏距离,并通过Python代码利用常见数据集计算这些距离。
一、欧氏距离
1. 公式与原理
欧氏距离是最常用的距离度量方法之一,它衡量的是多维空间中两点之间的直线距离。在二维空间中,欧氏距离可以通过勾股定理来计算。对于两个n维向量x=(x1, x2, ..., xn)和y=(y1, y2, ..., yn),欧氏距离d(x, y)的计算公式为:
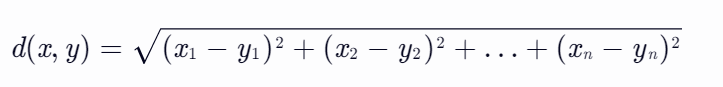
这个公式可以理解为在n维空间中将两点间的直线段视为一个n维超直角三角形的斜边,而每个维度上的差值(xi - yi)则是其他边的长度。
2. 应用场景
- 聚类分析:在K-Means算法中,欧氏距离用于计算样本点与质心之间的距离,以确定样本点的归属。
- 分类任务:在K-最近邻(K-NN)算法中,使用欧氏距离来识别最近的邻居,进而进行分类或回归。
- 计算几何:欧氏距离用来计算点、线、面之间的最短距离,是基本的几何计算。
- 图像处理:欧氏距离可以用来衡量像素点之间的颜色差异,以进行颜色量化或者图像分割。
- 物理学:欧氏距离可以用来计算两个物体之间的实际距离,这在许多物理公式和模型中是基本的参数。
3. Python代码示例
下面是一个使用Python计算欧氏距离的示例代码:
import numpy as np
def euclidean_distance(p1, p2):
return np.sqrt(np.sum((p1 - p2) ** 2))
# 示例数据点
p1 = np.array([1, 2, 3])
p2 = np.array([4, 5, 6])
distance = euclidean_distance(p1, p2)
print(f"Euclidean distance between p1 and p2: {distance}")
二、标准化欧氏距离
1. 公式与原理
标准化欧氏距离是对简单欧氏距离的改进,它通过将数据各维分量均值归一化到0,方差归一化到1来消除分布差异。标准化欧氏距离的计算公式为:
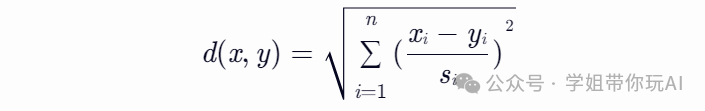
其中,si是第i维分量的标准差。这个公式可以看作是一种加权欧氏距离,其中权重是各维分量标准差的倒数。
2. 应用场景
标准化欧氏距离常用于处理特征量纲不同或分布差异较大的数据。例如,在基因表达数据分析中,不同基因的表达量可能具有不同的量纲和分布,使用标准化欧氏距离可以更准确地衡量不同样本间的表达模式差异。
3. Python代码示例
下面是一个使用Python计算标准化欧氏距离的示例代码:
import numpy as np
def standardized_euclidean_distance(p1, p2, means, stds):
return np.sqrt(np.sum(((p1 - means) / stds - (p2 - means) / stds) ** 2))
# 示例数据点
p1 = np.array([1, 2, 3])
p2 = np.array([4, 5, 6])
# 假设各维分量的均值和标准差
means = np.array([2, 3, 4])
stds = np.array([1, 1, 1])
distance = standardized_euclidean_distance(p1, p2, means, stds)
print(f"Standardized Euclidean distance between p1 and p2: {distance}")
三、切比雪夫距离
1. 公式与原理
切比雪夫距离也称为棋盘距离,它衡量的是两点之间的最大坐标差。在数学中,切比雪夫距离(Chebyshev distance)或是L∞度量,是向量空间中的一种度量。对于两个n维向量x=(x1, x2, ..., xn)和y=(y1, y2, ..., yn),切比雪夫距离d(x, y)的计算公式为:
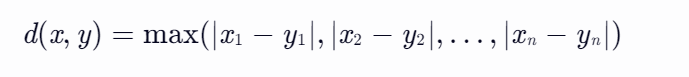
这个公式可以理解为在国际象棋中,国王从一个位置走到另一个位置所需的最小步数(因为国王可以横向、纵向或斜向移动一格)。
2. 应用场景
-
图像处理:切比雪夫距离用于比较两个图像的相似程度。
- 聚类分析:切比雪夫距离被用来衡量不同对象之间的差异。
- 无线通信:在无线通信中,信号的覆盖范围经常被描述为一个正方形(对于无线电视塔或其他传输设备),其中的距离度量经常使用切比雪夫距离。
3. Python代码示例
下面是一个使用Python计算切比雪夫距离的示例代码:
def chebyshev_distance(p1, p2):
return np.max(np.abs(p1 - p2))
# 示例数据点
p1 = np.array([1, 2, 3])
p2 = np.array([4, 5, 6])
distance = chebyshev_distance(p1, p2)
print(f"Chebyshev distance between p1 and p2: {distance}")
四、马氏距离
1. 公式与原理
马氏距离是一种受协方差影响的距离测量方式,在统计学和机器学习中广泛应用。它的基本思想是,通过考虑各个特征之间的差异和变异,来计算两个样本之间的相似度或距离。与欧氏距离不同的是,马氏距离会考虑特征之间的关联性。对于两个n维向量x和y,马氏距离dM(x, y)的计算公式为:
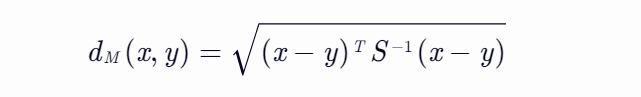
其中,S是x和y的协方差矩阵,S^(-1)是协方差矩阵的逆矩阵。协方差矩阵描述了数据特征之间的相关性,而逆矩阵则用于考虑数据在各个特征上的差异性。
2. 应用场景
- 特征选择:在特征选择中,马氏距离可以用来衡量不同特征之间的关联性,从而帮助选择更具代表性的特征。
- 异常检测:在异常检测中,马氏距离可以用来衡量数据点与数据集中心点的距离,从而识别出偏离正常模式的异常点。
- 分类任务:在某些分类任务中,马氏距离可以用来衡量样本点与类别中心的距离,从而进行分类。
3. Python代码示例
下面是一个使用Python计算马氏距离的示例代码:
import numpy as np
def mahalanobis_distance(p1, p2, cov_matrix):
inv_cov = np.linalg.inv(cov_matrix)
diff = p1 - p2
return np.sqrt(np.dot(np.dot(diff.T, inv_cov), diff))
# 示例数据点
p1 = np.array([1, 2])
p2 = np.array([4, 5])
# 假设协方差矩阵
cov_matrix = np.array([[2, 1], [1, 2]])
distance = mahalanobis_distance(p1, p2, cov_matrix)
print(f"Mahalanobis Distance between p1 and p2: {distance}")
五、闵氏距离
1. 公式与原理
闵氏距离,它不仅仅是一种距离,而是将多个距离公式(曼哈顿距离、欧式距离、切比雪夫距离)总结成为的一个公式。对于两个n维变量x=(x1, x2, ..., xn)和y=(y1, y2, ..., yn),闵氏距离d(x, y)的计算公式为:
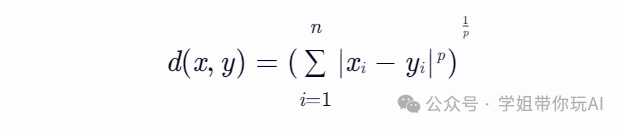
其中,p是一个变参数。当p取不同的值时,闵氏距离可以表示不同类型的距离:
- 当 p=1 时,闵氏距离等同于曼哈顿距离(Manhattan Distance),即各维度上坐标数值差的绝对值之和。
- 当 p=2 时,闵氏距离就是欧氏距离(Euclidean Distance),即各维度上坐标数值差的平方和的平方根。
- 当 p→∞ 时,闵氏距离趋近于切比雪夫距离(Chebyshev Distance),即各维度上坐标数值差的最大值。
闵氏距离的灵活性使其能够根据不同的应用场景和需求调整距离计算的敏感度,从而更准确地反映数据点之间的相似性或差异性。
2. 应用场景
- 多维数据分析:在多维数据分析中,闵氏距离可以用于计算数据点之间的综合距离,帮助识别数据的聚类结构或异常点。
- 机器学习算法:在K-最近邻(K-NN)、支持向量机(SVM)等机器学习算法中,闵氏距离可以作为距离度量函数,通过调整参数p来优化算法性能。
- 经济学和金融学:在经济学和金融学中,闵氏距离可以用于计算不同资产或市场指数之间的相似性或差异性,为投资决策提供依据。
- 图像处理和计算机视觉:在图像处理和计算机视觉领域,闵氏距离可以用于图像匹配、目标检测和识别等任务中,通过调整参数p来适应不同的图像特征和应用场景。
3. Python代码示例
下面是一个使用Python计算闵氏距离的示例代码,其中p作为参数可以灵活调整:
import numpy as np
def minkowski_distance(p1, p2, p):
return np.sum(np.abs(p1 - p2) ** p) ** (1 / p)
# 示例数据点
p1 = np.array([1, 2, 3])
p2 = np.array([4, 5, 6])
# 设置p值
p = 3 # 例如,这里使用p=3来计算闵氏距离
distance = minkowski_distance(p1, p2, p)
print(f"Minkowski Distance (p={p}) between p1 and p2: {distance}")
在这个示例中,我们通过设置不同的p值来计算不同类型的闵氏距离。当p=1时,结果等同于曼哈顿距离;当p=2时,结果等同于欧氏距离;当p趋近于无穷大时,结果趋近于切比雪夫距离(实际上,在编程中我们无法直接设置p为无穷大,但可以通过选择非常大的数值来近似)。
六、小结
通过理解这些距离的定义和特性,我们可以更好地选择适合特定问题的距离度量方法,从而提高机器学习算法的性能和效果。
在实际应用中,选择哪种距离度量方法取决于数据的性质、问题的需求和算法的特性。例如,如果数据各维分量的量纲和分布差异较大,可以考虑使用标准化欧氏距离;如果数据特征之间存在相关性,可以考虑使用马氏距离;如果需要灵活调整距离计算的敏感度,可以考虑使用闵氏距离。
最后,我们通过Python代码示例展示了如何计算这些距离。这些代码可以作为基础,根据实际需求进行扩展和修改。