一、引言
大家好,我是 Ai 学习的章北海
reddit 机器学习社区刷到一个有意思的话题
对使用降维技术来探索数据关系时,"降维会导致信息损失"的事儿讨论十分火热。

二、降维与特征选择的深度对比
2.1 特征选择的优势
特征选择是一种更为直观的维度处理方法。当我们面对具有明确业务含义的表格数据时,特征选择表现出独特的优势:
可解释性保持:例如在金融数据分析中,"租金"和"工资"这样的特征具有明确的业务含义。通过特征选择,我们可以保留这些关键指标的原始含义,使模型结果更容易向业务人员解释。
精确的特征筛选:特征选择允许我们基于领域知识和统计指标(如方差、相关性)来精确删除噪声特征,而不是对所有特征进行变换。
2.2 降维技术的特点
降维技术通过数学变换将高维数据映射到低维空间,这一过程具有双面性:
信息压缩:以 PCA 为例,它通过寻找数据的主成分,将原始特征组合成新的、正交的特征。这种变换可能会将"租金"和"工资"这样的特征合并成一个抽象的"经济能力"维度。值得注意的是,PCA 的优势在于它能创建一个有序的特征空间,其中轴线按解释方差排序,并且与原始特征的关系是明确且有意义的。
隐藏模式发现:降维技术能够发现数据中的潜在结构。例如,t-SNE 在处理高维文本数据时,能够揭示出文本之间的语义关系,这是单纯的特征选择难以实现的。然而,这些方法的有效性很大程度上取决于特征的运动是否由少数潜在因子驱动。即使存在这种情况,这些方法也不一定能完全清晰地恢复这些因子。
2.3 因果系的考虑
在进行特征选择时,还需要考虑特征之间的因果关系:
- 共同因素分析:相关特征可能存在或不存在共同影响因素(confounding factors)
- 因果建模:了解特征间的因果关系可以帮助优化建模设计
- 目标导向:特征间的关系建模与特征与目标变量关系的建模是不同的目标,使用错误的目标函数可能导致次优结果
三、降维技术的适用场景分析
3.1 不适合使用降维的情况
- 特征间的相关性(PCA 捕获的)可能与预测任务无关
- 实例:在预测房价时,将"房屋面积"和"地理位置"降维可能会损失这两个特征对房价的独特影响
- 在需要向非技术 stakeholders 解释模型决策时
3.2 推荐使用降维的场景
- 实例:将 1000 维的词向量降至 2-3 维进行文本聚类可视化
- 实例:在线推荐系统中,可以通过降维减少用户特征的存储和计算开销
- 实例:使用 t-SNE 可视化深度学习模型中间层的特征分布
四、替代方案与最佳实践
4.1 高维数据分析的替代方法
- 使用 HSIC(Hilbert-Schmidt Independence Criterion)等方法直接测试高维变量间的依赖关系
- 特别适用于需要理解高维随机变量对之间相关性(甚至非线性依赖)的场景
- 这些方法本身也可以被视为一种降维分析,但它们更专注于变量间的对齐关系
4.2 实践建议
五、代码实例演示:降维技术在乳腺癌数据集上的应用
在前面的章节中,我们讨论了降维技术的理论基础、适用场景和最佳实践。现在,让我们通过一个实际的案例来展示如何在实践中应用这些知识。
5.1 问题背景
乳腺癌是全球女性最常见的癌症之一,早期诊断对于提高治愈率至关重要。医学研究人员收集了大量与乳腺癌相关的特征数据,这些高维数据包含了肿瘤的各种物理特性。我们将探索如何通过降维技术来分析这些数据,并评估不同方法的效果。
时间就是金钱,一杯咖啡,交个朋友
订阅后您将获得:
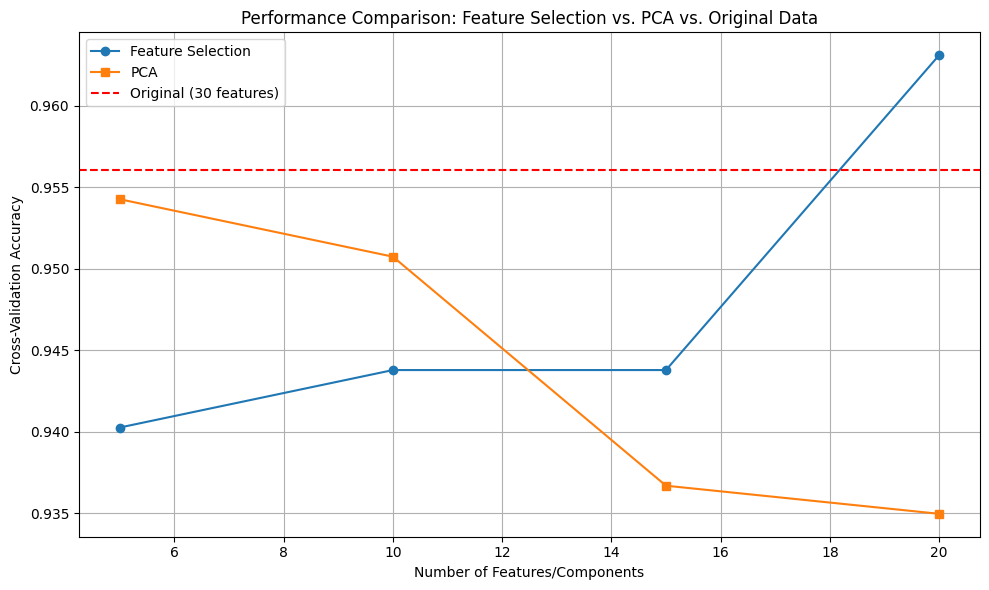
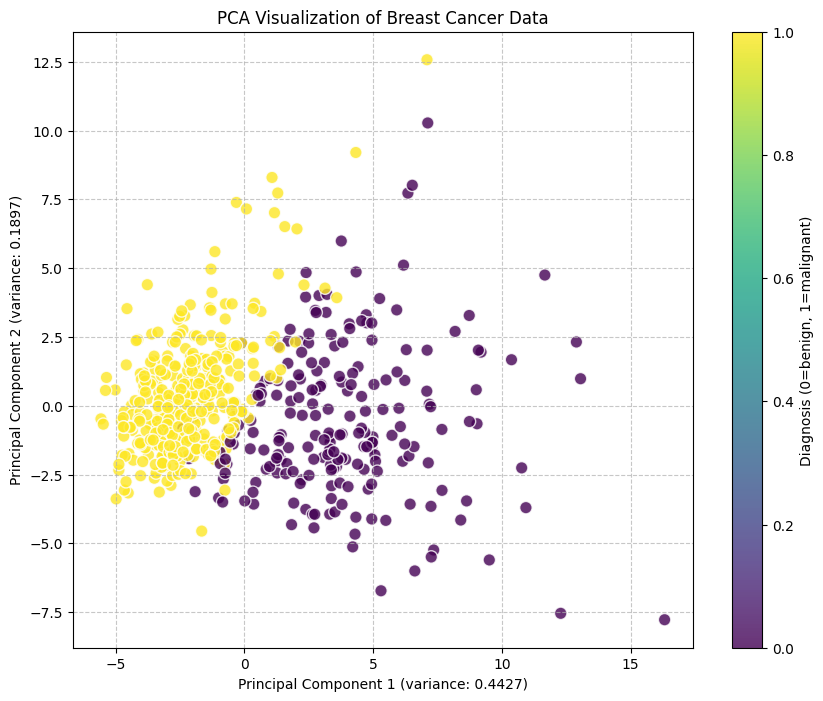
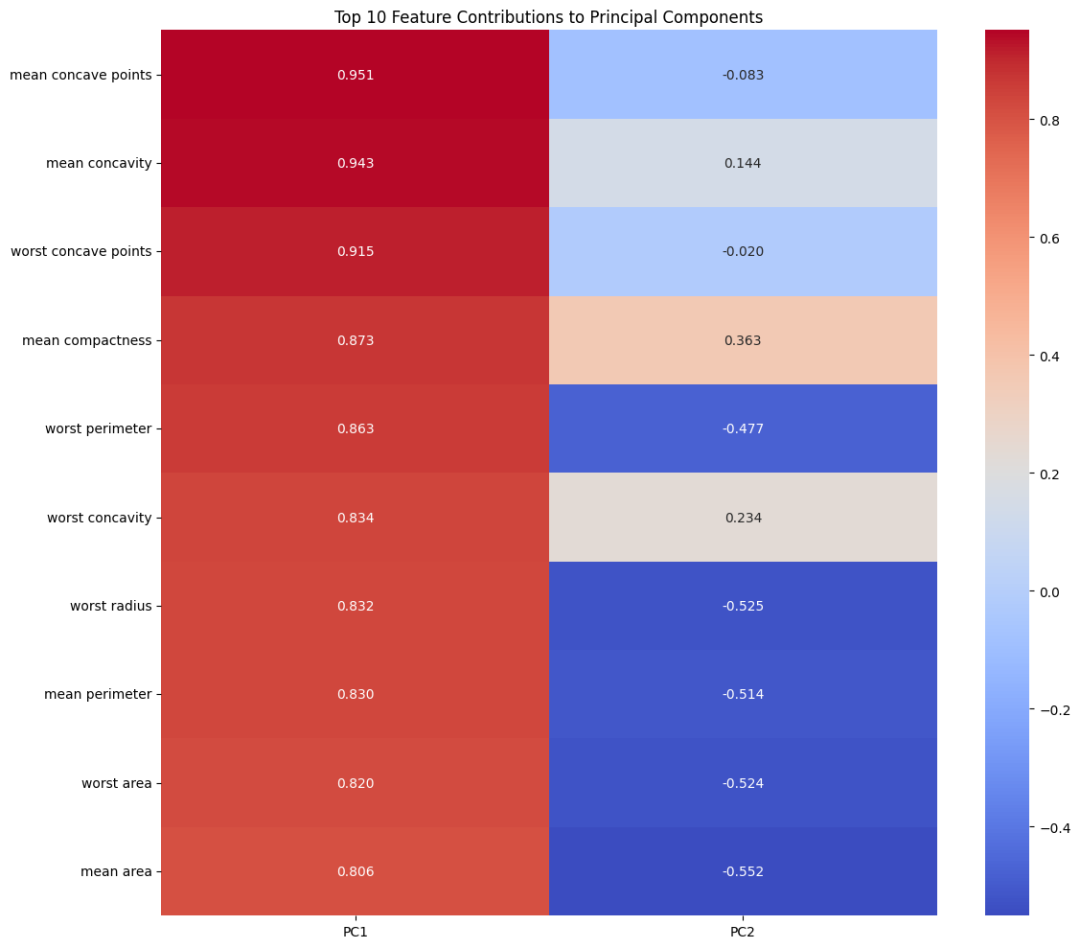
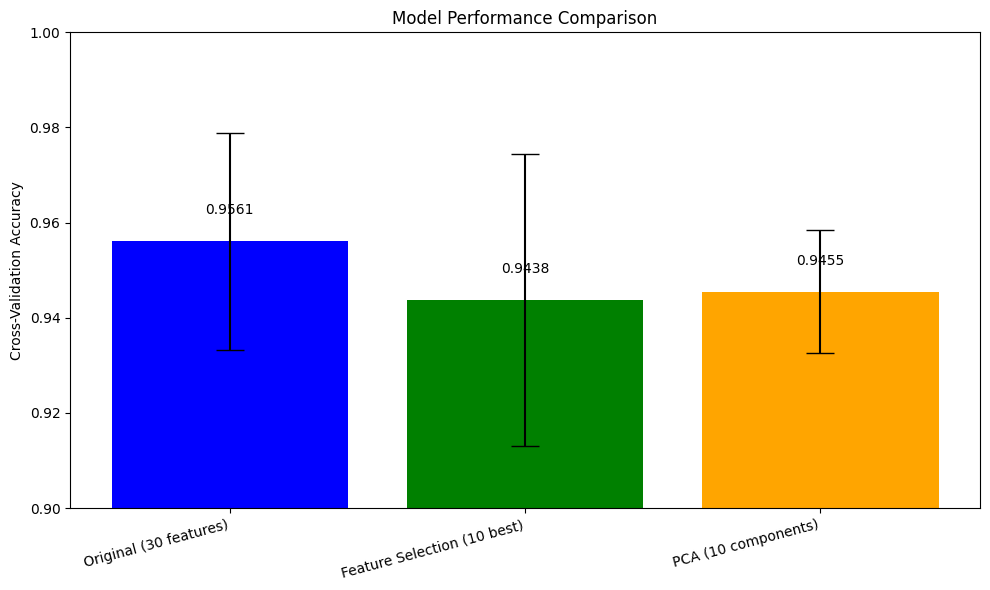
5.2 数据集介绍