
梯度下降(Gradient Descent,简称GD)是一种迭代式一阶优化算法,用于寻找给定函数的局部最小值或最大值。
在机器学习(Machine Learning)和深度学习(Deep Learning)中,该算法常用于最小化成本/损失函数(例如线性回归中)。
由于其重要性和易于实现的特点,该算法通常是几乎所有机器学习教程的入门教学内容。
而且梯度下降的应用不仅限于ML/DL领域,它还广泛应用于控制工程(如机器人、化工等领域)、计算机游戏、机械工程等领域。
本文将深入探讨一阶梯度下降算法的数学原理、实现方式和行为特性。
梯度下降算法由奥古斯丁·路易斯·柯西(Augustin-Louis Cauchy)于1847年提出,远早于现代计算机时代。
自那时以来,计算机科学和数值方法取得了显著发展,从而催生了众多改进的梯度下降版本,不过在本文中,我们将使用Python实现它的原始版本。
函数要求
梯度下降算法并不适用于所有函数,它有两个特定要求:
可微性意味着函数在其定义域内的每个点都有导数——并非所有函数都满足这一条件。
我们先来看一些满足这一条件的函数示例:
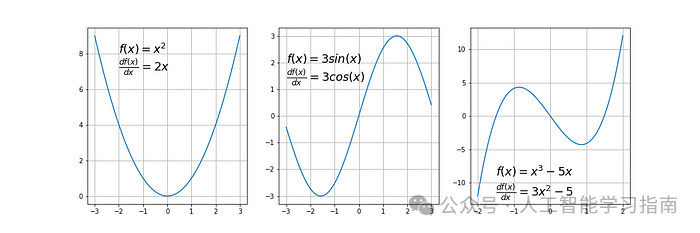
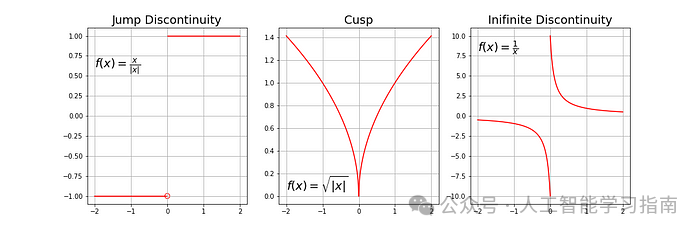
典型的不可微函数具有阶梯状、尖点或间断性。
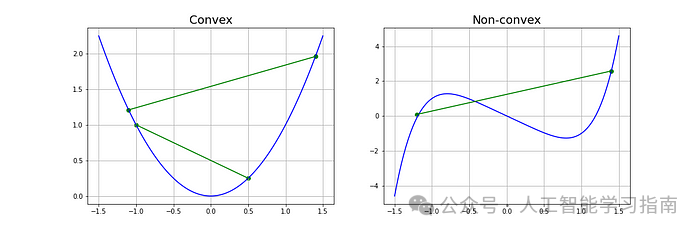
另一个要求是函数必须是凸函数,对于单变量函数而言,这意味着连接函数上两点的线段位于其曲线之上或与其重合(不穿过曲线)。
如果穿过,则意味着该函数具有局部最小值而非全局最小值。
从数学上讲,对于位于函数曲线上的两点x₁和x₂,这一条件可表示为:
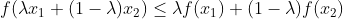
其中,λ 表示点在截面线上的位置,其取值范围必须在0(左端点)到1(右端点)之间,例如,λ=0.5 表示中点位置。
下面给出了两个带有示例截面线的函数。
另一种检查单变量函数是否为凸函数的方法是计算其二阶导数,并检查其值是否始终大于0。
让我们来看一个简单的例子(注意:接下来将涉及微积分):
一个简单二次函数:
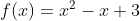
其一阶导数和二阶导数分别为:
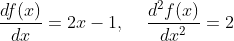
由于二阶导数始终大于0,所以我们的函数是严格凸函数。
虽然梯度下降算法也可以使用拟凸函数,但它们通常具有所谓的鞍点(也称为极小极大点),算法可能会在这些点处停滞(后文中会有演示)。拟凸函数的一个示例是:
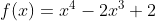
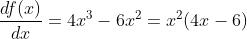
我们看到,该函数在x=0和x=1.5处的一阶导数为零,因此这些点是函数极值(最小值或最大值)的候选点——在这些点处斜率为零。但首先,我们必须检查二阶导数。
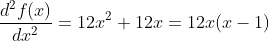
该表达式的值在x=0和x=1处为零,这些位置称为拐点——即曲率改变符号的点——意味着从凸变为凹或反之。
通过分析该方程,我们得出以下结论:
当x<0时,函数是凸的。
当0
当x>1时,函数再次变为凸的。
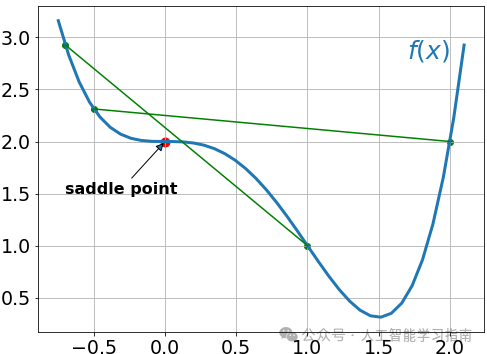
现在我们看到,点x=0处的一阶导数和二阶导数都为零,意味着这是一个鞍点,而点x=1.5是全局最小值。
让我们看一下该函数的图像。如前所述,鞍点位于x=0,最小值位于x=1.5。
对于多变量函数,检查某点是否为鞍点的最合适方法是计算Hessian矩阵,但这涉及更复杂的计算,所以我们不做讨论。
下图展示了双变量函数中的鞍点示例。

梯度
在编写代码之前,还有一件事需要解释——什么是梯度,直观地讲,梯度是指在给定点的指定方向上曲线的斜率。
对于单变量函数,它就是在选定点的一阶导数,对于多变量函数,它是在每个主要方向(沿变量轴)上的导数向量。
因为我们只关心一个轴上的斜率,而不关心其他轴,所以这些导数被称为偏导数。
对于n维函数f(x)在给定点p的梯度定义如下:
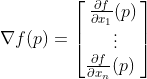
倒三角符号是所谓的nabla符号,读作“del”。为了更好地理解如何计算梯度,让我们对下面这个示例性的二维函数进行手工计算。
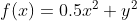
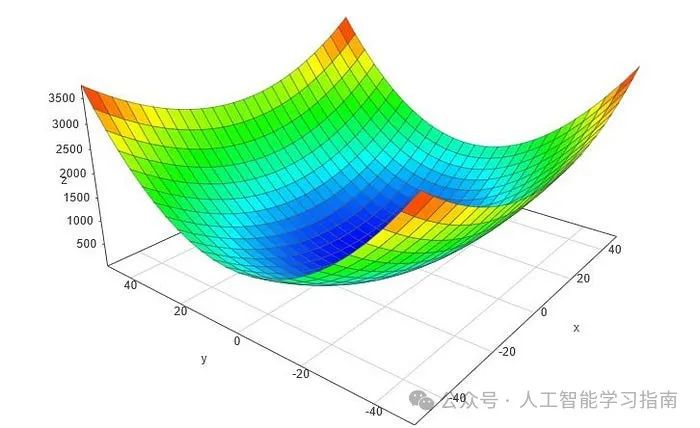
假设我们对点p(10,10)处的梯度感兴趣:
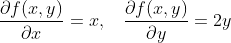
因此,结果如下:
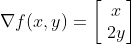
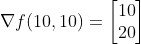
通过查看这些值,我们得出结论,沿y轴的斜率比沿x轴陡两倍。
梯度下降算法
梯度下降算法通过在当前位置使用梯度迭代计算下一个点,将其乘以一个学习率(进行缩放),并从当前位置减去所得值(即迈出一步)。
之所以减去该值,是因为我们希望最小化函数(若要最大化,则应加上该值)。该过程可以表示为:
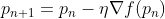
其中,有一个重要参数η,它用于缩放梯度,从而控制步长,在机器学习中,它被称为学习率,对性能有很大影响。
综上所述,梯度下降方法的步骤包括:
选择一个起始点(初始化);
在该点计算梯度;
沿与梯度相反的方向迈出缩放后的一步(目标:最小化);
重复步骤2和3,直到满足以下条件之一:
达到最大迭代次数。
步长小于容差(由于缩放或小梯度)。
下面是一个梯度下降算法的示例实现(带步骤跟踪):
import numpy as npfrom typing import Callable def gradient_descent(start: float, gradient: Callable[[float], float], learn_rate: float, max_iter: int, tol: float = 0.01): x = start steps = [start] for _ in range(max_iter): diff = learn_rate * gradient(x) if np.abs(diff) < tol: break
x = x - diff steps.append(x) return steps, x
该函数包含5个参数:
起始点[浮点数]——在本例中,我们手动定义它,但在实际应用中,它通常是随机初始化的
梯度函数[对象]——用于计算梯度的函数,该函数需提前指定并传递给梯度下降(Gradient Descent,简称GD)函数
学习率[浮点数]——步长的缩放因子
最大迭代次数[整数]
容差[浮点数],用于条件性地停止算法(本例中默认值为0.01)
示例1——二次函数
我们以一个简单的二次函数为例,定义如下:
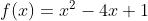
由于是单变量函数,其梯度函数为:
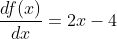
接下来,我们在Python中编写这些函数:
def func1(x:float): return x**2-4*x+1def gradient_func1(x:float): return 2*x - 4
对于此函数,当学习率设为0.1且起始点为x=9时,我们可以轻松手动计算每一步,让我们来计算前3步:
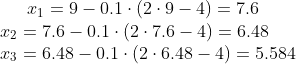
调用Python函数的命令为:
history, result = gradient_descent(9, gradient_func1, 0.1, 100)
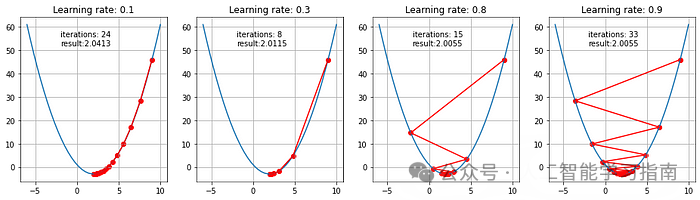
下面的动画展示了学习率为0.1和0.8时,GD算法所采取的步骤,可以看出,对于较小的学习率,随着算法接近最小值,步长逐渐减小。
而对于较大的学习率,算法在收敛前会在两侧来回跳跃。

不同学习率下的轨迹、迭代次数和最终收敛结果(在容差范围内)如下所示:
示例2——含有鞍点的函数
现在,让我们看看算法将如何处理我们之前在数学上研究过的半凸函数。
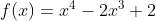
以下是两个学习率和两个不同起始点的结果。
以下是学习率为0.4且起始点为x=-0.5时的动画。
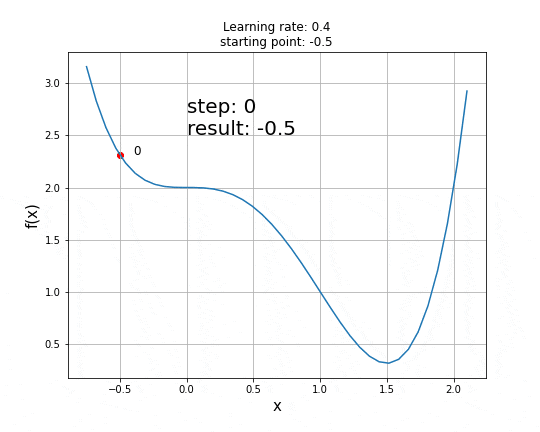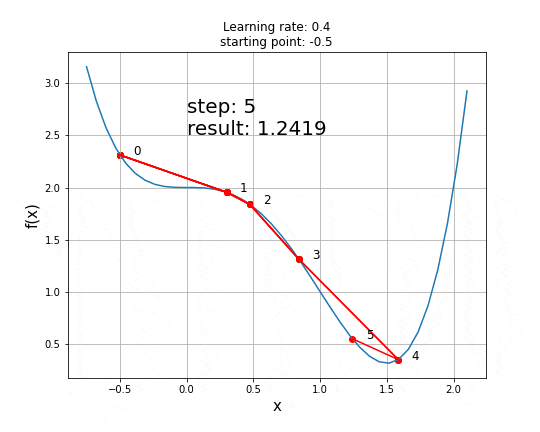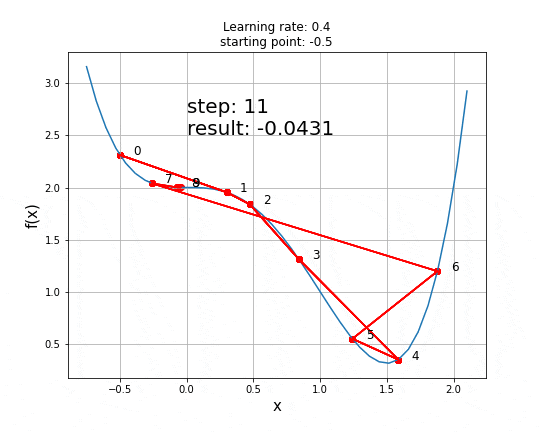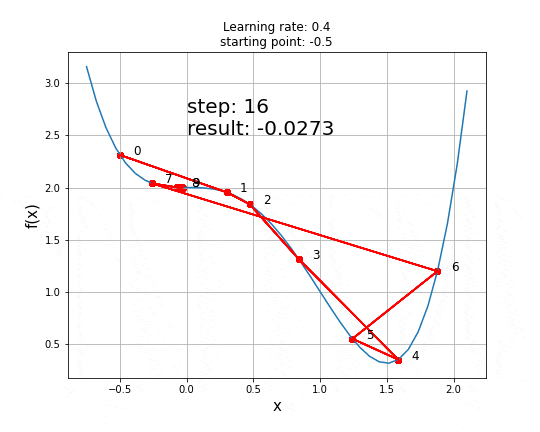
可以看到,鞍点的存在给GD等一阶梯度下降算法带来了真正的挑战,且无法保证获得全局最小值,二阶算法能更好地处理这些情况。
另外我们精心打磨了一套基于数据与模型方法的
AI科研入门学习方案(已经迭代过5次),对于人工智能来说,任何专业,要处理的都只是实验数据,所以我们根据实验数据将课程分为了三种方向的针对性课程,包含时序、图结构、影像三大实验室,我们会根据你的数据类型来帮助你选择合适的实验室,根据规划好的路线学习 只需 5 个月左右(很多同学通过学习已经发表了 sci 二区及以下、ei会议等级别论文)学习形式为 直播+ 录播,多位老师为你的论文保驾护航,如果需要发高区也有其他形式。
还有图结构、影像两个实验室(根据你的数据类型来选择)
大家感兴趣可以直接添加小助手微信:ai0808q 通过后回复咨询既可!
AI for science
大家想自学的我还给大家准备了一些机器学习、深度学习、神经网络资料大家可以看看以下文章(文章中提到的资料都打包好了,都可以直接添加小助手获取)
大家觉得这篇文章有帮助的话记得分享给你的死党、闺蜜、同学、朋友、老师、敌蜜!