【机器学习】讲透一个强大算法模型，Prophet！！

一直以来，都断断续续的会给大家分享有关时间序列的模型，以及一些常用方法。

今天，咱们分享的Prophet是非常好用且效果不错的一个模型，Prophet最初是由Facebook 开发，用来帮助预测数据的未来趋势。简单来说，时间序列预测就是通过分析历史数据，猜测未来会发生什么。比如你有过去几年每天的销售额数据，想预测明年的销售额趋势，Prophet 就是用来做这个的工具。

咱们简单的来解释一下Prophet~

理解历史数据的趋势：假设你想知道接下来几个月的销售额会怎么样，Prophet 首先会分析过去的数据，看有没有什么长期趋势，比如你的销售额是不是一年比一年增加，或者有时是减少的。
找出季节性变化：Prophet 还会查看有没有周期性的规律，比如每年夏天销售额会高一点，或者每周的周末销售比平时好。这样，它能识别出这些周期性的波动。
添加假期影响：如果你的数据里有节假日，Prophet 也能考虑进去，比如圣诞节期间销售额通常会暴涨，工具会识别出这种假期效应，做出更精准的预测。
预测未来趋势：综合这些信息后，Prophet 会根据已经找到的模式，推测未来会是什么样的趋势，比如未来几个月的销售额大概会怎么变化。

Prophet 的优点

简单好用：即使你不是数据科学专家，Prophet 也比较容易上手。你只需要提供历史数据，它就能自动做出预测。
灵活性强：它能处理各种类型的时间序列数据，不管是每天、每小时甚至每分钟的数据。
可解释性好：Prophet 生成的模型容易理解，你可以清楚地看到它是怎么分析数据的，以及哪些因素影响了预测。

总的来说，Prophet 就是个帮你根据过去的数据信息，自动预测未来变化趋势的小工具，操作起来不复杂，非常适合初学者用来做时间序列预测的入门工具。

理论基础

Prophet 是一种基于加性模型，能够分解时间序列为多个不同的部分：趋势（Trend）、季节性（Seasonality） 和假期效应（Holidays effects）。

在详细讲解 Prophet 的数学原理之前，咱们需要理解它的基本结构~

Prophet 模型公式可以表示为：

其中：

是时间时刻的观测值（即实际的时间序列数据）。
是时间时刻的趋势函数，描述数据的长期趋势。
是时间时刻的季节性函数，捕捉周期性的波动。
是时间时刻的假期效应，用于建模特殊事件或假期对数据的影响。
是噪声项或误差项，通常假设其服从正态分布。

接下来，咱们详细介绍 Prophet 各个部分的数学原理。

1. 趋势（Trend）模型：

Prophet 提供了两种趋势模型：线性趋势和logistic（逻辑）增长趋势。

线性趋势

线性趋势用于建模随时间呈现线性变化的情况。它的数学公式为：

其中：

是线性增长速率。
是变化点（change points）在特定时间点发生速率变化的调整项。
是截距（y 轴上的初始值）。
是截距变化的调整项。

Prophet 会在历史数据中自动识别变化点，即趋势突然发生变化的时间点。在这些变化点，模型中的斜率会进行调整，以适应新的增长趋势。

Logistic 增长趋势

Logistic 增长趋势用于建模增长有上限的情况（如市场饱和）。logistic 增长趋势的公式为：

其中：

是增长的上限（即饱和值）。
是增长速率。
是曲线的中心点，即曲线增长最快时的时间点。

Logistic 模型特别适合那些增长一开始很快，但最终趋向于稳定或饱和的数据场景，比如市场中的产品销售，随着时间推移，增长会逐渐减慢。

2. 季节性（Seasonality）模型：

季节性函数负责捕捉周期性波动，比如销售额的周末效应或每年的季节性波动。Prophet 使用傅里叶级数来近似表达季节性变化：

其中：

是季节性的周期长度（例如一年为 365.25 天，或者一周为 7 天）。
和是傅里叶系数，反映了每个正弦波分量的权重。
是傅里叶级数的阶数，决定了模型的复杂度。较大的可以捕捉更复杂的周期模式。

傅里叶级数的优势在于可以有效表达任何周期性波动，不管波动是简单的正弦曲线还是更复杂的周期性变化。

3. 假期效应（Holiday Effects）：

假期效应模型用来处理特定日期或时间段对时间序列的短期影响。它使用一个指示函数来表示某些假期或特殊事件：

其中：

表示第个假期的时间段。
是一个指示函数，当在假期期间时，取值为 1，否则为 0。
表示假期对数据的影响程度。

Prophet 不仅可以处理假期当天的影响，还可以处理假期前后的效应（如假期前的购物高峰和假期后的疲软期）。用户可以手动指定假期和相关日期，模型会根据数据自适应地学习这些效应的强度。

4. 误差项（Residual/Error）：

是误差项，表示模型和实际数据之间的差异。通常假设误差服从正态分布，即，其中是标准差。

Prophet 在拟合模型时，使用最大似然估计（Maximum Likelihood Estimation，MLE）方法来找到最优参数，最小化模型的误差。

5. 模型拟合与优化

Prophet 的核心目标是通过对趋势、季节性和假期效应的加性分解来拟合时间序列数据。为了优化模型，Prophet 使用了斯坦（Stan）库，斯坦是一个用于贝叶斯推理的概率编程语言。具体来说，Prophet 使用了广义的极大似然估计（Generalized Maximum Likelihood Estimation）和马尔科夫链蒙特卡洛（MCMC）方法来估计模型参数。

Prophet 首先将所有的趋势、季节性和假期效应参数转化为一个优化问题，接着通过斯坦模型优化这些参数。拟合过程中，它会根据历史数据自适应地选择变化点和季节性周期，尽可能准确地捕捉数据中的变化模式。

6. 预测过程

拟合好模型之后，Prophet 用这个模型来进行未来的预测。预测的步骤是：

对未来的时间点使用拟合好的（趋势），估计它的趋势值。
使用来计算未来时间点的季节性波动。
如果未来时间点有假期效应，则考虑的影响。
最终的预测值为这几个部分的加总，即，再加上噪声。

总结 Prophet 算法流程

输入数据：输入一段时间序列数据以及对应的时间戳。
趋势建模：

如果是线性趋势，则通过拟合的形式来拟合数据。
如果是 Logistic 增长趋势，则通过拟合来模拟饱和增长。

季节性建模：使用傅里叶级数建模，并找到周期性波动模式。

假期建模：根据提供的假期列表，调整模型，加入假期效应。

误差处理：拟合过程中考虑误差项，通常假设为正态分布。

参数优化：使用斯坦模型来优化参数，最小化误差。

预测未来：基于拟合的趋势、季节性和假期效应，预测未来的时间序列值。

Prophet 通过这种加性分解方法，可以非常灵活地处理各种复杂的时间序列数据。

一个完整案例

下面给大家展示使用 Prophet 进行时间序列预测，结合实际数据进行数据分析~

假设咱们是一家零售公司，希望预测未来一年的销售额趋势，并且想要考虑季节性、假期效应以及趋势变化点等因素。咱们将使用 Prophet 来预测和分析销售额数据。

Step 1: 数据准备

咱们将从一个包含历史销售额数据的数据集中开始。

该数据集包含以下列：

日期（date）：销售日期
销售额（sales）：该日期的实际销售额
假期信息（可选）：特殊日期，如圣诞节、黑色星期五等

在这个例子中，咱们假设已经有了这类数据并将其导入 Python 环境。

import pandas as pd
import numpy as np
from prophet import Prophet
import matplotlib.pyplot as plt

# 创建示例销售数据集，假设是从2018年到2023年的每日销售额
date_range = pd.date_range(start='2018-01-01', end='2024-12-31')
np.random.seed(42)
sales = 500 + 5 * np.sin(2 * np.pi * date_range.dayofyear / 365.25) + np.random.normal(0, 30, len(date_range))

# 创建一个 DataFrame 存储数据
data = pd.DataFrame({
    'date': date_range,
    'sales': sales
})

# 将列名转换为 Prophet 要求的 'ds' 和 'y'
data.rename(columns={'date': 'ds', 'sales': 'y'}, inplace=True)

# 可视化数据
plt.figure(figsize=(10, 6))
plt.plot(data['ds'], data['y'], label='Daily Sales')
plt.title('Historical Daily Sales')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.legend()
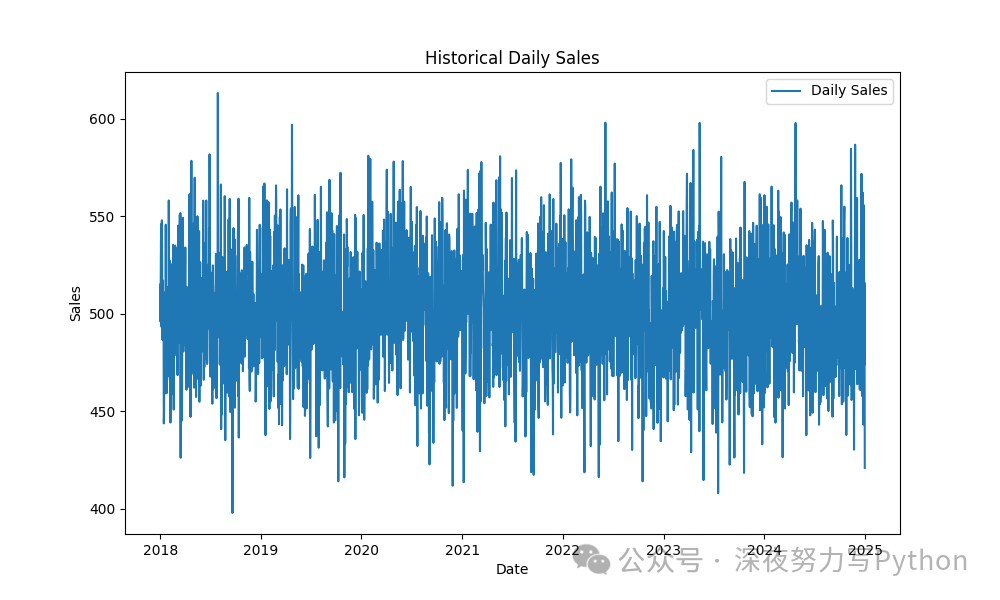
plt.show()

在这一步中，咱们生成了一个销售额随时间变化的图表，显示了每天的销售趋势。

Step 2: 使用 Prophet 进行初步建模

接下来，咱们使用 Prophet 模型来对销售额进行预测。首先，咱们定义模型并拟合数据，然后对未来一年（2024年）的销售额进行预测。

# 初始化 Prophet 模型
model = Prophet(yearly_seasonality=True, weekly_seasonality=True, daily_seasonality=False)

# 拟合模型
model.fit(data)

# 预测未来一年（2024年）
future = model.make_future_dataframe(periods=365)
forecast = model.predict(future)

# 可视化预测结果
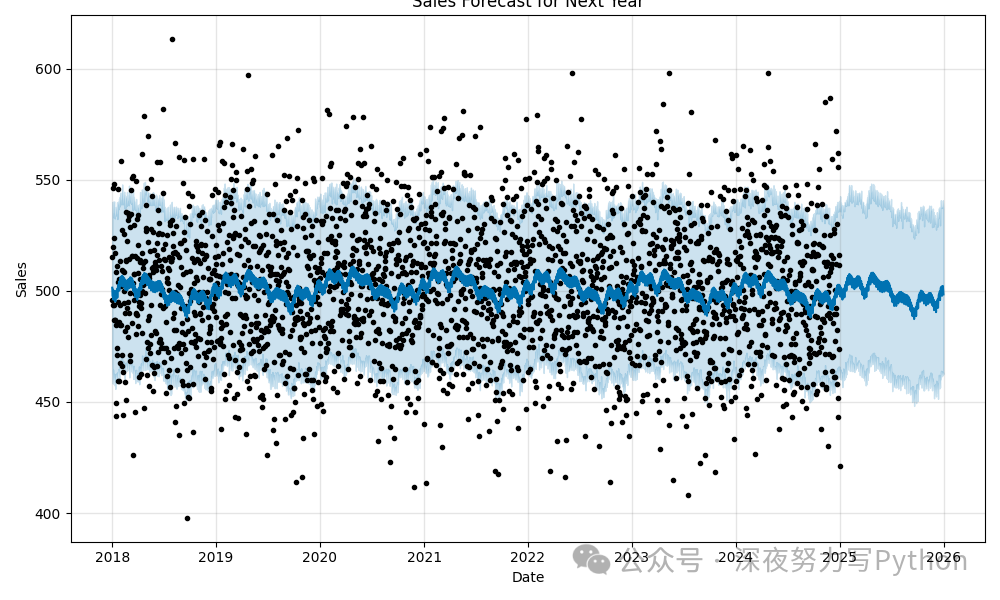
fig1 = model.plot(forecast)
plt.title('Sales Forecast for Next Year')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.show()

这张图展示了 Prophet 模型的初步预测结果，包括历史数据和未来一年的销售预测。

Step 3: 模型成分分解分析

为了进一步分析 Prophet 模型的预测，咱们可以分解出趋势、季节性和假期效应的影响。

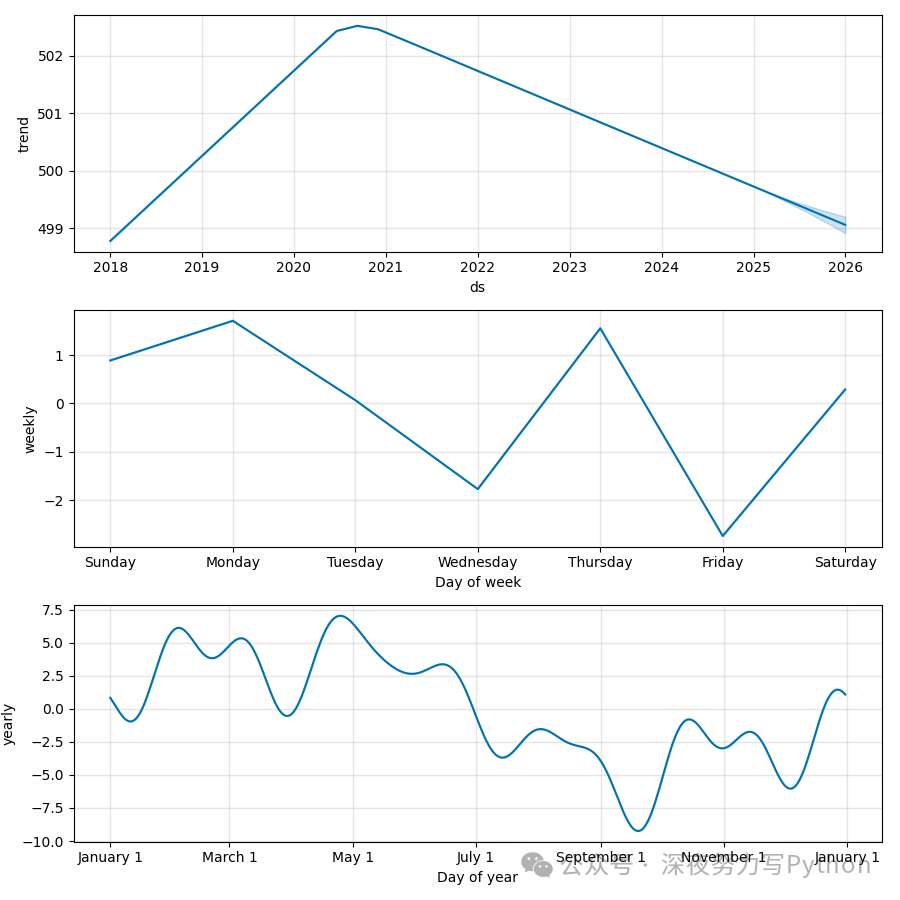
# 分解成分
fig2 = model.plot_components(forecast)
plt.show()

这张图展示了 Prophet 模型的不同组成部分，包括长期趋势、年度季节性以及周内模式。

趋势图：展示了时间序列的长期增长或衰退趋势。
年度季节性：展示了一年中的季节性变化，比如夏季、冬季的销售高峰。
周内季节性：展示了一周中的销售波动，例如周末销售较高。

Step 4: 假期效应

假设咱们要引入假期效应，例如黑色星期五和圣诞节对销售额的影响。咱们可以通过 Prophet 的 add_country_holidays 方法加入这些影响因素。

# 初始化 Prophet 模型，添加假期效应
model_with_holidays = Prophet(yearly_seasonality=True, weekly_seasonality=True)
model_with_holidays.add_country_holidays(country_name='US')

# 拟合模型
model_with_holidays.fit(data)

# 预测未来一年（包含假期效应）
future_with_holidays = model_with_holidays.make_future_dataframe(periods=365)
forecast_with_holidays = model_with_holidays.predict(future_with_holidays)

# 可视化预测结果（包含假期效应）
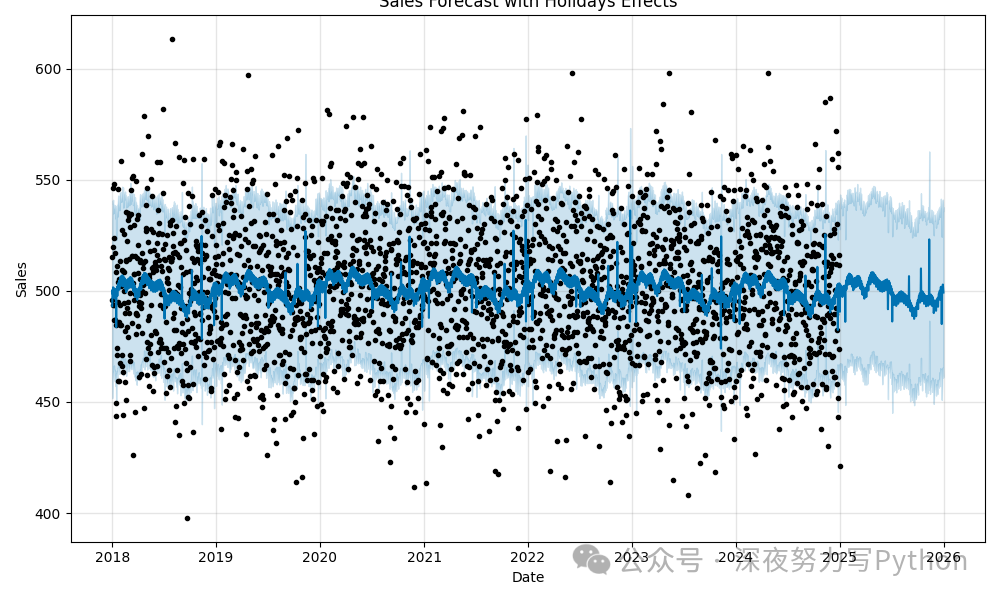
fig3 = model_with_holidays.plot(forecast_with_holidays)
plt.title('Sales Forecast with Holidays Effects')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.show()

这张图展示了包含假期效应的销售预测，假期效应可能导致销售额在特定日期急剧增长或下降，例如圣诞节期间的销售激增。

Step 5: 模型优化

为了提升 Prophet 模型的预测性能，咱们可以调整模型的一些关键参数：

变化点（Change Points）：调整趋势的变化点，增加模型对长期趋势变化的敏感性。
正则化参数：通过调整趋势和季节性正则化参数，避免过拟合。

调整变化点和正则化参数：

# 设置较高的变化点正则化强度，避免趋势过拟合
model_optimized = Prophet(
    changepoint_prior_scale=0.05,  # 较低的变化点正则化参数
    seasonality_prior_scale=10,    # 较高的季节性正则化参数
    yearly_seasonality=True, 
    weekly_seasonality=True
)

# 拟合优化后的模型
model_optimized.fit(data)

# 预测未来一年
future_optimized = model_optimized.make_future_dataframe(periods=365)
forecast_optimized = model_optimized.predict(future_optimized)

# 可视化优化后的预测结果
fig4 = model_optimized.plot(forecast_optimized)
plt.title('Optimized Sales Forecast')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.show()

这张图展示了通过调整 Prophet 模型参数后，更加平滑和合理的销售预测结果。

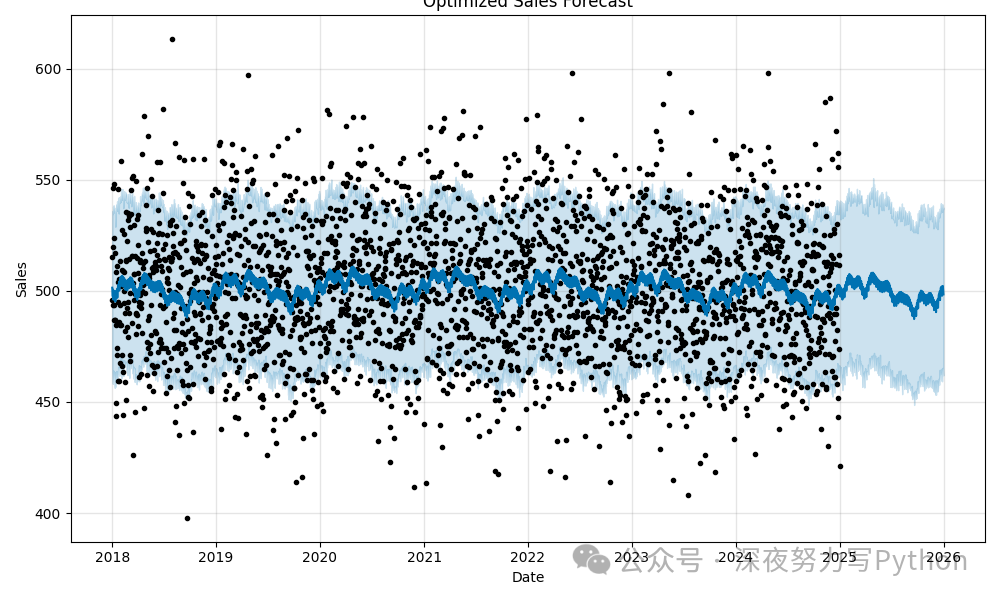
趋势解读：通过 Prophet 模型的分解，咱们可以看到销售额的长期趋势。例如，销售额可能在某个时间段呈现线性增长，但由于假期或其他外部因素出现变化点，这时销售额可能有大幅波动。
季节性效应：年度季节性表明，销售额在特定季节波动较大，例如假期期间销售额上涨，冬季销售量可能降低。
假期效应：加入假期效应后，模型能够更加准确地捕捉到某些特殊时间段的销售波动，这对零售行业尤其重要。
模型优化：通过调整变化点和正则化参数，咱们避免了过拟合，得到了更稳定和更合理的预测结果。

模型分析

优点

简单易用：

易上手：Prophet 是一个面向非专家的数据科学工具，使用简单，特别适合时间序列预测的新手用户。它不需要用户进行复杂的特征工程，甚至对于趋势、季节性等因素，Prophet 都能自动检测和拟合。
自动处理节假日和季节性变化：Prophet 内置对节假日、季节性、周末等因素的处理，可以自动调整模型，尤其在零售、旅游等有明显季节性波动的行业中很有用。

灵活性高：

趋势变化检测：Prophet 自动检测趋势的变化点（change points），并能有效捕捉数据中存在的突然增长或衰退趋势。例如，在市场竞争变化时，销售额增长的速度可能突然发生改变，Prophet 可以对此进行自适应调整。
长短期预测：Prophet 可以适用于从日级别到年级别的时间序列数据，无论数据频率是高是低，适应性强。

处理缺失数据的鲁棒性：

缺失值和异常值的耐受性：相比其他时间序列算法，Prophet 对缺失值和异常值的敏感度较低，能够自动处理并拟合带有噪声的数据。

可解释性：

可分解性：Prophet 将时间序列分解为趋势、季节性、假期效应等部分，这样的分解方式具有较好的可解释性，方便理解模型的预测机制和每个成分对预测的贡献。

缺点

无法处理高频数据：

高频时间序列的适应性较差：对于超高频（如每秒或每分钟的金融数据等），Prophet 的性能会下降，因为它设计主要用于日常、每周、每月或季度的时间序列。面对这些高频数据，Prophet 的加性模型和趋势变化检测能力有限。

对非线性趋势建模的局限性：

对复杂非线性模式适应性较弱：尽管 Prophet 支持线性和 Logistic 趋势建模，但面对更复杂的非线性变化（如明显的平稳期、振荡、反复周期等），它的能力相对不足。相较于深度学习模型如 LSTM，Prophet 在复杂数据模式捕捉上存在劣势。

没有交互效应：

无法捕捉复杂交互特征：Prophet 主要基于时间来建模时间序列，无法处理交互特征（如多维时间序列的关联关系）。例如，销售额可能与价格、广告投放量等外部因素有关，Prophet 没有原生的支持来捕捉这种交互关系。

假设趋势线性：

趋势建模简单：Prophet 假设趋势的增长是线性或 Logistic 的，面对更复杂或非线性的长期趋势（如波动、快速衰退等），其表现不够理想，可能会导致欠拟合。

与其他时间序列模型的对比

与 ARIMA 模型对比：
适用场景对比：

Prophet 更适合数据存在明显的季节性、假期效应且趋势多变的场景，操作简单，适合非专业用户。
ARIMA 更适合具有强自相关性的时间序列，尤其适用于线性增长或差分平稳的数据集，但需要较高的建模技巧和对数据进行预处理。
ARIMA（自回归积分滑动平均模型）是一种经典的时间序列模型，它假设时间序列由自回归（AR）、差分（I）和移动平均（MA）部分组成。
优点：ARIMA 对趋势和季节性的假设较为明确，适用于线性增长或平稳的时间序列。ARIMA 在捕捉自相关性上表现良好，能够处理序列中的滞后效应。
缺点：ARIMA 需要对数据进行差分处理，以使时间序列平稳，操作相对复杂。对于数据中存在的多重季节性和变化点，ARIMA 表现不佳，且缺乏自动化的假期效应处理能力。

与 LSTM（长短期记忆网络）对比：

适用场景对比：

Prophet 适合中小型数据集的时间序列预测，并且要求结果具有可解释性和模型灵活性，尤其在数据较为稀疏、缺失的情况下仍能有较好的表现。
LSTM 适合大规模复杂的非线性时间序列预测，特别是在金融、能源等对预测准确性要求高且时间序列具有复杂模式的领域表现优越。
LSTM 是一种基于 RNN（循环神经网络）的深度学习算法，特别擅长捕捉长序列中的依赖关系，能够记住较长时间跨度的模式。
优点：LSTM 在处理复杂的非线性时间序列方面表现优异，能够适应长序列中的模式、交互关系等。可以自动学习数据中的滞后和趋势效应，而无需手动处理。
缺点：LSTM 对数据量需求较大，需要大量的数据进行训练，才能发挥深度学习的优势。模型训练耗时长、计算资源需求高，且不具备像 Prophet 那样的高可解释性。

与 XGBoost 对比：