利用数值方法求解偏微分方程partial differential equations (PDEs) 是工程和医学中普遍存在的任务。然而,当评估多个几何图形上的偏微分方程PDE解决方案时,计算成本可能高得惊人。今日,美国 约翰斯·霍普金斯大学(Johns Hopkins University)Minglang Yin,Natalia Trayanova & Mauro Maggioni等,在Nature Computational Science上发文,旨在通过引入微分同胚映射算子学习Diffeomorphic Mapping Operator Learning (DIMON)来解决这一挑战,DIMON是一种通用的人工智能框架,可以在各种几何上学习不同类型PDE,这取决于几何的解算子。
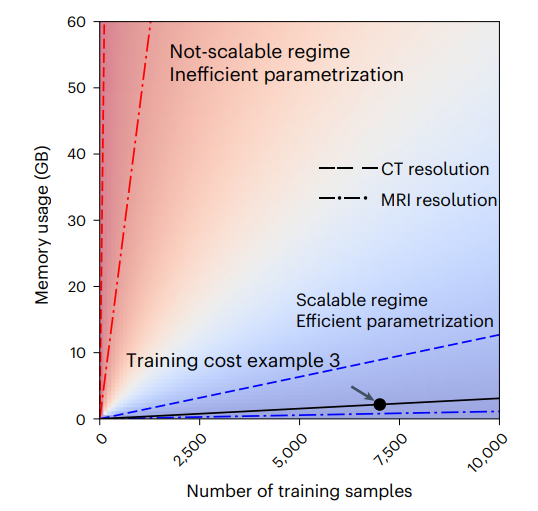
还给出了几个例子,以展示这一框架在参数化和非参数化领域中,学习静态和时间相关偏微分方程的性能、效率和可扩展性。其中包括解拉普拉斯方程、反应扩散方程和多尺度偏微分方程系统,这一系统描述了个性化数字孪生心脏的数千个电传播。DIMON可以用更少的计算资源,将多个几何上的解近似计算成本从数小时减少到数秒。
A scalable framework for learning the geometry-dependent solution operators of partial differential equations.
学习偏微分方程几何相关解算子的可扩展框架。
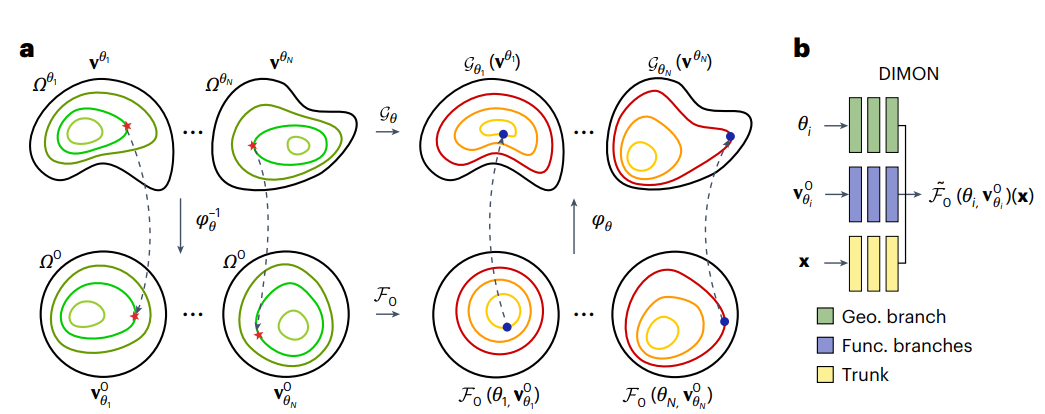
图1: 在DIMON微分同胚域上,学习偏微分方程的几何依赖解算子。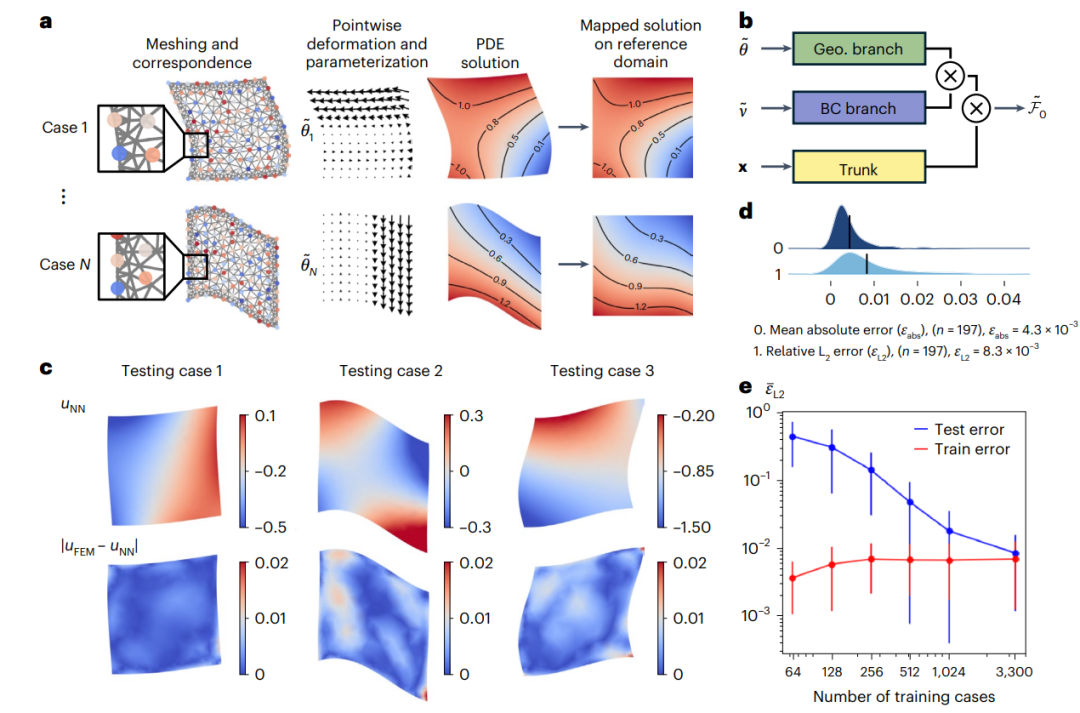
图2:在参数化的二维区域上,学习拉普拉斯方程的解算子DIMON。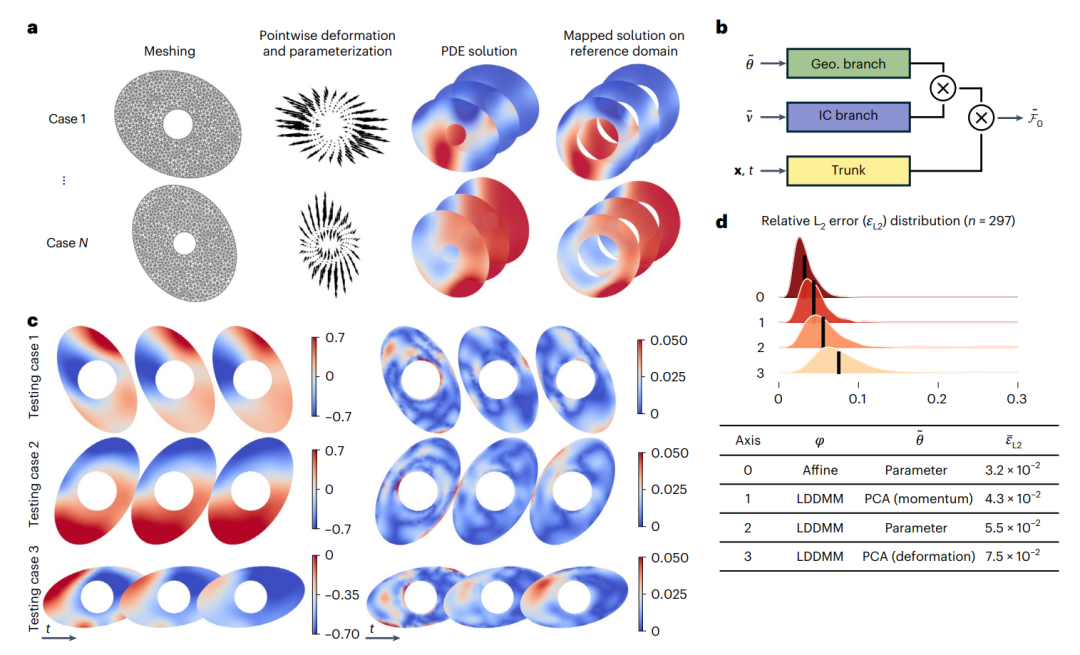
图3: 参数二维区域上,反应扩散方程学习解算子DIMON。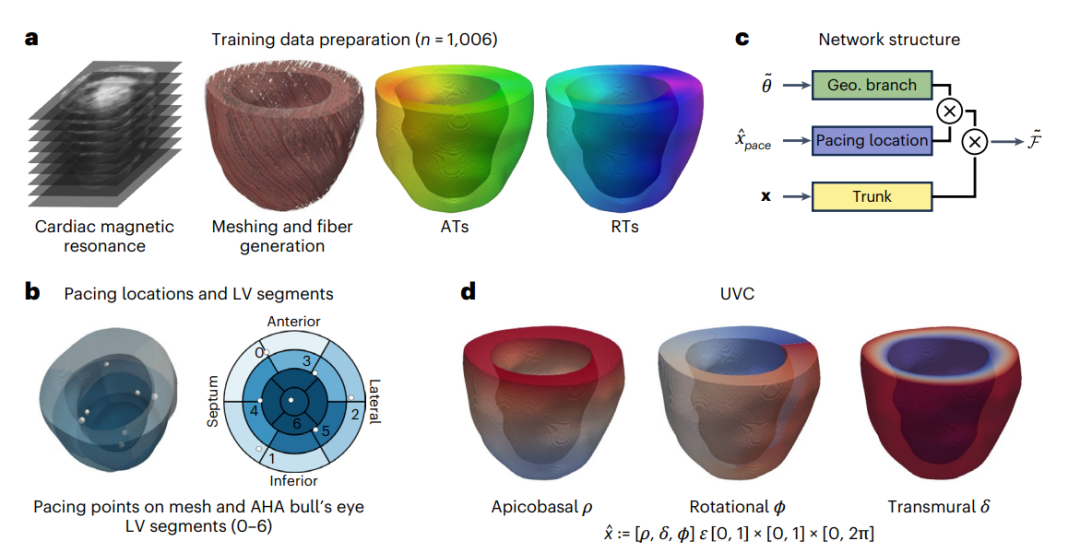
图4: 预测患者特异性左心室left ventricles,LV上的电信号传播。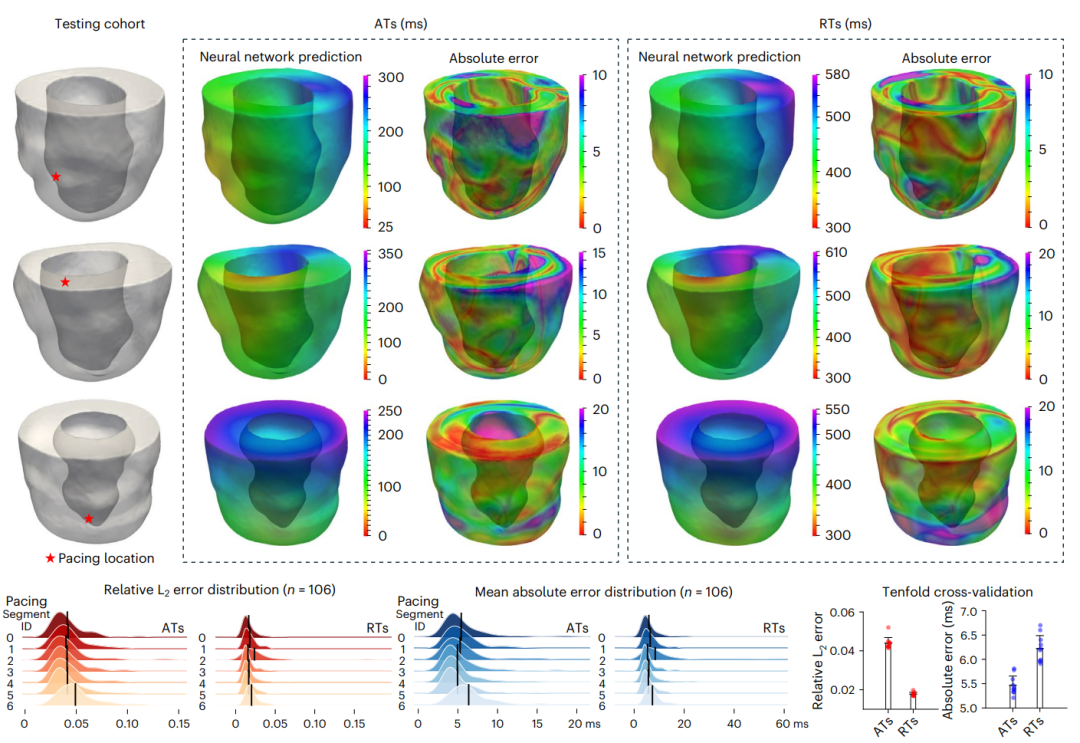
文献链接
Yin, M., Charon, N., Brody, R. et al. A scalable framework for learning the geometry-dependent solution operators of partial differential equations. Nat Comput Sci (2024).
https://doi.org/10.1038/s43588-024-00732-2
https://www.nature.com/articles/s43588-024-00732-2
本文译自Nature。
来源:今日新材料
声明:仅代表译者观点,如有不科学之处,请在下方留言指正!