今天,我们将运用Python来搭建一个简单的神经网络模型!并深入浅出地探索其背后的运作原理。
提及神经网络时,我们可以将其视为一个高度灵活的函数来理解和应用。
为了做出准确的预测,我们需要构建能够同时组合多个输入的神经网络。,神经网络完全具备这种能力。
拥有多个输入意味着我们也将拥有多个权重,
我们的新神经网络将能够在每次预测时同时接受多个输入。
这使得网络能够结合各种形式的信息来做出更明智的决策,但使用权重的基本机制并未改变。
我们仍然会对每个输入进行处理,就像通过各自的“音量旋钮”一样。换句话说,我们将每个输入乘以它自己的权重。
这里的新特性是,由于我们有多个输入,我们需要将它们的各自预测值相加。因此,我们首先将每个输入乘以其对应的权重,然后将所有局部预测值相加。
这被称为输入的加权和,简称加权和。也有人称之为点积,我们稍后会看到这一点。
weights = [0.1, 0.2, 0]
def neural_network(input,weights): pred = w_sum(input,weights) return pred
def w_sum(a,b): assert(len(a) == len(b)) output = 0 for i in range(len(a)): output += (a[i] * b[i]) return output
fingers = [8.5, 9.5, 9.0]wlrec = [0.65, 0.8,0.8,0.9]nfans = [1.2, 1.3, 0.5, 1.0]
input = [fingers[0], wlrec[0], nfans[0]]
prediction = neural_network(input,weights)
print(prediction)

我们使用Jupyter笔记本运行这个示例,旨在将启动成本降到最低。
Jupyter Notebook地址:
https://jupyter.org/try-jupyter/notebooks/?path=notebooks/Intro.ipynb
一个由WASM驱动的、在浏览器中运行的Jupyter。
接下来我们需要了解背后一个非常重要的逻辑概念——点积(Dot Product)。
我还为大家整理了一些我自己学习深度学习、神经网络用的的学习资料大家添加小助手既可获取,
记得发送文章标题截图给小助手哦!

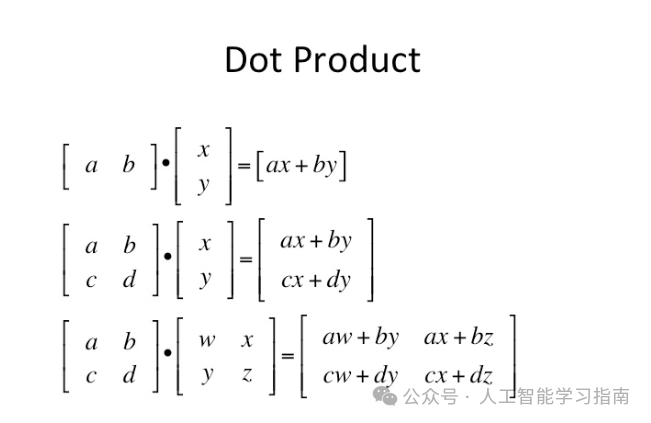
理解点积(加权和)的工作原理及其背后的原因,是真正掌握神经网络如何进行预测的关键部分之一。
简而言之,点积能给我们两个向量之间相似性的概念。这在GPT等模型中尤为重要。比如这些例子:
代码
两个完全相同的向量之间的加权和(w_sum(c,c))最大。
相反,因为a和b没有重叠的权重,所以它们的点积为零。
最有趣的加权和可能是c和e之间的,因为e有一个负权重,这个负权重抵消了它们之间的正相似性。
但是,e与自身的点积会产生数字2,尽管e有负权重(双负变正)。
让我们来熟悉一下点积操作的各种性质。
点积的一些快速数学性质
有时,你可以将点积的性质等同于逻辑与(AND)操作。考虑a和b:
a = [ 0, 1, 0, 1] b = [ 1, 0, 1, 0]
b = [ 1, 0, 1, 0] c = [ 0, 1, 1, 0]
b和c之间有一个列共享了相同的值。这通过了逻辑与(AND)测试,因为b[2]和c[2]都有权重。
正是这一列(且仅这一列)使得分数上升至1。
c = [ 0, 1, 1, 0] d = [.5, 0,.5, 0]
幸运的是,神经网络也能够模拟部分逻辑与(AND)操作,虽然这种表述不太准确。
在这个例子中,c和d与b和c共享同一列,但由于d在该列的权重只有0.5,所以最终得分仅为0.5。
在神经网络中建模概率时,我们会利用这一性质。
d = [.5, 0,.5, 0] e = [-1, 1, 0, 0]
在这个类比中,负权重往往意味着逻辑非(NOT)操作,因为任何正权重与负权重配对都会导致分数下降。
此外,如果两个向量都有负权重(如w_sum(e,e)),则神经网络会执行双非(double NOT)操作,反而增加权重。
另外,你也可以说这是在逻辑与之后的逻辑或(OR),因为如果任何一行显示权重,分数就会受到影响。
因此,对于w_sum(a,b),如果(a[0] AND b[0]) OR (a[1] AND b[1])等成立,那么w_sum(a,b)将返回一个正分数。如果有一个值是负的,那么那一列就相当于执行了逻辑非。
这为我们提供了一种粗略地解读权重的方法。
这些例子假设你正在执行w_sum(input,weights),而这些if语句的“那么”部分是抽象的“那么给予高分”。
weights = [ 1, 0, 1] => if input[0] OR input[2] weights = [ 0, 0, 1] => if input[2]
weights = [ 1, 0, -1] => if input[0] OR NOT input[2] weights = [ -1, 0, -1] => if NOT input[0] OR NOT input[2] weights = [ 0.5, 0, 1] => if BIG input[0] or input[2]
注意在最后一行中,weight[0] = 0.5意味着对应的input[0]必须更大才能补偿较小的权重。
非常重要的一点是,这些只是权重!

权重是“连接”神经元的线。
预测本身不过是调整权重以匹配某个函数。
我们将深入探讨函数匹配的实际含义,神经网络做出预测时意味着什么呢?
weights = [0.1, 0.2, 0]
input = [fingers[0], wlrec[0], nfans[0]]
prediction = neural_network(input,weights)
粗略地说,它意味着网络根据输入与权重的相似度给输入打出高分。
请注意,在以下示例中,nfans在预测中被完全忽略,因为与之关联的权重为0。
最敏感的预测因子是wlrec,因为它的权重为0.2,但高分的主要因素是脚趾数量(ntoes),不是因为它的权重最高,而是因为输入与权重的组合值远高于其他。
另外还有几个需要注意点:
你不能随意打乱权重的顺序,因为它们需要处于特定的位置。
此外,权重值和输入值共同决定了对最终得分的整体影响。
最后,负权重会导致某些输入降低最终预测值(反之亦然)。
大家觉得这篇文章有帮助的话记得分享给你的朋友、同学、闺蜜、敌蜜、死党!