标量
标量是一个单一的数字,例如:24、5、-1或3等。
在线性代数中,标量经常出现在涉及矩阵和向量的运算中。我们用“标量-矩阵乘法”来指代“用一个数与矩阵相乘”的操作,该操作通过标量缩放矩阵或向量,其结果取决于具体上下文——可能是另一个矩阵或变换后的向量。
现在看起来可能有点抽象,但随着你深入学习,一切都会变得更加清晰。我只是在这里先介绍一下。
向量
向量是一个数学实体,既有大小(多少)又有方向(去哪里)。
但还有一种看待向量的方式:它是一个有序的数字列表,告诉你如何在不同方向上移动。
为什么是有序列表?因为向量中数字的顺序很重要,改变顺序会改变向量本身。
在数学上,二维、三维和n维空间中的向量v可以表示为:

第一个数字告诉你水平方向上移动的距离,第二个数字则告诉你垂直方向上移动的距离。
如果我们再加上第三个数字,那将表示在深度方向上移动的距离,从而为空间增加了一个新的维度。
类似地,在n维空间中,每一个额外的数字都会告诉你在该对应维度上移动的距离。
例如:
在二维空间中,向量v由两个分量[3, 4]组成,这实际上是在指导你沿x轴方向移动3个单位,沿y轴方向移动4个单位。
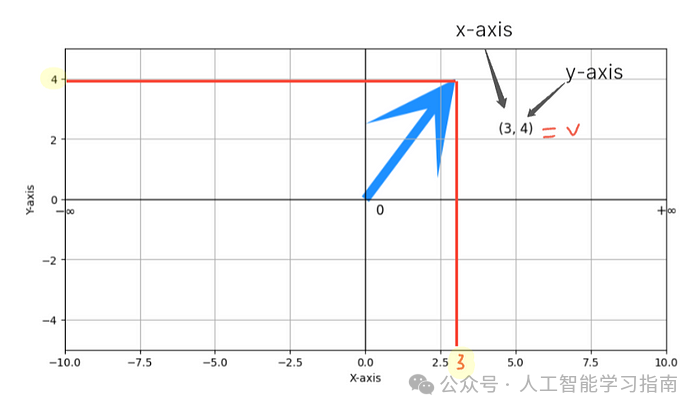
向量的模
箭头(向量)的长度被称为其模。模的大小可以通过勾股定理来计算。
以我们的例子为例,模的大小为
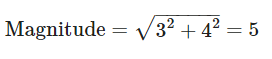
这意味着从原点出发,向量总共移动了5个单位的距离。
为什么向量在深度学习中如此重要?
当你将数据输入到深度学习模型中时,这些数据通常会被转换成向量,以便模型进行处理。
例如:
文本处理:句子中的单词可以使用词嵌入等技术表示为向量。
图像处理:图像可以通过将像素值展平成长列表来表示为向量。
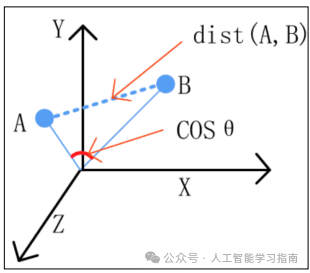
点积与投影
在线性代数中,点积与投影是两个基本概念,它们虽然各自独立,但紧密相连,并在深度学习中扮演着至关重要的角色。
点积是一种数学运算,它接受两个向量并返回一个单一的数,或称标量,给定两个向量a和b,它们的点积a·b计算如下:
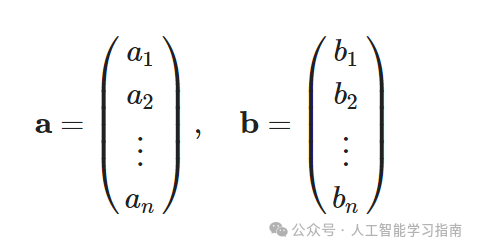
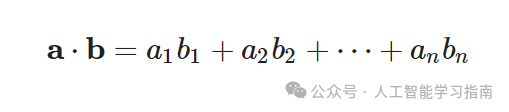
逐分量(代数)形式
从几何角度看,点积可以解释为衡量一个向量与另一个向量的对齐程度。

几何形式
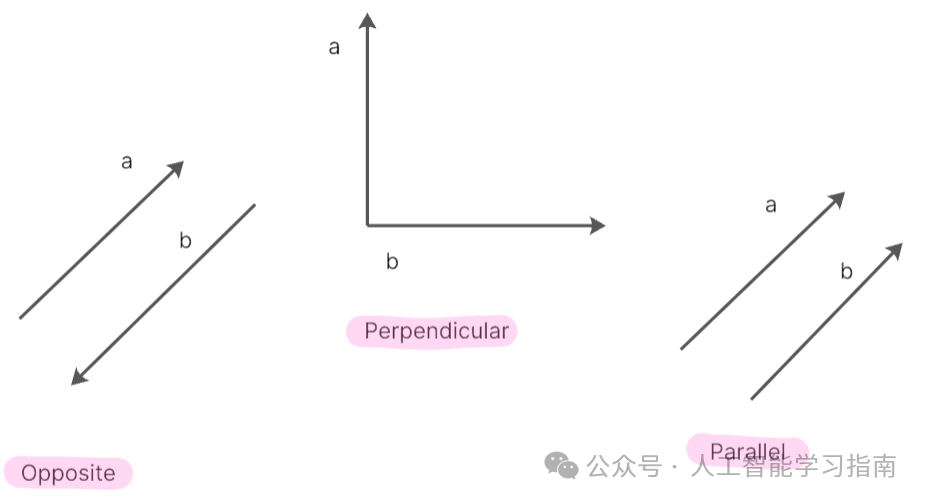
当两个向量同向时,它们的点积为正且较大,因为两向量之间的角度为零,使得cos(0)=1,这表示向量间有很强的对齐性。
如果向量垂直,它们的点积为零,因为两向量之间的角度为90度,cos(90)=0,这表示向量间没有对齐。
当向量反向时,它们的点积为负,因为两向量之间的角度为180度,cos(180°)=-1,这个负值反映了向量在相反方向上对齐,即表示不一致。
点积是神经网络处理信息的核心,每个神经元都会计算其输入向量(如图像的像素值)与权重向量(学习到的参数)之间的点积。
这一操作有助于确定输入与已学习模式之间的对齐程度,从而指导网络的决策过程。
投影
投影建立在点积概念之上,将抽象的对齐度量转化为具体的向量。
向量a在向量b上的投影表示a中沿b方向的分量。
简而言之,点积告诉我们“两个向量在多大程度上一致”,而投影则展示了“一个向量的哪部分与另一个向量对齐”。
投影的计算公式为:
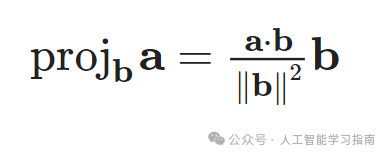
这里,点积a·b的结果向量显示了向量a在向量b方向上的“投影”长度。
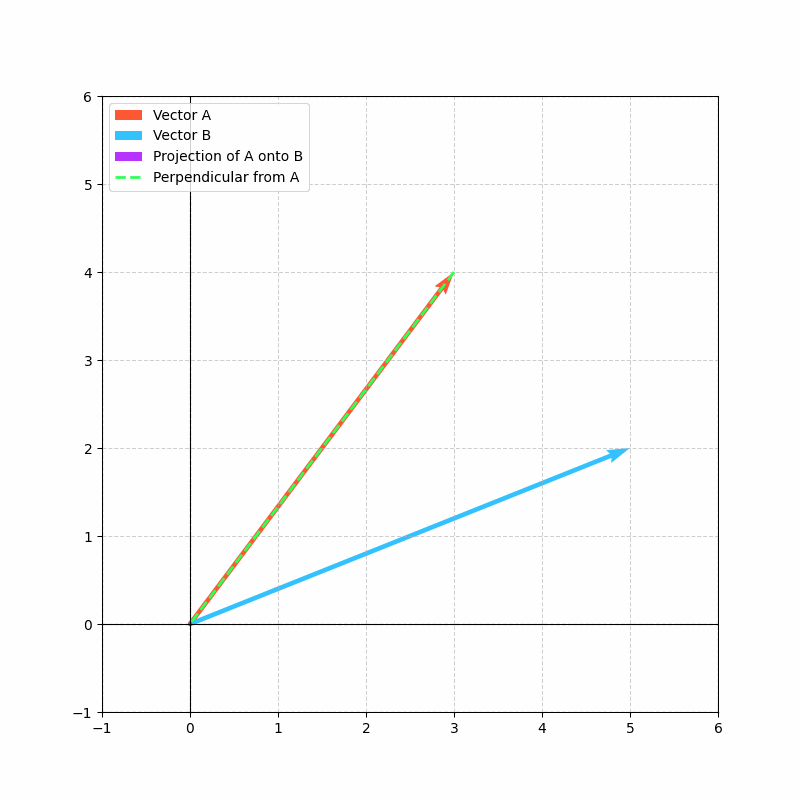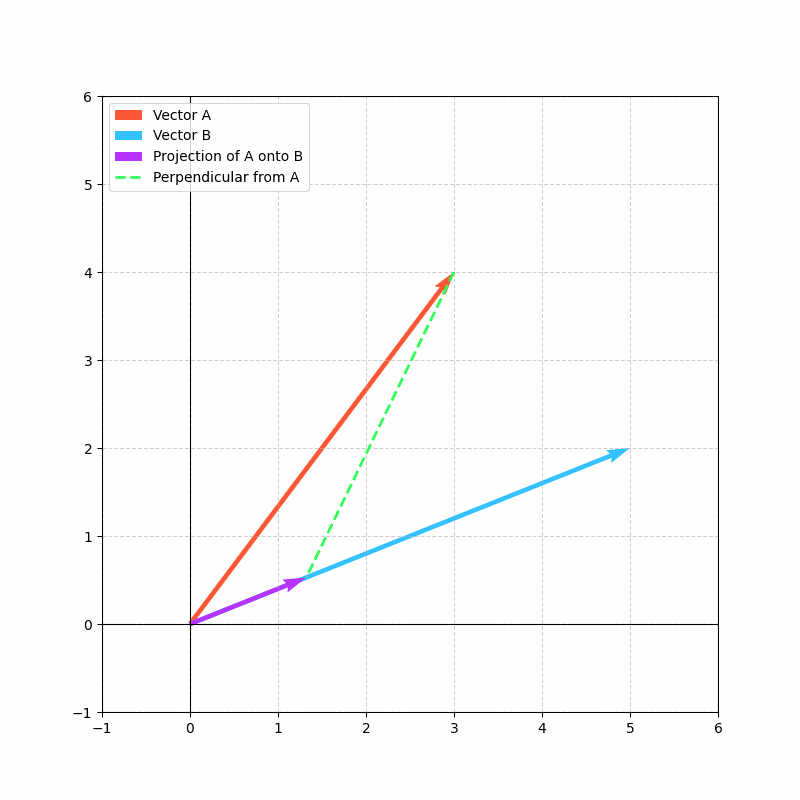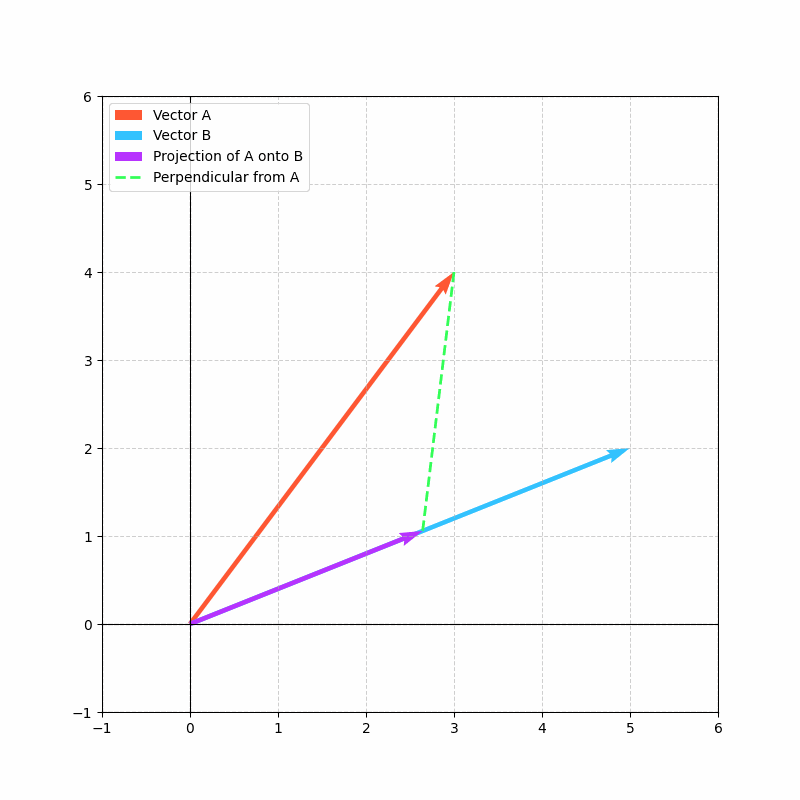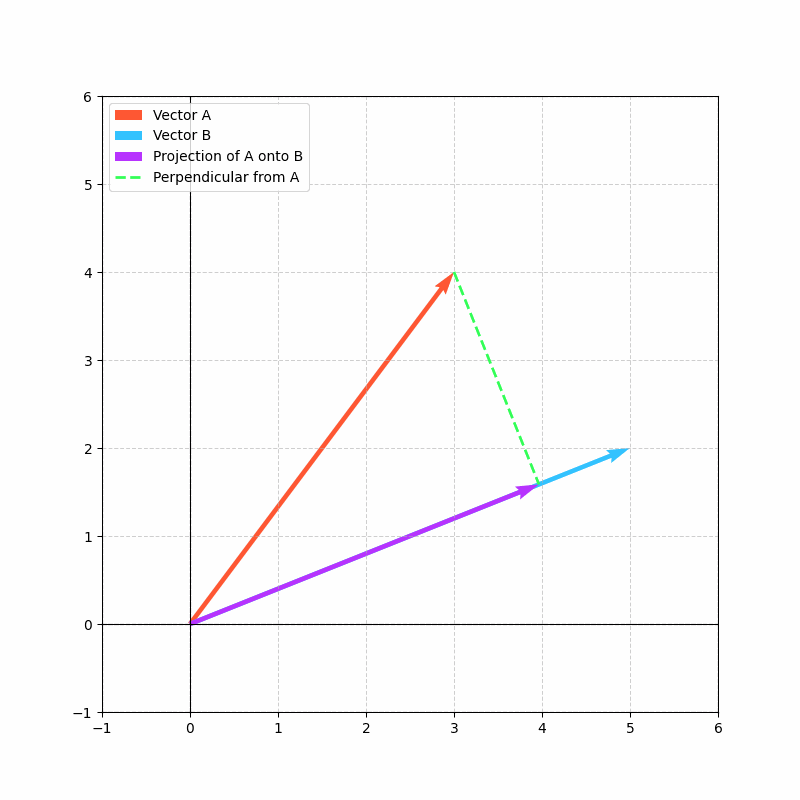
投影对于理解数据在网络层间移动时如何变换至关重要,随着数据被投影到不同方向(学习到的特征),网络能够提取并关注输入数据中最相关的方面。
矩阵与矩阵运算
矩阵是一个由行和列排列的数字矩形阵列,可以视为向量的集合。
注意:“matrices”是“matrix”的复数形式。
矩阵看起来像这样:
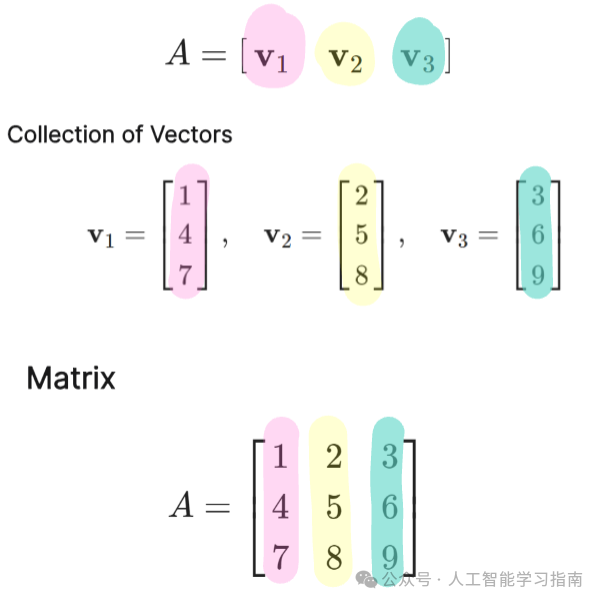
这里,矩阵A有3行3列,因此它是一个3x3矩阵。
在深度学习的背景下,矩阵是基础,因为它们提供了一种结构化的方式来高效地表示和处理数据。
这种结构化的表示方式使得神经网络能够对大型数据集执行复杂的计算。
矩阵作为平面
基本矩阵运算
基本矩阵运算用于转换数据、组合特征以及执行神经网络训练和运行中的核心计算。
在深度学习中,矩阵的某些常见操作至关重要,如果你掌握了这些操作的工作原理,那么你就为理解深度学习模型的工作方式打下了坚实的基础。
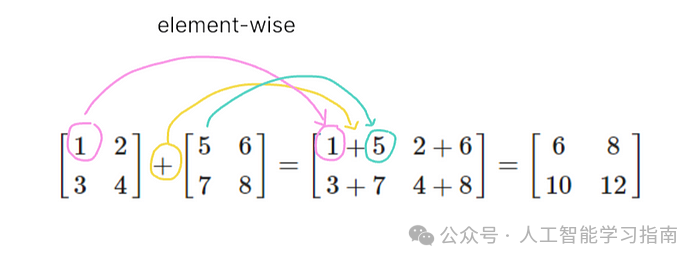
矩阵加法很简单——只有维度相同的两个矩阵才能进行加法运算。
这是因为加法是按元素进行的,即一个矩阵的每个元素与另一个矩阵中对应位置的元素相加。
在神经网络中,矩阵加法常用于合并来自多个神经元或层的输出。
矩阵乘法
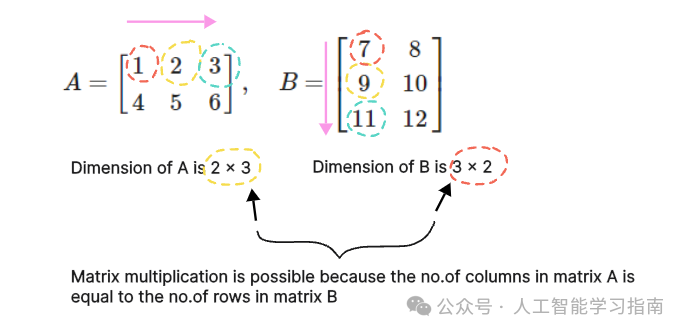
两个矩阵要相乘,必须满足第一个矩阵的列数等于第二个矩阵的行数。
相乘后得到的矩阵的维度由第一个矩阵的行数和第二个矩阵的列数决定。
从数学的角度来说
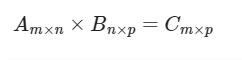
让我们看下它是如何工作的!
你可能会想,如果列数n不等于行数m怎么办呢?
在这种情况下,标准的矩阵乘法是行不通的(未定义)。
如果可能的话,你可以尝试重新调整一个或两个矩阵的形状,使它们的维度适合进行乘法运算,这在需要重新构造或展平数据的场景中很常见。
如果重新调整形状不合适,可以考虑使用按元素乘法(Hadamard积)。
在神经网络中,数据通过各层时会进行变换,每一层的权重矩阵都会与输入矩阵相乘,以产生下一层的输出。
注意:点积是单个神经元内部的基本操作,而当我们同时考虑整个神经元层时,就会用到矩阵乘法。
逐元素乘法
它涉及两个矩阵中对应元素的乘法,这个操作要求两个矩阵具有相同的维度。
例如:假设我们有两个矩阵A和B,它们都是2x3的(2行,3列),但这里只是为了说明,实际上n=m=3(即列数等于行数)。
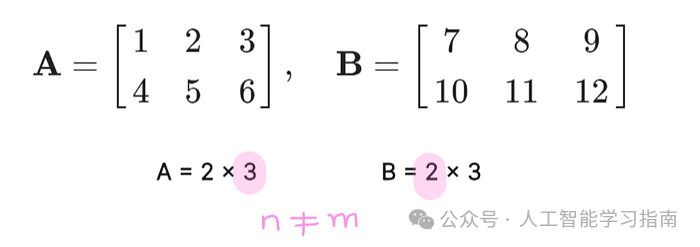
下面是按元素乘法(Hadamard积)的工作方式:
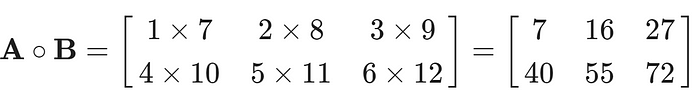
哈达玛积
与矩阵乘法不同,Hadamard积要简单得多,因为它不涉及复杂的行乘列操作,而是直接进行元素对元素的乘法。
这个操作在某些场景下特别有用,比如在神经网络中应用掩码或在卷积层中进行按元素操作。
矩阵转置
矩阵的转置是一种操作,它将矩阵沿其对角线翻转,实际上是将矩阵的行和列互换。
例如:给定一个m x n维的矩阵A,那么A的转置将是一个n x m维的矩阵。
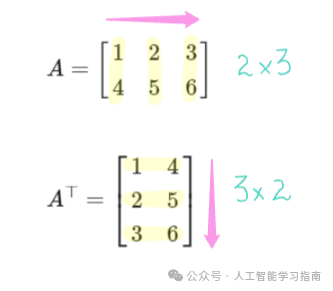
矩阵转置
矩阵转置常用于调整矩阵的维度,特别是在执行如反向传播等操作时,其中梯度的维度必须与神经网络中的权重矩阵正确对齐。
范数与距离度量
范数是一种函数,用于测量向量或矩阵的大小或长度。
对于向量:如果你有一个向量[3, 4],范数将告诉你这个向量的长度。可以想象成从(0, 0)到图上点(3, 4)的线段长度。
对于矩阵:将矩阵视为数字表,矩阵的范数衡量这些数字在表中的“大小”或“分散”程度。
范数类型:
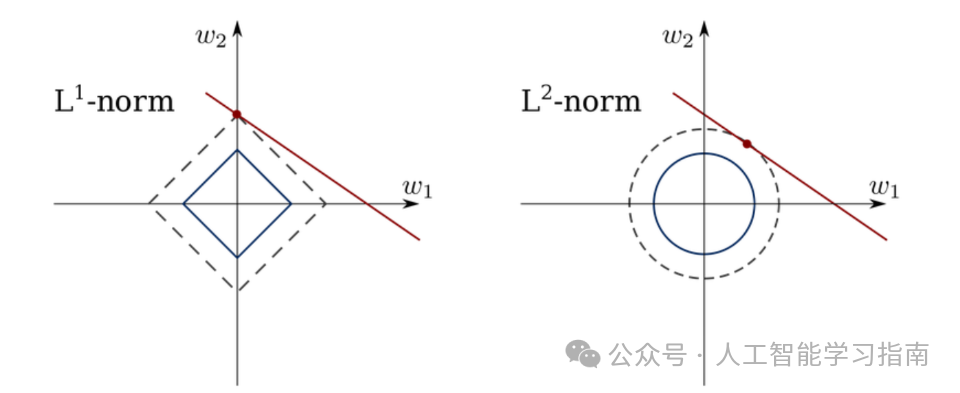
L1范数(曼哈顿范数):绝对值之和(不考虑数的符号的非负值)。它衡量的是“曼哈顿距离”,因此得名。
对于向量v = [1, -2, 3],L1范数计算为:
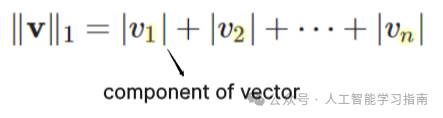
L2范数(欧几里得范数):它是向量各分量平方和的平方根,用于衡量向量与原点的(欧几里得)距离。
这是最常用的范数,在欧几里得空间中常被称为“标准”范数。
对于同一向量v,如果我们计算其L2范数:
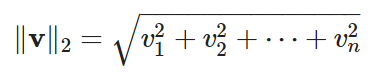
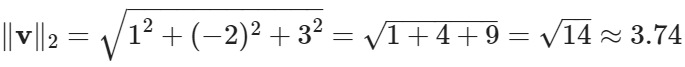
弗罗贝尼乌斯范数:弗罗贝尼乌斯范数是矩阵中所有元素平方和的平方根。
它与L2范数类似,但作用于矩阵的所有元素。
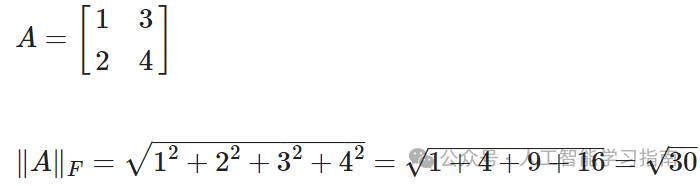
∥A∥F 表示矩阵A的弗罗贝尼乌斯范数。
在深度学习中的应用:
正则化:范数直接应用于正则化技术中,如L1正则化(Lasso)和L2正则化(Ridge)。
在神经网络中,这意味着在损失函数中增加一个项,根据权重的L1和L2范数对其进行惩罚,有助于模型更好地泛化。
优化:在训练过程中,范数有助于控制权重更新的大小。
例如,在梯度下降中,如果梯度较大,范数确保采取的步长不会过大,从而可能破坏训练过程的稳定性。
距离度量
在理解范数之后,重要的是要掌握它们与“距离度量”之间的关系。
距离度量用于衡量两个向量、点或对象之间的分离程度。
范数可用于定义距离度量,这对于测量空间中点(或向量)之间的“分离程度”至关重要。
距离度量的类型:
欧几里得距离:源自L2范数,用于测量空间中两点之间的直线距离。
该度量在许多机器学习算法中都很常见,如K最近邻(KNN)和聚类算法如K均值。
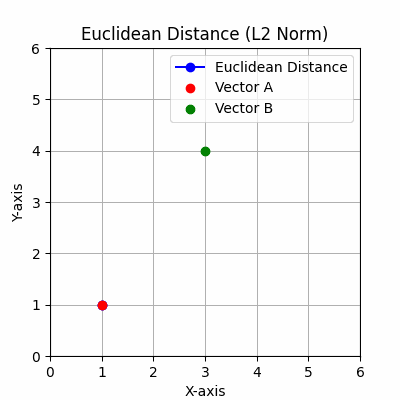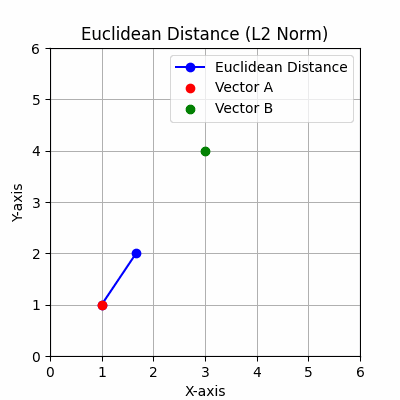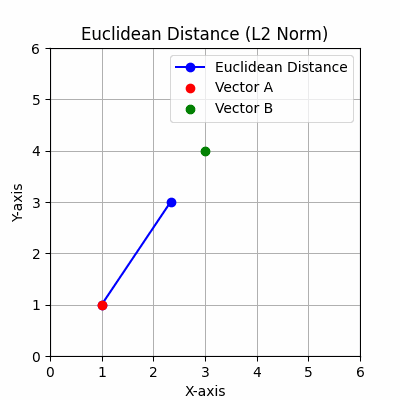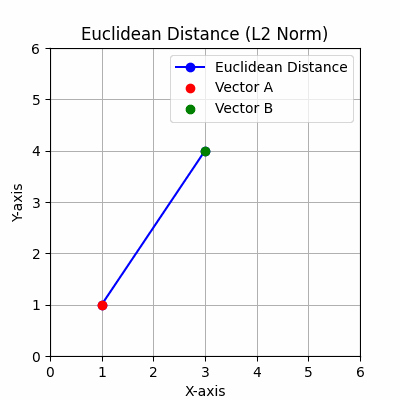
注意:这些是向量A和B的端点。
曼哈顿距离:基于L1范数,它测量两个点在垂直轴上的距离,类似于在网格路径上导航。
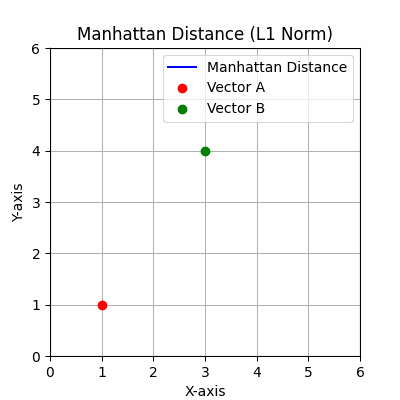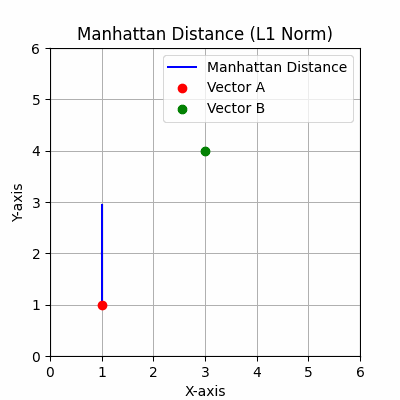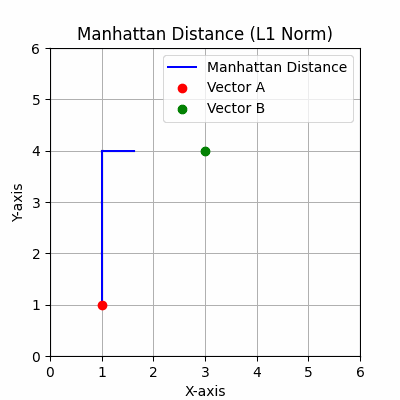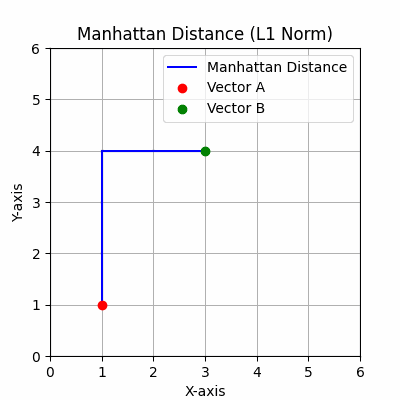
该度量在移动仅限于水平和垂直方向的情况下很有用,如某些优化问题和基于网格的游戏中。
如果大家想更进一步学习机器学习、深度学习、神经网络技术的可以看看以下文章(文章中提到的资料都打包好了,都可以直接添加小助手获取)
大家觉得这篇文章有帮助的话记得分享给你的朋友、同学、闺蜜、敌蜜、死党!