本文在《The 8 Most Important Statistical Ideas of the Past 50 Years》文章的基础上,结合金融量化应用场景,带领大家一起探索过去半个世纪中涌现的一些至关重要的统计学思想,深入浅出地解析这些思想在金融量化领域的应用,并给出相应的Python应用示例。这八大统计学思想,不仅是学术界璀璨的明珠,更是我们解析复杂金融数据集、从中提炼有价值投资见解的得力助手。它们不仅催生了新的统计工具和方法,让金融数据的分析更加精准高效,还见证了这些思想在金融领域的广泛应用,助力投资者做出更加明智的决策。
反事实因果推断(Counterfactual causal inference)是一种从观测数据中做出因果推断的方法。换句话说,它是一种无需随机对照试验即可确定干预或处理变量对结果的影响的方式。这是通过将观察到的结果与未应用干预措施时可能观察到的结果进行比较来实现的。例如,假设我们对一种新药对血压的影响感兴趣。我们可以比较服用了该药物的群体的血压与未服用的类似群体的血压。通过比较这两组,我们可以估计该药物对血压的影响。反事实因果推断已在计量经济学、流行病学和心理学等多个领域得到发展。它使研究人员能够对做出因果推断的条件做出更精确的假设,并促进了解决这些问题的新统计方法的发展。
反事实因果推断在金融量化领域同样具有广泛的应用价值。在金融市场中,经常需要评估某项决策或政策对资产价格、收益率等金融指标的影响。然而,由于金融市场的复杂性和不可预测性,很难进行随机对照试验来直接评估这些影响。因此,反事实因果推断成为了一种重要的工具,它允许我们从观测数据中做出因果推断,而无需进行实际的随机试验。
在金融量化中,反事实因果推断可以通过比较在应用了某种干预(如政策调整、市场变动等)之后观察到的金融指标与未应用该干预时可能观察到的金融指标来实现。例如,假设我们对某项新政策对股票价格的影响感兴趣。我们可以比较政策实施后股票价格的变动与政策未实施时基于历史数据模拟的股票价格变动。通过比较这两组数据,我们可以估计该政策对股票价格的影响。
为了实现这一目的,我们可以使用Python等编程语言进行数据分析。以下是一个简单的Python代码示例,用于模拟和比较政策实施前后的股票价格变动:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import
matplotlib.pyplot as plt
#正常显示画图时出现的中文和负号
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
# 假设我们有一组历史股票价格数据
np.random.seed(0)
dates = pd.date_range('20230101', periods=100)
prices = pd.Series(np.random.randn(100).cumsum(), index=dates, name='Price')
# 模拟政策实施前后的股票价格变动
# 假设政策在第50天实施,对股票价格产生了一个固定的正向影响
policy_effect = 5
prices_with_policy = prices.copy()
prices_with_policy.iloc[50:] += policy_effect
# 可视化政策实施前后的股票价格变动
plt.figure(figsize=(10,5))
plt.plot(prices, label='无政策')
plt.plot(prices_with_policy, label='有政策')
plt.title('模拟政策对股价的影响')
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.show()
# 使用统计模型来估计政策对股票价格的影响
# 这里我们简单使用线性回归模型进行估计
X = sm.add_constant(np.arange(len(prices)))
model = sm.OLS(prices_with_policy, X).fit()
policy_impact_estimate = model.params[1] * 50 # 假设政策在第50天实施,计算总影响
print(f'估计政策对股价的影响: {policy_impact_estimate:.2f}')
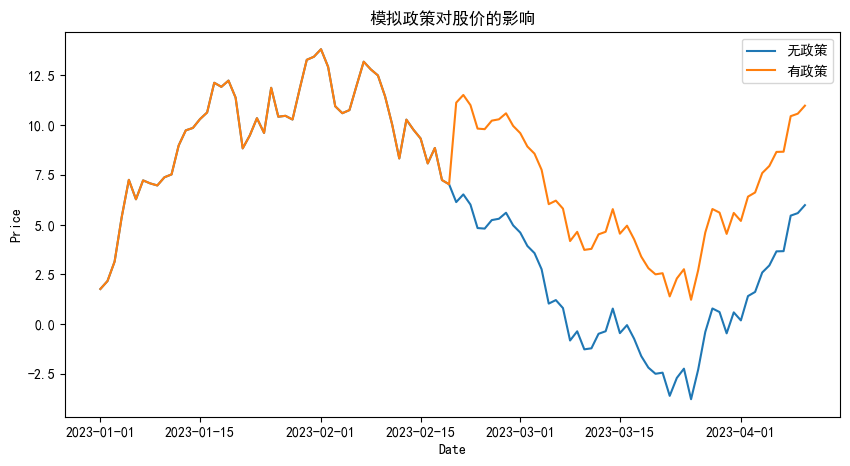
估计政策对股价的影响: -2.14
自助法和基于模拟的推断(Bootstrapping & Simulation-based inference)是用于根据样本对总体进行推断的统计方法。自助法是一种非参数重抽样方法,涉及从原始数据中抽取有放回的随机样本。这样做是为了估计统计量的抽样分布,如均值或标准差,并为统计量构建置信区间。基于模拟的推断是一种更广泛的方法,它使用模拟来对数据集或模型进行推断。这可能涉及从模型中重抽样或创建复制的数据集,并且通常用于常规分析方法不适用或数据复杂的情况。一些例子包括置换检验、参数自助法和基于模拟的校准。自助法和基于模拟的推断都依赖于计算方法和足够的计算资源。近几十年来计算能力的提高使这些方法得到了更广泛的应用,并允许进行更复杂和准确的推断。
自助法和基于模拟的推断在金融量化领域具有广泛的应用,尤其在处理复杂数据集和进行统计推断时显得尤为重要。这些方法允许研究人员在不依赖严格分布假设的情况下,对金融资产的收益率、风险或其他金融指标进行推断。下例如,假设我们有一个包含某股票历史收益率的样本数据集,我们想要估计该股票未来收益率的置信区间。我们可以使用自助法从原始数据中抽取有放回的随机样本,计算每个样本的收益率均值,并根据这些均值构建置信区间。
以下是一个Python代码示例,演示如何使用自助法来估计股票收益率的置信区间:
import numpy as np
# 假设我们有一个包含股票历史收益率的数组
historical_returns = np.array([0.01, 0.02, -0.01, 0.03, 0.01, -0.02, 0.02, 0.01])
# 设置自助法的样本大小
num_samples = 1000
bootstrap_samples = np.random.choice(historical_returns,
(num_samples, len(historical_returns)), replace=True)
# 计算每个自助样本的收益率均值
bootstrap_means = np.mean(bootstrap_samples, axis=1)
# 计算置信区间
alpha = 0.05
lower_bound = np.percentile(bootstrap_means, 100 * alpha / 2)
upper_bound = np.percentile(bootstrap_means, 100 * (1 - alpha / 2))
print(f"置信区间: [{lower_bound:.4f},
{upper_bound:.4f}]")
置信区间: [-0.0025, 0.0188]
基于模拟的推断是一种更广泛的方法,它使用模拟来对数据集或模型进行推断。在金融量化中,这种方法常用于评估投资策略的性能、进行风险管理或定价复杂金融产品。
例如,我们可以使用基于模拟的推断来评估一个投资组合在不同市场条件下的表现。我们可以模拟不同的市场情景,并计算投资组合在这些情景下的收益率和风险。通过比较模拟结果与实际情况,我们可以对投资组合的性能进行更准确的推断。
以下是一个Python代码示例,演示如何使用基于模拟的推断来评估投资组合的性能:
import numpy as np
# 假设我们有两个资产的历史收益率
asset1_returns = np.array([0.02, 0.01, -0.01, 0.04])
asset2_returns = np.array([0.01, 0.03, -0.02, 0.02])
# 设置投资组合的权重
portfolio_weights = np.array([0.5, 0.5])
# 模拟不同的市场情景
num_scenarios = 1000
simulated_returns = np.random.normal(loc=0, scale=0.02, size=(num_scenarios, len(asset1_returns)))
simulated_asset1_returns = simulated_returns + np.mean(asset1_returns)
simulated_asset2_returns = simulated_returns + np.mean(asset2_returns)
# 计算投资组合的模拟收益率
simulated_portfolio_returns = portfolio_weights[0] * simulated_asset1_returns + portfolio_weights[1] * simulated_asset2_returns
# 评估投资组合的性能
portfolio_performance = np.mean(simulated_portfolio_returns, axis=1)
print(f"投资组合的模拟平均收益率: {np.mean(portfolio_performance):.4f}")
print(f"投资组合的模拟标准差: {np.std(portfolio_performance):.4f}")
投资组合的模拟平均收益率: 0.0125
投资组合的模拟标准差: 0.0099
过度参数化模型与正则化((Over-parameterized Models & Regularization))是指具有大量参数的模型,有时参数的数量甚至多于数据点的数量。这些模型通常通过某种形式的正则化进行拟合,正则化通过对模型参数施加约束来防止过拟合。正则化可以作为模型参数或预测曲线的惩罚函数来实现,并有助于通过限制模型的灵活性来确保模型不会过度拟合数据。过度参数化模型的例子包括样条、高斯过程、分类和回归树、神经网络和支持向量机。这些模型的优点是能够捕捉数据中的复杂模式,但如果正则化不当,有时也容易过拟合。近年来,强大的计算资源的发展使得这些模型的拟合和正则化更加有效,从而使其在深度学习(如图像识别)中得到了广泛的应用。研究人员还开发了用于调整、适应和组合过度参数化模型的多个拟合推断的方法。这些方法包括堆叠、贝叶斯模型平均、提升、梯度提升和随机森林,它们有助于提高这些模型预测的准确性和稳健性。总的来说,过度参数化模型和正则化是进行预测和理解复杂数据集的有力工具,在统计学和数据科学领域中变得越来越重要。
过度参数化模型与正则化在金融量化领域同样扮演着至关重要的角色。在金融市场中,数据往往充满噪声且非线性,而过度参数化模型因其能够捕捉数据中的复杂模式而备受青睐。然而,这些模型的强大拟合能力也带来了过拟合的风险,特别是在数据量相对较少或信号较弱的情况下。因此,正则化技术在金融量化中显得尤为重要,它有助于在保持模型复杂性的同时防止过拟合。
在金融量化中,过度参数化模型的应用非常广泛。例如,神经网络可以用于预测股票价格、市场走势或信用违约等复杂金融事件。支持向量机(SVM)则常用于分类任务,如识别欺诈交易或预测资产类别的表现。而这些模型的成功应用往往离不开正则化技术的支持。
正则化技术有多种形式,其中最常见的是L1正则化(也称为Lasso回归)和L2正则化(也称为岭回归)。L1正则化通过惩罚模型参数的绝对值来鼓励稀疏性,即使得部分参数为零,从而降低模型的复杂性。L2正则化则通过惩罚模型参数的平方值来平滑参数,防止参数过大导致过拟合。
以下是一个Python代码示例,演示了如何在金融量化中使用L2正则化的线性回归模型来预测股票价格:
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 假设我们有一个包含历史股票价格和其他相关特征的DataFrame
data = pd.DataFrame({
'price': np.random.randn(100).cumsum(),
'feature1': np.random.randn(100),
'feature2': np.random.randn(100),
# 可以添加更多特征
})
# 将数据分为训练集和测试集
X = data[['feature1', 'feature2'
]] # 特征矩阵
y = data['price'] # 目标变量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 使用L2正则化的线性回归模型进行拟合
ridge = Ridge(alpha=1.0) # alpha是正则化强度
ridge.fit(X_train, y_train)
# 在测试集上进行预测并评估性能
y_pred = ridge.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f'测试集上的均方误差: {mse:.2f}')
测试集上的均方误差: 7.15
多层建模(Multilevel Models)是一种用于分析分层数据的统计方法,其中观测值被分组到更高层次的单位中。这种方法允许对组内和组间变异进行建模,并且对于分析观测单位彼此嵌套的数据非常有用。多层模型的一个例子是一个用于预测学生考试成绩的模型,该模型基于各种因素,如班级规模、教师经验和学校资源。在这个例子中,数据被结构化成不同的组,如学校和教室。多层模型可用于预测每个教室的学生考试成绩,同时考虑诸如班级规模和教师经验等因素。这将使模型能够通过适应每个教室的具体特征来做出更准确的预测。该模型还可用于对影响学生考试成绩的因素进行推断,例如班级规模与教师经验之间的关系。多层模型已被应用于动物育种、心理学、药理学和调查抽样等领域,并且已经得到了几位研究人员的数学结构和证明。如今,多层模型在统计学和数据科学中得到了广泛的应用,并且是结合不同信息来源并从结构化数据中做出推断的宝贵框架。
多层建模(Multilevel Models),在金融量化领域同样展现出了其强大的应用能力。金融数据往往具有多层次的特性,比如不同市场、不同资产类别、不同公司或不同时间点等,这些都构成了数据的不同层次。多层模型能够很好地处理这种分层结构,允许我们在不同层级上进行建模和推断,从而更准确地理解和预测金融现象。
在金融量化中,多层模型的一个典型应用是预测投资组合的风险和收益。我们可以将投资组合中的不同资产视为第一层数据,将不同的资产类别或市场作为第二层数据,甚至还可以考虑宏观经济因素作为更高层次的数据。通过多层模型,我们可以同时考虑资产层面的特性(如波动率、相关性等)和资产类别或市场层面的特性(如行业周期、市场情绪等),以及宏观经济因素的影响,从而更全面地评估投资组合的风险和收益。
以下是一个Python代码示例,演示了如何使用多层模型(这里以线性混合效应模型为例)来预测投资组合中不同资产的收益:
import pandas as pd
import statsmodels.formula.api as smf
import warnings
# 禁用所有警告信息
warnings.filterwarnings('ignore')
# 这里可以是你的代码,警告信息现在不会被打印出来
# 假设数据框已经正确创建
data = pd.DataFrame({
'asset_id': ['A', 'B', 'C', 'D', 'E'],
'category': ['Tech', 'Finance', 'Tech', 'Health', 'Finance'],
'market': ['US', 'US', 'EU', 'US', 'EU'],
'returns': [0.05, 0.02, 0.07, 0.03, 0.01], # 更改列名
'market_cap': [100, 150, 80, 120, 90],
'volatility': [0.2, 0.1, 0.3, 0.15, 0.1]
})
# 使用更改后的列名
model = smf.mixedlm("returns ~ market_cap + volatility", data, groups="category")
result = model.fit()
# 输出模型结果
print(result.summary())
Mixed Linear Model Regression Results
========================================================
Model: MixedLM Dependent Variable: returns
No. Observations: 5 Method: REML
No. Groups: 3 Scale: 0.0000
Min. group size: 1 Log-Likelihood: 5.0865
Max. group size: 2 Converged: No
Mean group size: 1.7
--------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
--------------------------------------------------------
Intercept -0.034 0.016 -2.199 0.028 -0.065 -0.004
market_cap 0.000 0.000 1.464 0.143 -0.000 0.000
volatility 0.314 0.003 112.040 0.000 0.309 0.320
category Var 0.000
========================================================
在这个例子中,我们使用了statsmodels库中的mixedlm函数来拟合一个线性混合效应模型。我们将资产收益作为因变量,资产市值和波动率作为自变量,同时考虑资产类别作为分组变量。通过这个模型,我们可以同时估计出资产层面和资产类别层面的效应,从而更准确地预测不同资产的收益。
多层模型在金融量化中的应用非常广泛,不仅可以用于预测投资组合的风险和收益,还可以用于分析市场趋势、评估资产定价的合理性、研究投资者行为等多个方面。随着金融数据的不断积累和计算能力的提升,多层模型在金融量化中的应用将会越来越广泛和深入。
通用计算算法(Generic Computation Algorithms)是解决统计问题并从数据中做出推断的数学工具。这些算法的例子包括EM算法、Gibbs采样器和变分推断。这些算法利用统计模型的条件独立性结构来提高计算效率。这些算法的主要优点之一是,它们允许开发复杂的统计模型,而不需要对底层计算进行重大更改。这意味着研究人员和分析师可以专注于开发模型本身,而不必担心计算将如何执行的细节。例如,一个统计模型使用EM算法来找到参数的最大似然估计。它通过基于数据迭代更新参数的估计值,直到达到收敛点来实现这一点。这允许研究人员快速有效地找到最适合数据的参数值,而不必担心底层计算的细节。总的来说,通用计算算法的进步在推动复杂统计模型的开发方面发挥了至关重要的作用。它们还使得能够从大型和复杂的数据集中提取有用的见解。
通用计算算法在金融量化领域的应用非常广泛,特别是在处理复杂的数据分析和模型构建时。金融量化分析涉及使用数学和统计方法来建模金融市场的行为,并据此做出预测或投资决策。在这个领域,算法的效率和准确性至关重要。以下是几种通用计算算法在金融量化中的应用,以及如何使用Python来实现这些算法的一个示例。
EM算法(期望最大化算法)
EM算法常用于金融量化中,特别是在处理有缺失数据或隐含变量的模型时。例如,在估算资产价格的隐含波动率或分析投资组合的隐含风险时,EM算法可以提供有效的参数估计。假设我们需要估计一个正态分布的参数,但只能观察到部分数据。我们可以使用EM算法来估计均值和方差。
import numpy as np
def em_algorithm(data, iterations=100):
# 将None替换为np.nan
data = np.where(data == None, np.nan, data)
# 初始化参数
mu = np.nanmean(data)
sigma = np.nanstd(data)
for _ in range(iterations):
# E步骤:计算期望
expected_data = data if data is not None else mu
# M步骤:最大化似然函数更新参数
mu = np.nanmean(expected_data)
sigma = np.nanstd(expected_data)
return mu, sigma
# 示例数据
data = np.array([1, 2, 3, None, 5])
mu, sigma = em_algorithm(data)
print(f"Estimated mean: {mu}, Estimated std: {sigma}")
Estimated mean: 2.75, Estimated std: 1.479019945774904
Gibbs采样器。
Gibbs采样器是一种用于贝叶斯推断的马尔可夫链蒙特卡洛方法(MCMC)。在金融量化中,它可用于估计复杂的后验分布,如资产收益的多变量分布。
import numpy as np
def gibbs_sampler(data, iterations=1000):
samples = np.zeros(iterations)
for i in range(iterations):
# 假设我们有一个简单的条件分布
if i == 0:
samples[i] = data[0]
else:
# 基于前一个样本的条件分布
samples[i] = np.random.normal(samples[i-1], 1)
return samples
# 示例数据
data = np.array([0])
samples = gibbs_sampler(data)
#print(samples)
自适应决策分析是一个研究领域,专注于在复杂、不确定的环境中做出决策。该领域使用统计学、决策理论和心理学工具来帮助个人和组织做出更有效的决策。自适应决策分析的一个重要发展是贝叶斯优化,这是一种使用贝叶斯统计来更新对可能解决方案的信念的方法,基于先前决策的结果来找到问题的最佳解决方案。这在许多情况下都很有用,例如决定开发哪种产品或运行哪种营销活动。自适应决策分析的另一个重要发展是强化学习,这是一种机器学习类型,涉及通过奖励做出好决策和惩罚做出坏决策来训练算法做出决策。例如,这可以用于训练计算机玩像国际象棋或围棋这样的游戏,让它与自己练习并从错误中学习。总的来说,自适应决策分析是一个迅速发展的领域,正在帮助个人和组织在广泛的背景下做出更好的决策。
自适应决策分析在金融量化领域的应用尤为广泛,它可以帮助金融机构和投资者在高度不确定的市场环境中做出更加精准和高效的决策。金融量化通常涉及大量的数据处理和复杂的数学模型,而自适应决策分析能够提供一种动态的、基于数据反馈的决策框架。
贝叶斯优化是一种强大的工具,可用于金融量化策略的参数优化。例如,在开发一个基于机器学习的股票交易策略时,可能存在多个可以调整的参数(如交易信号的阈值、持仓时间等)。贝叶斯优化可以帮助我们找到这些参数的最佳组合,以最大化策略的预期回报。假设我们有一个简单的股票交易策略,其性能取决于两个参数param1和param2。我们可以使用BayesianOptimization库来找到这些参数的最佳值。
#注意,要先pip install bayesian-optimization安装
from bayes_opt import BayesianOptimization
import numpy as np
# 假设的策略性能函数
def stock_trading_strategy(param1, param2):
# 这里应该是一个复杂的模型,但为了简化,我们使用一个简单的函数
return -param1**2 - (param2-1)**2 + 1 # 最大化此函数
# 设置参数的范围
param_bounds = {'param1': (-2, 2), 'param2': (-2, 3)}
# 初始化贝叶斯优化对象
optimizer = BayesianOptimization(
f=stock_trading_strategy,
pbounds=param_bounds,
random_state=1,
)
# 执行优化
optimizer.maximize(
init_points=2,
n_iter=10,
)
# 打印最优参数
print("最优参数:", optimizer.max)
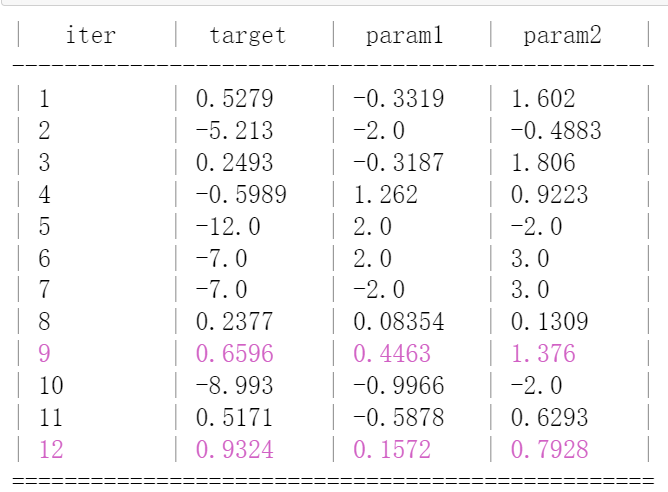
稳健推断(Robust Inference)是一种统计方法,专注于从表现不佳或可能违反所使用统计模型假设的数据中做出推断。这种方法基于一个理念,即即使统计模型的假设没有得到完全满足,只要它们被设计成对这些假设的各种可能违反情况具有稳健性,那么这些模型仍然可以是有用的。稳健推断的一个例子是在回归分析中使用稳健标准误。这种技术调整了回归系数的标准误,以考虑回归模型假设可能未得到完全满足的情况。这可以提供关于数据中变量之间关系的更准确推断。稳健推断的另一个例子是部分识别,这是一种在统计模型的参数无法从数据中完全识别时对这些参数做出推断的方法。这通常用于经济学领域,因为数据生成过程可能不需要完全已知或理解。总的来说,稳健推断是现代统计学中的一个重要概念,因为它允许研究人员开发和使用对实践中可能无法完全满足的假设不太敏感的统计模型和方法。
稳健推断在金融量化领域具有极其重要的应用价值。金融数据往往受到噪声、异常值、非正态分布以及市场微观结构等多种因素的影响,这些因素可能导致传统的统计模型和方法产生误导性的结果。因此,采用稳健推断方法可以帮助金融分析师和量化投资者更好地处理这些挑战,从复杂且可能表现不佳的数据中提取有价值的信息。
(1)稳健回归分析。在金融量化中,回归分析是一种常用的工具,用于研究资产价格、收益率、宏观经济指标等变量之间的关系。然而,金融数据往往违反传统回归分析的假设,如正态性、同方差性和独立性。因此,使用稳健标准误(如HC标准误或White标准误)来调整回归系数的标准误,可以提供更加准确和可靠的推断。
(2)部分识别方法。在金融模型中,参数的完全识别通常是一个挑战。例如,在资产定价模型中,风险溢价或预期收益率的参数可能无法从数据中直接估计。部分识别方法允许研究人员在参数无法完全识别的情况下,仍然能够对这些参数的可能范围进行推断,从而为金融决策提供有用的信息。
(3)稳健优化。在金融量化策略中,优化问题(如资产配置、投资组合选择等)常常需要处理不确定性和模型风险。稳健优化方法考虑了模型参数的不确定性,并寻求在参数的各种可能实现下都能表现良好的解决方案。
以下是一个使用statsmodels库进行稳健回归分析的Python代码示例。我们将使用HC标准误来调整回归系数的标准误。
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
# 设置随机种子以便结果可复现
np.random.seed(42)
# 生成模拟数据
n = 100 # 样本大小
x1 = np.random.normal(0, 1, n) # 自变量x1
x2 = np.random.normal(0, 1, n) # 自变量x2
y = 2 * x1 + 3 * x2 + np.random.normal(0, 2, n) # 因变量y,带有一些噪声
# 将数据放入Pandas DataFrame中
df = pd.DataFrame({
'y': y,
'x1': x1,
'x2': x2
})
# 使用statsmodels的RLM类进行稳健回归
model = smf.rlm("y ~ x1 + x2", data=df).fit()
# 打印回归结果
print(model.summary())
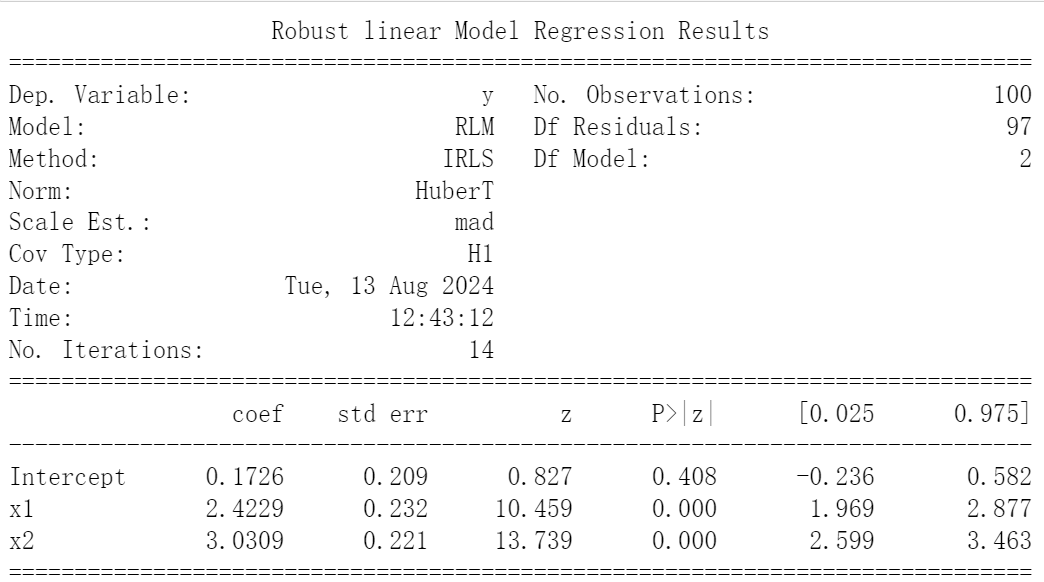
在这个例子中,我们首先生成了两个自变量x1和x2,它们都是从标准正态分布中抽取的。然后,我们生成了因变量y,它是x1和x2的线性组合,再加上一些正态分布的噪声。最后,我们使用statsmodels的RLM类进行稳健回归分析,并打印出回归结果。
稳健回归分析在这里特别有用,因为金融数据往往包含异常值或噪声,这些可能违反传统回归分析的假设。通过使用稳健标准误,我们可以更好地处理这些数据中的不确定性,并获得更加准确和可靠的回归系数估计。
探索性数据分析(Exploratory Data Analysis,简称EDA)是一种统计方法,侧重于使用图形技术来理解和总结数据,而不是仅依赖数学方程和正式的统计检验。这种方法强调了开放式探索和交流的重要性,并且经常用于发现数据中可能并不立即明显的模式和趋势。探索性数据分析背后的一个关键理念是使用图形技术来可视化数据。这些技术可以包括直方图、散点图和箱线图,并且经常用于快速识别数据中的趋势和模式。例如,直方图可以用于可视化定量变量的分布,而散点图可以显示两个定量变量之间的关系。探索性数据分析的另一个重要方面是统计图形的使用,这是数据的视觉展示,利用数据本身的结构来帮助读者理解数据。这些图形可以快速有效地传达数据中的复杂模式和趋势,并且经常用于帮助研究人员和分析师理解大型和复杂的数据集。总的来说,探索性数据分析是一种重要的数据分析方法,它强调了图形可视化和开放式探索在理解和总结数据中的重要性。
探索性数据分析(EDA)是一种非形式化的数据分析方法,旨在通过图形、统计摘要等手段对数据的特征进行初步了解,以便发现数据中的模式、趋势和异常值,为后续的数据处理和建模奠定基础。在金融量化领域,EDA尤为重要,因为它可以帮助分析师理解复杂的金融市场数据,识别交易机会和风险。
探索性数据分析的一般步骤:
单变量分析:
双变量分析:
多变量分析:
假设检验和模型探索:
报告和可视化:
下面推荐一款强大的EDA可视化分析工具dtale。dtale是一个基于Python的开源工具,提供了一个交互式的Web界面,使用户能够轻松地在浏览器中查看和分析数据集,包括生成数据集的摘要统计信息、支持多种图表和可视化方式、提供数据过滤和排序功能、内置处理缺失值的选项、支持数据导出为常见格式,以及集成高级分析功能等。它简化了数据分析的流程,提高了分析效率和准确性。
#pip install dtale
import qstock as qs
import dtale as dt
df=qs.get_data('sh')
dt.show(df)
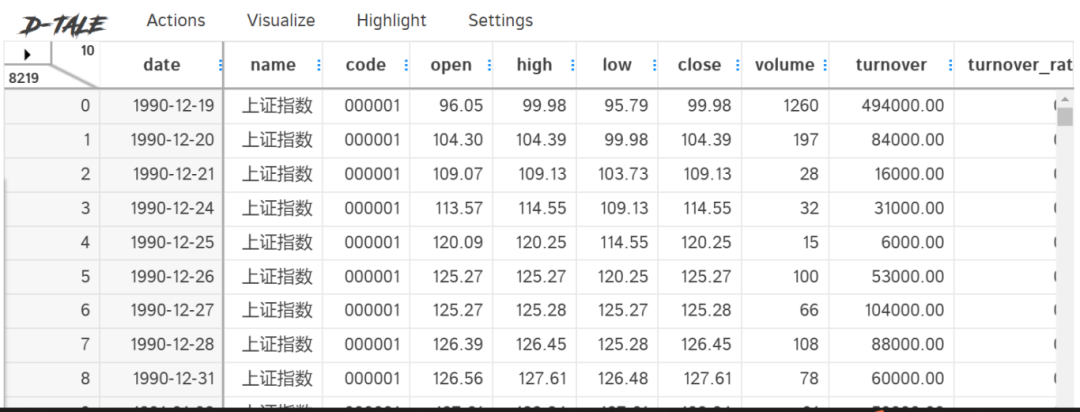
关于dtale的详细应用留给读者自己探索。
参考资料:Benedict Neo. The 8 Most Important Statistical Ideas of the Past 50 Years. Mediam. 2023