卡方检验（Chi square test）是一种统计方法，用于检验观察数据与期望数据之间的差异是否具有显著性。它用于分析分类数据，评估变量之间的关联性，以及判断实际观测结果与理论预期是否一致。卡方检验在医学、产品设计、工程以及各种研究项目中被广泛应用，帮助决策者确定数据中的显著差异并做出科学的决策。

有关统计检验的概念，可以参考：《一文带您了解统计假设检验:几种常见的显著性检验方法》。

卡方检验统计量的逐步计算过程

让我们通过数据实例来了解卡方检验的具体计算步骤。使用摸您COVID数据。我们将使用卡方检验来查看某些COVID症状与是否进入ICU之间是否存在关联。

示例数据

假设我们有以下数据，显示了100位COVID患者中，出现特定症状（如咳嗽、发烧）和是否进入ICU的情况：

步骤1：构建假设

• 原假设（H0）：症状与是否进入ICU无关。

• 备择假设（H1）：症状与是否进入ICU有关。

步骤2：计算期望频数

根据原假设，计算期望频数：

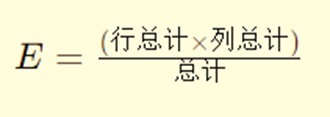
例如，有症状且进入ICU的期望频数：

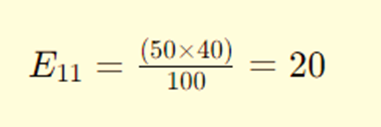
对每个单元格进行类似的计算：

步骤3：计算卡方统计量

使用以下公式计算卡方统计量：

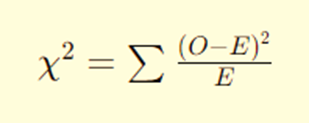
其中，O是观察频数，E是期望频数。

对于每个单元格进行计算：

将所有单元格的结果相加后，χ2为16.66

步骤4：确定自由度并查表

自由度（df）计算公式为：

df=(行数−1)×(列数−1)=1

步骤5：查找临界值

查找卡方分布表中对应自由度和显著水平（通常为0.05）的临界值。例如，对于df = 1，显著水平为0.05，临界值约为3.84。

步骤6：做出决策

比较计算的卡方统计量与临界值：

16.66>3.84

因为计算的卡方值大于临界值，我们拒绝原假设，这意味着症状与是否进入ICU之间存在显著关联。

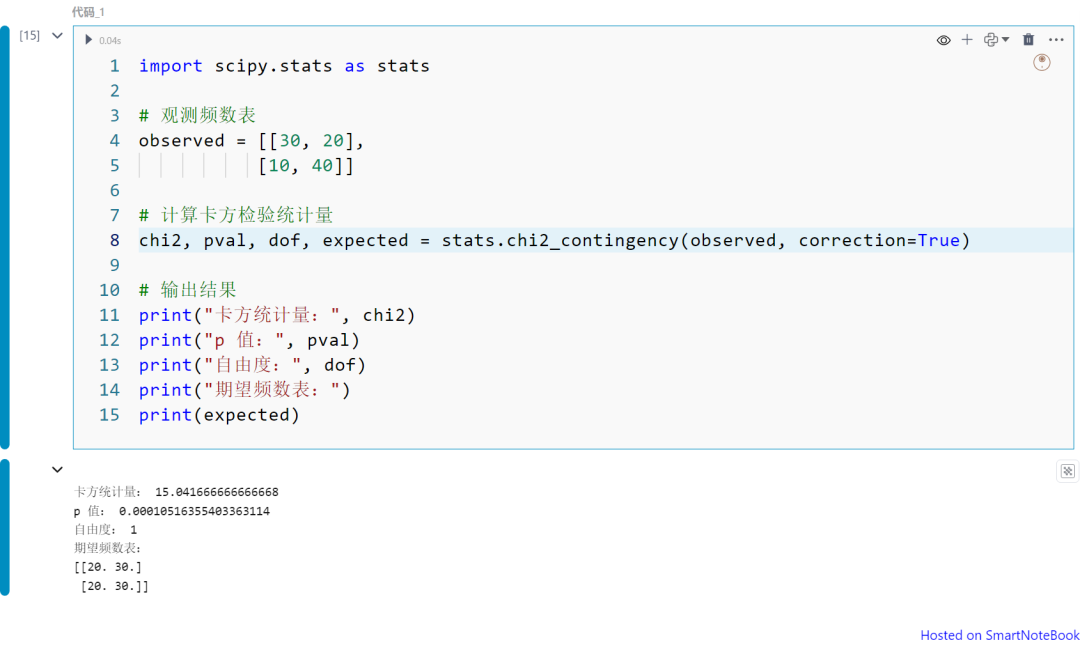
Python  卡方检验示例

import scipy.stats as stats
# 观测频数表observed = [[30, 20],           [10, 40]]
# 计算卡方检验统计量chi2, pval, dof, expected = stats.chi2_contingency(observed, correction=False)
# 输出结果print("卡方统计量：", chi2)print("p 值：", pval)print("自由度：", dof)print("期望频数表：")print(expected)

• 特别注意参数correction：是否进行校正（默认为 True）

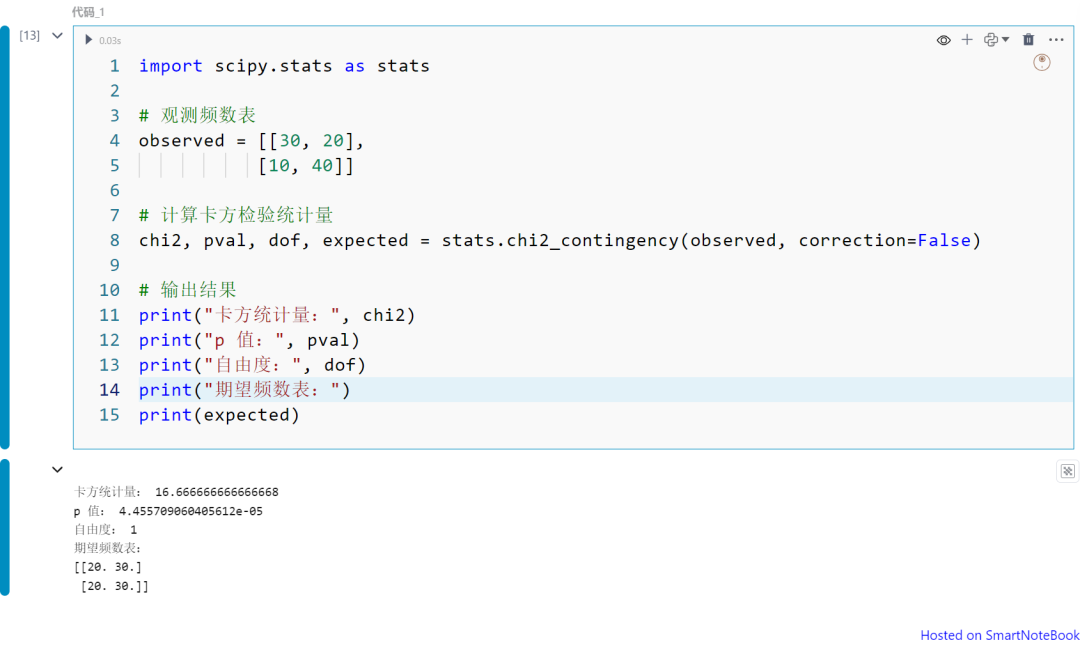
如果 correction 为 True，则会对卡方统计量进行 Yates 校正，以提高小样本数据的准确性。

上面的代码为correction=False 的情况下，没有进行校正，与手工计算的结果是一种；如果改成True，小样本的情况校正后变小。

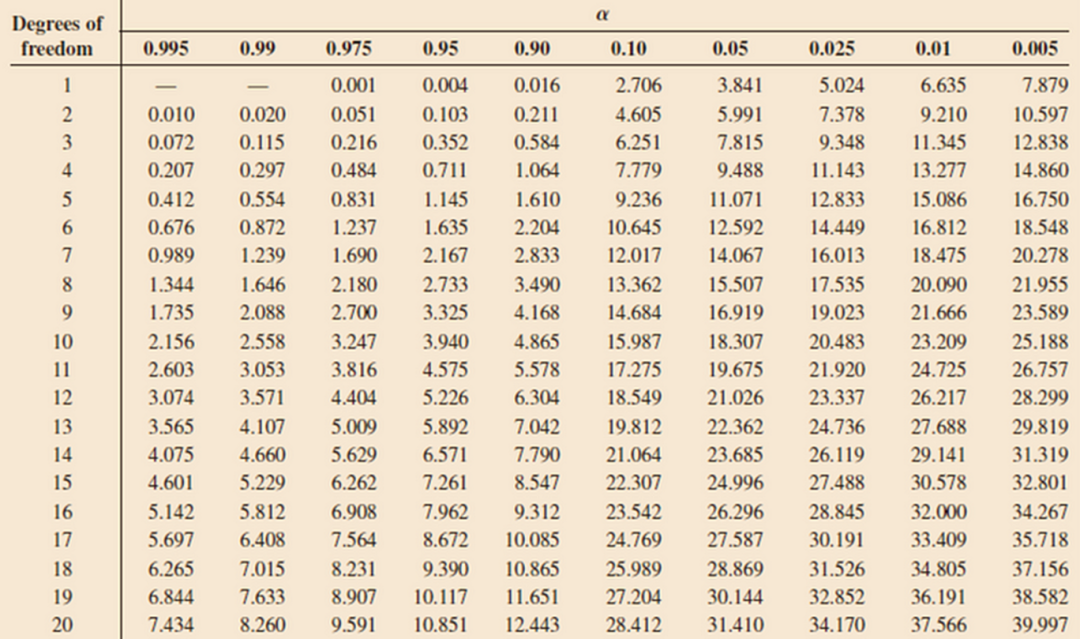
卡方概率表

下面是一张学校教材上卡方概率表。此表中的值不是 p 值。它们是基于不同自由度和 alpha 的卡方分布的检验统计量。你需要将计算出的检验统计量与此表中的数字进行比较。

卡方检验（Chi square test）是一种广泛应用于统计分析的方法，用于确定观察数据与期望数据之间是否存在显著差异，特别是在分析分类数据和评估变量之间的关联性时。它在医学、产品设计、工程以及各种研究项目中都扮演着重要角色，帮助决策者基于科学数据做出准确的判断和决策。