本文目录

1 MaskGIT：非自回归的掩码图像生成 Transformer
(来自谷歌)
1 MaskGIT 论文解读
1.1 MaskGIT 的诞生背景
1.2 MaskGIT 两阶段策略
1.3 迭代解码
1.4 掩码策略设计
1.5 图像生成实验结果
1.6 图像编辑应用

太长不看版

在计算机视觉领域中，生成式 Transformer 技术一直都在经历着迅速的迭代，因为其在合成高保真和高分辨率图像方面能力出众。在当时，最好的生成式 Transformer 技术仍将图片视为 token 序列，并且根据光栅扫描顺序 (即逐行) 顺序解码图像。这就很像语言模型的解码方式，即：视图像为 1D 信号，按照光栅顺序来解码。

本文认为，这种范式不是最优的，而且效率也不高。本文提出一种使用 Bi-directional 注意力机制的 Transformer 解码器的新型图像生成范式，称之为 MaskGIT。在训练期间，首先把输入图片进行一些随机的掩码 (mask)，并且使得 MaskGIT 来学习 mask 掉的值；在推理期间，MaskGIT 模型同时生成图像的所有 token，并不断迭代直至生成好看的图像。

本文实验表明，MaskGIT 在 ImageNet 数据集上显着优于最先进的 Transformer 模型，相比自回归解码的速度，提高了多达 64 倍。此外，MaskGIT 可以很容易地扩展到各种图像编辑任务，例如修复、外推和图像处理。

本文做了哪些具体的工作

1. 第一个证明掩码图像建模在 ImageNet benchmark 上是成立的。提出了一种新的掩码图像 Transformer 范式，使用 Bi-directional Transformer 来进行图像生成。在训练期间，MaskGIT 使用类似于 BERT 的掩码预测的完形填空任务上进行训练。在推理期间，MaskGIT 采用非自回归解码方法，以恒定步数合成图像。MaskGIT 的解码速度比自回归解码快一个数量级，比如图 2 只需要 8 步，而标准自回归解码则需要 256 步。
2. ImageNet class-conditional generation 的 256×256 和 512 ×512 基准测试中，作者证明 MaskGIT 明显更快，并且比最先进的自回归 Transformer (VQGAN) 生成更高质量样本，来进行图像生成。即使与当时强劲的 GAN 模型 (BigGAN) 或者 Diffusion model (即 ADM) 相比，MaskGIT 提供了差不多的样本质量，同时产生了更丰富的多样性。
3. MaskGIT 还适合自回归模型难以胜任的图像操作任务，比如图 1 就是一个新的应用场景：MaskGIT 根据给定的边界框重新生成其内部的内容，同时保持其他部分不变。这个任务对于自回归模型或者 GAN 来说都很难。

1 MaskGIT：非自回归的掩码图像生成 Transformer

论文名称：MaskGIT: Masked Generative Image Transformer (CVPR 2022)

论文地址：

http://arxiv.org/pdf/2202.04200

项目链接：

http://masked-generative-image-transformer.github.io/

1.1 MaskGIT 的诞生背景

近年来，深度图像领域取得了很大的进展。代表性的模型是生成对抗网络 GAN，其能够以惊人的速度合成高保真图像。然而，它们存在众所周知的问题，包括训练不稳定和模式崩溃，导致样本多样性不足。解决这些问题仍然是一个悬而未决的问题。

受 Transformer 和 GPT 在 NLP 中的启发，生成式 Transformer 模型在图像合成方面受到越来越多的关注。这些方法旨在将像序列这样的图像建模，并利用现有的自回归模型生成图像。这类方法一般可以分为2步：

1. 将图像量化为一系列离散 tokens (或者叫做 visual words)。
2. 训练自回归模型 (例如 Transformer) 根据先前生成的结果顺序生成图像 tokens，即自回归解码。

与 GAN 中使用的细微 min-max 优化不同，这些模型是通过最大似然估计学习的。由于设计差异，现有的工作已经证明了它们在提供稳定的训练和改进的分布覆盖或多样性方面优于 GAN。

现有的生成式 Transformer 的工作主要集中在第1阶段，即如何量化图像，使信息丢失最小化，而对于第2阶段的建模，一般还是使用 NLP 的自回归方法。因此，即使是最先进的生成式 Transformer 仍然将图像视为序列，其中图像按照光栅扫描顺序被展平为一维 token 序列，即从左到右逐行扫描。

作者认为这种表征对于图像来讲，既不是最佳的也不是最有效的。因为图片与文本不同，它不是顺序的。此外，将图像视为平面序列意味着自回归序列长度呈二次方增长，这就很容易形成一个非常长的序列，这个长度比任何自然语言的文本句子都长。这对长序列建模提出了挑战，而且使得解码过程更具有挑战性。比如，在 GPU 上生成单个图像的 32×32 的 tokens 需要相当大的 30 秒。

1.2 MaskGIT 两阶段策略

第1阶段和 VQGAN 相同, 通过 Encoder 把图片 变为 latent embedding 。再通过 codebook 把这些 embedding 量化为视觉 tokens。

对于第2阶段，本文提出掩码视觉 token 建模 (Masked Visual Token Modeling, MVTM)。

令 为将图像输入到 VQ Encoder 得到的 latent tokens, 其中 token 矩阵的长度, 为对应的二进制掩码。在训练期间, 对 tokens 的子集进行采样, 并用特殊的 [MASK] token 替换它们。如果 , 则 token 被替换为 [MASK], 否则, 当 时, 将保持不变。

设置一个 mask scheduling function , 每次在0和1之间采样一个 ratio, 然后均匀选择 中的 tokens, 在其上面放置 mask。定义放完 mask 之后的结果为 , 训练目标是最小化掩码标记的负对数似然：

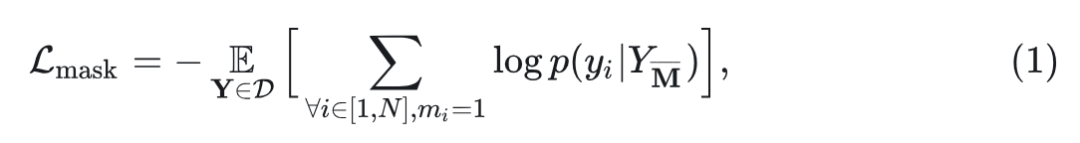
具体来讲, 将掩码 输入到 Bi-directional Transformer 中, 预测每个掩码标记的概率 , 其中负对数似然计算为真实 one-hot token 和预测 token 之间的交叉熵。注意这步与自回归建模的关键区别: MVTM 中的attention 有两个方向, 允许图像关注图像中的所有 token, 以利用更丰富的上下文。

1.3 迭代解码

之前自回归解码的方法里面，生成后面的 token 时候需要前面所有的 tokens 的信息。这个过程不能够并行，因此对于图像而言会非常慢，因为图像 token 序列的长度，一般是 256 或 1024，通常比语言 token 序列大得多。在本文的解码方法中，图像中的所有 token 都是并行生成的。由于 MTVM 的双向自注意力，使得这个过程变得可行。

在理论上，模型能够一次性生成所有的 tokens。但是由于这个过程与训练任务不一致，因此实际使用的时候发现具有挑战性。因此，作者开发了一种迭代解码方法，从空白画布开始，所有 tokens 都被 mask 掉，即 。对于第 tt 步的迭代，算法运行如下：

1. 预测过程： 给定当前迭代步骤 的 masked tokens, 本文模型预测一个 的张量,代表了每个掩码位置的概率值。

2. 采样过程： 在每个位置 , 根据预测概率值 采样一个 , 其对应的预测值被当做置信度的分数。

3. 掩码策略： 计算当前迭代步骤要再 mask 掉多少个 tokens：, 其中 为 mask scheduling function, 为总的迭代数。

4. 掩码： 根据上一步的计算, mask 掉 个 tokens。得到 。第 步的 mask 的计算方法是：

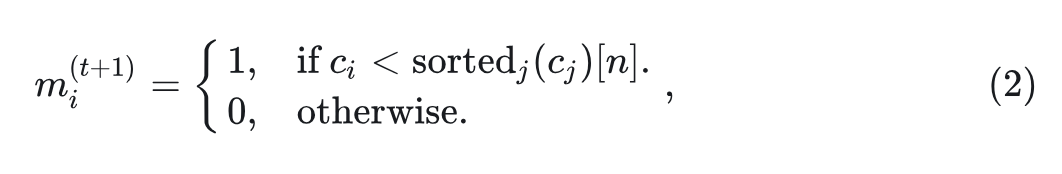
其中, 是第 个 tokens 的置信度分数。

解码算法以 步合成图像。在每次迭代中, 模型同时预测所有 tokens, 但只保留置信度最高的 tokens。剩余的tokens 在下一次迭代中重新预测。掩码的比例逐渐减少，直到所有 tokens 在 次迭代内生成。

1.4 掩码策略设计

作者发现图像生成的质量受到掩码策略的影响很大。作者通过掩码调度函数 对掩码过程进行建模。在推理过程中, 该函数的输入是 , 表示解码过程。在训练期间, 在 中随机采样比率 以模拟解码的场景。

掩码策略函数：首先， 需要是一个介于 0 和 1 之间的连续函数。其次， 应该是对于输入 单调递减, 即满足 。第 2 个属性确保了解码算法的收敛性。

作者尝试了3种掩码策略函数：

• 线性函数是一个简单的解决方案，每次 mask 掉相同数量的 tokens。
• 凹函数捕获了图像生成遵循更少到更多信息流的直觉。一开始，大多数 tokens 被 mask 掉，因此模型只需要对模型感到自信的 token 做出一些预测。凹函数包括余弦函数、平方函数、三次函数和指数函数。
• 凸函数相反是一个预测多到预测少的过程。使得模型需要在前几次迭代中最终实现绝大多数 tokens。凸函数包括平方根函数和对数函数。

1.5 图像生成实验结果

作者在 ImageNet 数据集 256×256 和 512×512 上的标准 class-conditional 图像生成任务上评估 MaskGIT。对于每个数据集都训练一个单独的 autoencoder, decoder, 和 codebook。其中 codebook 的维度是 1024，256×256 的图片通过 Encoder 被下采样 16 倍。作者发现这种自编码器与 codebook 一起可以重用来合成 512×512 的图像。

所有模型都具有相同的配置：24 层、8 个注意力头、768 的 embedding dimension 和 3072 的 hidden dimension。使用 RandomResizeAndCrop 作为数据增强。ImageNet 模型训练了 300 个 epoch，而 Places2 模型训练了 200 个 epoch。

在 ImageNet 256×256 任务中，本文方法在 FID 和 IS 指标上超越了 VQGAN。作者还训练了一个与 MaskGIT 相同的超参数的 VQGAN baseline，以进一步突出 Bi-directional Transformer 和 uni-directional Transformer 之间的差异，发现在这两个分辨率下，MaskGIT 仍然大大优于基线。

而且，MaskGIT 在两种分辨率上都改进了 BigGAN 的 FID，在 512×512 上实现了新的最先进的 FID 7.32。为了评估 MaskGIT 和自回归模型之间的速度差异，作者比较了 MaskGIT 和 VQGAN 的运行时间。如图 5 所示，MaskGIT 显着加速了 30-64× 的 VQGAN，随着图像分辨率（因此输入标记长度）的增长，加速更加明显。

除了样本质量，作者还将分类准确度分数 (CAS) 和 Precision/Recall 视为评估样本多样性的两个指标。CAS 首先仅在候选模型生成的样本上训练 ResNet-50 分类模型，然后在 ImageNet 验证集上测量分类器的分类精度。图 4 中的最后两列显示了 CAS 结果，其中，在真实 ImageNet 训练数据上训练的 ResNet-50 模型的 top-1 和 top-5 精度分别为 76.6% 和 93.1%。对于分辨率 256×256，作者使用数据增强 RandAugment 的常见做法。可以发现，MaskGIT 显着优于先前的工作 VQVAE-2 和 VQGAN，在两种分辨率的 ImageNet 上得到了新的 SOTA CAS 分数。

MaskGIT 的样本相对于 BigGAN 的样本更加多样化，光照、姿势、比例和上下文更加多样化，如图 6 所示。

1.6 图像编辑应用

作者介绍了 MaskGIT 在 3 个图像编辑任务上的直接应用：class-conditional 图像编辑、图像修复和外绘。作者表明，在不修改架构或任何特定于任务的训练的情况下，MaskGIT 能够在所有3个应用上产生比较令人信服的结果。此外，MaskGIT 在图像修复方面都获得了与专用模型相当的性能，即使它不是专门为任一任务设计的。

Class-conditional 图像编辑

作者定义了一个新的 Class-conditional 图像编辑任务来展示 MaskGIT 的灵活性。在这个任务中，模型在保留上下文的同时重新生成给定 class 的边界框内指定的内容，即框外的内容。由于违反预测顺序，自回归方法是不可行的。然而，对于 MaskGIT，如果将边界框区域视为初始掩码到迭代解码算法的输入，这个任务就可以做了。

图像修复： 图像修复或图像补全是合成缺失区域内容的基本图像编辑任务，以便完成在视觉上看起来逼真。作者把 MaskGIT 拓展到了这个领域，将待修复的 mask 解释为初始 mask。为了匹配基线训练，作者在 Places2 数据集的512×512 中心裁剪图像上训练 MaskGIT。所有超参数都与在 ImageNet 上训练的 MaskGIT 模型保持一致。

作者将 MaskGIT 与常见的基于 GAN 的基线进行比较，包括 DeepFillv2 和 HiFill，在具有中心 50%×50% mask 的 impainting 上，在 Places2 验证集上进行评估。如图 8 所示，MaskGIT 在 FID 和 IS 中大大超过了 DeepFill 和 HiFill，同时实现了接近最先进的修复方法 CoModGAN。

图像外推： 图像外推是最近受到越来越多的关注的图像编辑任务。由于周围像素的约束较少，因此预测区域的不确定性更大，因此将其视为比修复更具挑战性的任务。作者比较了常见的基于 GAN 的 baseline，包括 Boundless 、In&Out、InfinityGAN 和 CoModGAN，以 50% 的比例向右外推。如图 8 所示，MaskGIT 击败了所有基线并实现最先进的 FID 和 IS。如图 9 中的示例所示，MaskGIT 也能够在相同输入的情况下合成不同的结果。

不同掩码策略的消融实验结果

作者使用 ImageNet 256×256 上的默认设置进行消融实验。MaskGIT的一个关键设计是训练和迭代解码中使用的掩码策略函数，作者在图 10 中进行了可视化，结果如图 11 所示。可以观察到凹函数通常比线性获得更好的 FID 和 IS，然后才是凸函数。作者使用余弦策略函数作为默认设置。

作者认为凹函数表现好的原因有2点：

1. 训练任务更加困难 (使用相对凸函数更大的 mask 比例进行训练)。
2. 在解码的过程中，一开始预测得少，越到后面预测的 mask 越多。

不同迭代次数的消融实验结果

作者也尝试了不同的掩码策略下，使用不同迭代次数的实验结果，如图 10 所示。在相同的设置下，更多的迭代不一定带来更好的性能：随着 TT 的增加，大部分函数都有个 "sweat point"，其中模型的性能达到峰值。而且，随着函数的凹性越来越低，"sweat point" 也逐渐右移。余弦函数不仅 FID 指标最好，而且有最小的 "sweat point"。作者认为 "sweat point" 的存在是因为过多的迭代次数会阻止模型维持那些不太自信的预测，从而影响其生成 token 的多样性。

公众号后台回复“极市直播”获取100+期极市技术直播回放+PPT