点击上方↑↑↑“OpenCV学堂”关注我
来源:公众号 新智元 授权
【导读】Llama 3发布一个月后,一位开发者在GitHub上创建了名为「从头开始实现Llama 3」的项目,引起了开源社区的广泛关注。代码非常详细地展现了Llama所使用的Transformer架构,甚至让Andrej Karpathy亲自下场「背书」。
Llama系列作为为数不多的优质开源LLM,一直受到开发者们的追捧。在Hugging Face社区的文本生成模型中,几乎是「霸榜」的存在。
就在520这天,一位名叫Nishant Aklecha的开发者在推特上宣布了自己的一个开源项目,名为「从头开始实现Llama 3」。
这个项目详细到什么程度呢——
矩阵乘法、注意力头、位置编码等模块全部都拆开解释。
而且项目全部用Jupyter Notebook写成,小白都可以直接上手运行。
堪比哈佛NLP小组曾经出品的「The Annotated Transformer」。
https://nlp.seas.harvard.edu/annotated-transformer/才一天多的时间,小哥发表的这篇推特已经有32万次阅读,甚至被Andrej Karpathy大佬亲自点赞——
「全部拆开解释之后,通过模块的嵌套以及互相调用,可以更清楚地看到模型到底做了什么。」
项目也在GitHub上获得了4.6k星。
项目地址:https://github.com/naklecha/llama3-from-scratch那就让我们来看看作者是如何深入拆解Llama 3的。
首先需要从Meta官网下载模型权重文件,以便后续运行时使用。
https://github.com/meta-llama/llama3/blob/main/README.md下载后需要先读取权重文件中的变量名:
model = torch.load(
"Meta-Llama-3-8B/consolidated.00.pth")
print(json.dumps(list(model.keys())[:20], indent=4))
[
"tok_embeddings.weight",
"layers.0.attention.wq.weight",
"layers.0.attention.wk.weight",
"layers.0.attention.wv.weight",
"layers.0.attention.wo.weight",
"layers.0.feed_forward.w1.weight",
"layers.0.feed_forward.w3.weight",
"layers.0.feed_forward.w2.weight",
"layers.0.attention_norm.weight",
"layers.0.ffn_norm.weight",
"layers.1.attention.wq.weight",
"layers.1.attention.wk.weight",
"layers.1.attention.wv.weight",
"layers.1.attention.wo.weight",
"layers.1.feed_forward.w1.weight",
"layers.1.feed_forward.w3.weight",
"layers.1.feed_forward.w2.weight",
"layers.1.attention_norm.weight",
"layers.1.ffn_norm.weight",
"layers.2.attention.wq.weight"
]
以及模型的配置信息:
with open("Meta-Llama-3-8B/params.json", "r") as f:
config = json.load(f)
config
{'dim': 4096,
'n_layers': 32,
'n_heads': 32,
'n_kv_heads': 8,
'vocab_size'
: 128256,
'multiple_of': 1024,
'ffn_dim_multiplier': 1.3,
'norm_eps': 1e-05,
'rope_theta': 500000.0}
根据以上输出,可以推断出模型架构的信息——
32个transformer层
每个多头注意力模块有32个注意力头
分词器的词汇量为128256
直接将模型配置信息存储到变量中,方便使用。
dim = config["dim"]n_layers = config["n_layers"]n_heads = config["n_heads"]n_kv_heads = config["n_kv_heads"]vocab_size = config["vocab_size"]multiple_of = config["multiple_of"]ffn_dim_multiplier = config["ffn_dim_multiplier"]norm_eps = config["norm_eps"]rope_theta = torch.tensor(config["rope_theta"])
那么就从语言模型的第一步——分词器开始,但是这一步并不需要我们自己手写。
Llama 3使用了GPT等大模型常用的BPE分词器,karpathy大佬之前就复现过一个最简版。
https://github.com/karpathy/minbpe除了Karapthy大佬复现的版本,OpenAI也开源了一个运行速度很快的分词器tiktoken。这两个随便挑,估计都比自己从头训练的要强。
https://github.com/openai/tiktoken
有了分词器,下一步就是要把输入的文本切分为token。
prompt = "the answer to the ultimate question of life, the universe, and everything is "tokens = [128000] + tokenizer.encode(prompt)print(tokens)tokens = torch.tensor(tokens)prompt_split_as_tokens = [tokenizer.decode([token.item()]) for token in tokens]print(prompt_split_as_tokens)
[128000, 1820, 4320, 311, 279, 17139, 3488, 315, 2324, 11, 279, 15861, 11, 323, 4395, 374, 220]['', 'the', ' answer', ' to', ' the', ' ultimate', ' question', ' of', ' life', ',', ' the', ' universe', ',', ' and', ' everything', ' is', ' ']
再使用PyTorch内置的神经网络模块(torch.nn)将token转换为embedding,[17x1]的token维度变为[17x4096]。
embedding_layer = torch.nn.Embedding(vocab_size, dim)embedding_layer.weight.data.copy_(model["tok_embeddings.weight"])token_embeddings_unnormalized = embedding_layer(tokens).to(torch.bfloat16)token_embeddings_unnormalized.shape
此处应该是整个项目中唯一使用PyTorch内置模块的地方。而且,作者给出了温馨提示——记得经常打印一下张量维度,更容易理解。
之后再使用RMS对embedding进行归一化处理。这一步不会改变张量形状,只是归一化其中的数值,公式如下:

模型配置中的norm_eps变量设置为1e-5,就是用在此处,防止rms值意外设置为0。
def rms_norm(tensor, norm_weights): return (tensor * torch.rsqrt(tensor.pow(2).mean(-1, keepdim=True) + norm_eps)) * norm_weights
每一个Transformer层都需要经过如下步骤:
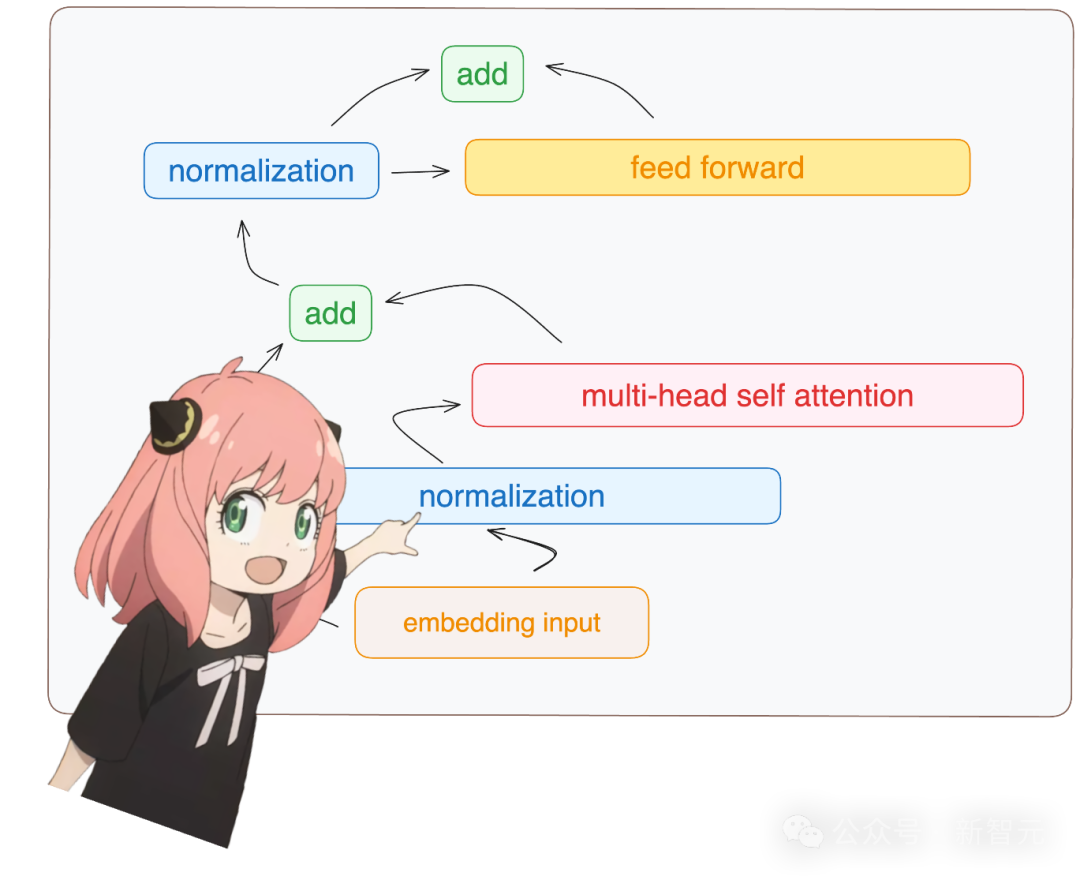
由于是从头构建,我们只需要访问模型字典中第一层(layer.0)的权重。
先用刚才定义的rms_norm函数,结合模型权重,进行embedding的归一化处理。
token_embeddings = rms_norm(token_embeddings_unnormalized, model["layers.0.attention_norm.weight"])token_embeddings.shape
多头注意力
查询向量
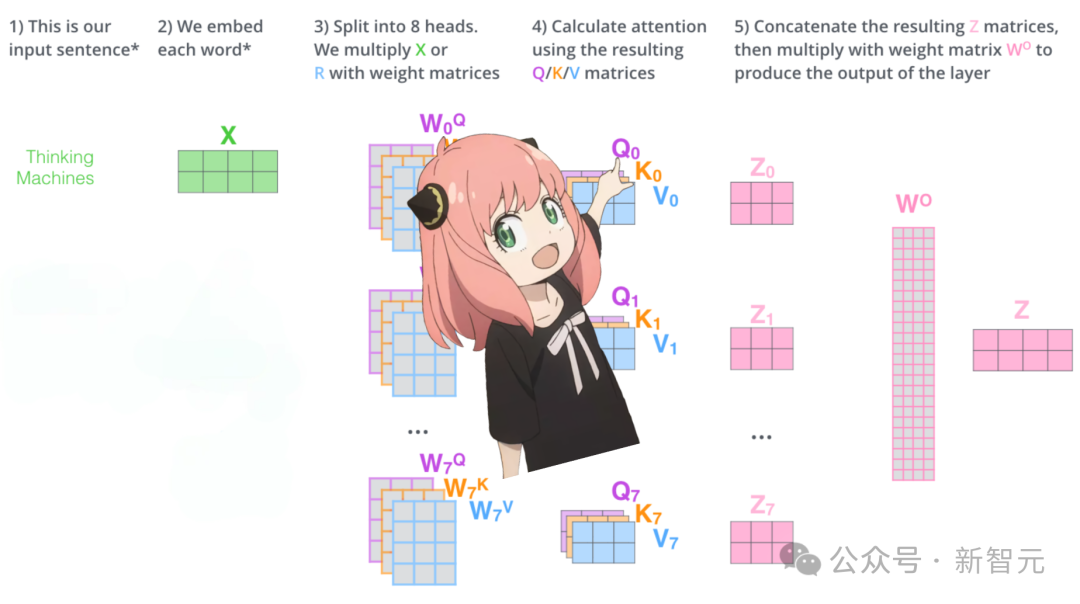
让我们先用一张图复习注意力机制的计算过程:
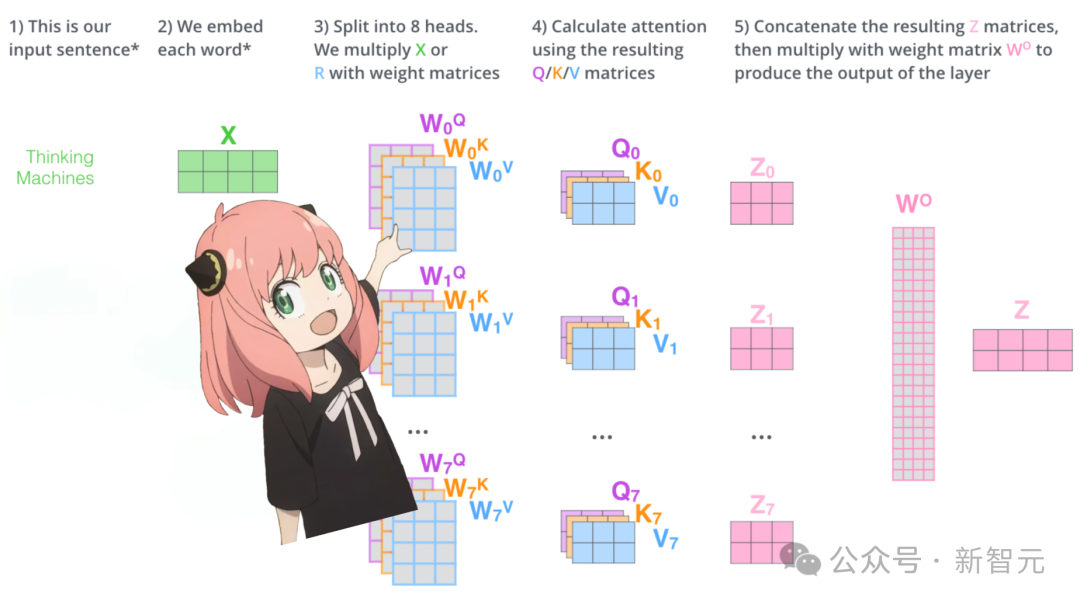
如果从模型直接加载查询、键、值和输出的权重,我们会得到四个二维矩阵,形状分别为 [4096x4096]、[1024x4096]、[1024x4096]、[4096x4096]。
print( model["layers.0.attention.wq.weight"].shape, model["layers.0.attention.wk.weight"].shape, model["layers.0.attention.wv.weight"].shape, model["layers.0.attention.wo.weight"].shape)
torch.Size([4096, 4096]) torch.Size([1024, 4096]) torch.Size([1024, 4096]) torch.Size([4096, 4096])
因为大模型考虑了注意力中乘法并行化的需求,压缩了矩阵维度。但是为了更清楚地展示机制,作者决定将这些矩阵都展开。
模型有32个注意力头,因此查询权重矩阵应该展开为[32x128x4096],其中128是查询向量的长度,4096是embedding的维度。
q_layer0 = model["layers.0.attention.wq.weight"]head_dim = q_layer0.shape[0] // n_headsq_layer0 = q_layer0.view(n_heads, head_dim, dim)q_layer0.shape
torch.Size([32, 128, 4096])
于是可以访问第一个注意力头的查询权重,维度是[128x4096]。
q_layer0_head0 = q_layer0[0]q_layer0_head0.shape
现在将查询权重与embedding相乘,就得到了查询矩阵,维度为[17x128],表示长度为17的句子,其中每个token都有维度为128的查询向量。
q_per_token = torch.matmul(token_embeddings, q_layer0_head0.T)q_per_token.shape
位置编码
由于注意力机制中对每个token没有序列「位置」的概念,第一个词和最后一个词在Q、K、V矩阵看来都是一样的,因此需要在查询向量中嵌入维度为[1x128]的位置编码。
位置编码有多种方法,Llama模型采用的是旋转位置编码(RoPE)。
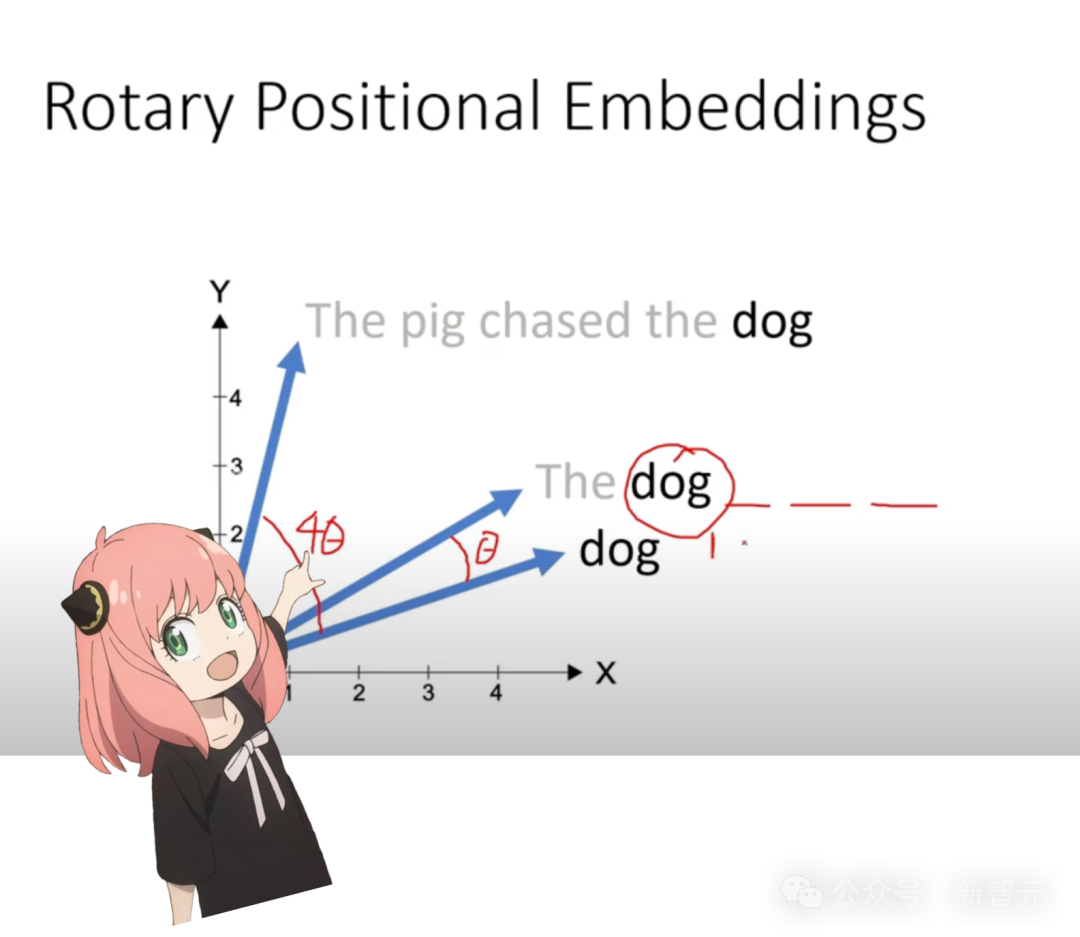
首先将查询向量两两分为一对,共有64对。
q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2)q_per_token_split_into_pairs.shape
句子中在m位置的一对查询向量,旋转角度为m*(rope_theta),其中rope_theta也在模型的配置信息中。
zero_to_one_split_into_64_parts = torch.tensor(range(64))/64zero_to_one_split_into_64_parts
tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250, 0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656, 0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062, 0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469, 0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875, 0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281, 0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688, 0.9844])
freqs = 1.0 / (rope_theta ** zero_to_one_split_into_64_parts)freqs
tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01, 2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01, 8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02, 2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03, 7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03, 2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04, 6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04, 1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05, 5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05, 1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06, 4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06])
freqs_for_each_token = torch.outer(torch.arange(17), freqs)freqs_cis = torch.polar(torch.ones_like(freqs_for_each_token), freqs_for_each_token)
经过以上操作后,我们构建了freq_cis矩阵,存储句子中每个位置的、对查询向量每个值的旋转角度。
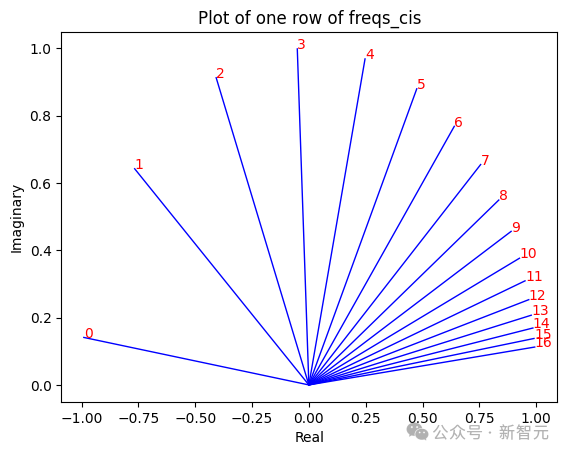
将每对查询向量转换为复数,之后进行与旋转角度进行点积操作。
q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs)q_per_token_as_complex_numbers.shape
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cisq_per_token_as_complex_numbers_rotated.shape
这样我们就得到了旋转后的查询向量,需要再转换回实数形式。
q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers_rotated)q_per_token_split_into_pairs_rotated.shape
q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape)q_per_token_rotated.shape
旋转后的查询向量,维度依旧是 [17x128]。
键向量
键向量的计算与查询向量非常类似,也需要进行旋转位置编码,只是维度有所差异。
键的权重数量仅为查询的1/4,因为需要减少模型计算量,每个权重值被4个注意力头共享。
k_layer0 = model["layers.0.attention.wk.weight"]k_layer0 = k_layer0.view(n_kv_heads, k_layer0.shape[0] // n_kv_heads, dim)k_layer0.shape
torch.Size([8, 128, 4096])
因此这里第一个维度的值为8,而不是我们在查询权重中看到的32。
k_layer0_head0 = k_layer0[0]k_per_token = torch.matmul(token_embeddings, k_layer0_head0.T)k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2)k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs)k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis)k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape)k_per_token_rotated.shape
照着前面查询向量部分的计算流程,就可以得到句子中每个token的键向量了。
查询和键相乘
对句子进行「自注意力」的过程,就是将查询向量和键向量相乘,得到的QK矩阵中的每个值描述了对应位置token查询值和键值的相关程度。
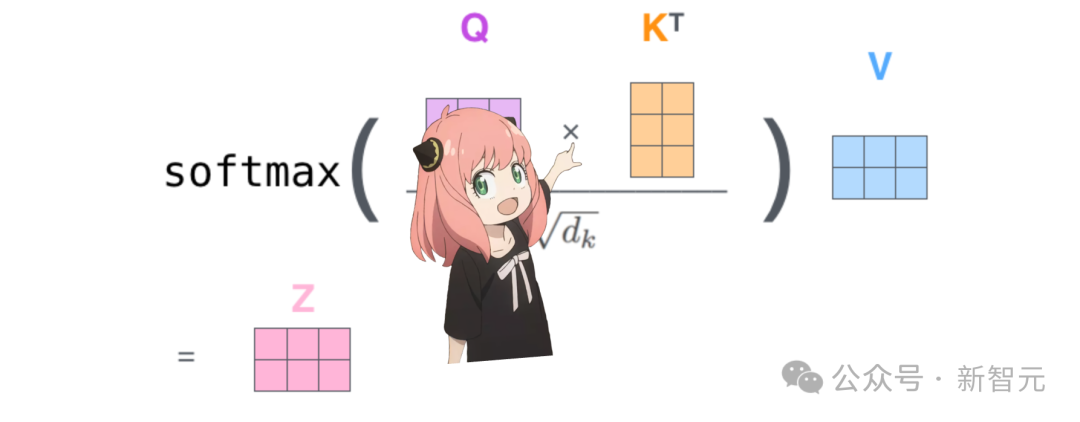
相乘后,我们会得到一个维度为[17x17]自注意力矩阵。
qk_per_token = torch.matmul(q_per_token_rotated, k_per_token_rotated.T)/(head_dim)**0.5qk_per_token.shape
掩码
语言模型的学习目标,是根据句子之前的内容预测下一个token,因此训练和推理时需要将token位置之后的QK分数屏蔽。
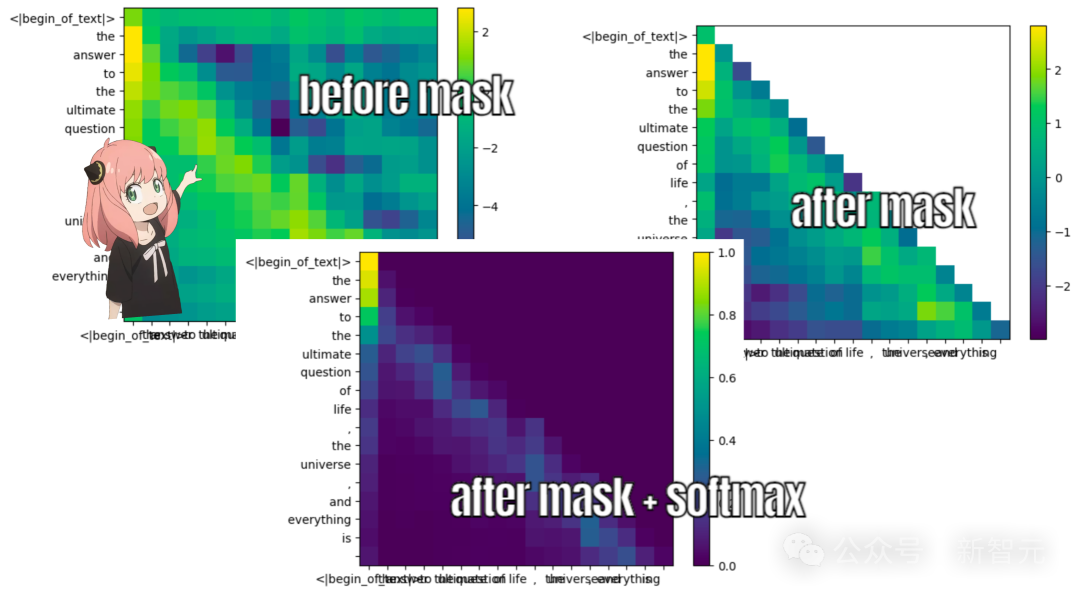
值向量
值权重数量和键权重一样,都是在4个注意力头之间共享(以节省计算量)。
v_layer0 = model["layers.0.attention.wv.weight"]v_layer0 = v_layer0.view(n_kv_heads, v_layer0.shape[0] // n_kv_heads, dim)v_layer0.shape
torch.Size([8, 128, 4096])
之后我们获取第一层第一个注意力头的值权重,与句子embedding相乘,获取值向量。
v_layer0_head0 = v_layer0[0]v_per_token = torch.matmul(token_embeddings, v_layer0_head0.T)v_per_token.shape
注意力向量

将进行过掩码的QK矩阵和句子的值向量相乘,就得到了注意力矩阵,维度为[17x128]。
qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token)qkv_attention.shape
多头注意力
以上得到的注意力矩阵,是第一层第一个注意力头的计算结果。
接下来需要运行一个循环,对第一层中所有32个注意力头进行上述运算过程。
qkv_attention_store = []
for head in range(n_heads): q_layer0_head = q_layer0[head] k_layer0_head = k_layer0[head//4] # key weights are shared across 4 heads v_layer0_head = v_layer0[head//4] # value weights are shared across 4 heads q_per_token = torch.matmul(token_embeddings, q_layer0_head.T) k_per_token = torch.matmul(token_embeddings, k_layer0_head.T) v_per_token = torch.matmul(token_embeddings, v_layer0_head.T)
q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2) q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs) q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers * freqs_cis[:len(tokens)]) q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape)
k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2) k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs) k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis[:len(tokens)]) k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape)
qk_per_token = torch.matmul(q_per_token_rotated, k_per_token_rotated.T)/(128)**0.5 mask = torch.full((len(tokens), len(tokens)), float("-inf"), device=tokens.device) mask = torch.triu(mask, diagonal=1) qk_per_token_after_masking = qk_per_token + mask qk_per_token_after_masking_after_softmax = torch.nn.functional.softmax(qk_per_token_after_masking, dim=1).to(torch.bfloat16) qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token) qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token) qkv_attention_store.append(qkv_attention)
len(qkv_attention_store)
为了并行计算的方便,我们需要把上面展开的矩阵压缩回去。
也就是将32个维度为[17x128]的注意力矩阵,压缩成一个维度为[17x4096]的大矩阵。
stacked_qkv_attention = torch.cat(qkv_attention_store, dim=-1)stacked_qkv_attention.shape
最后,别忘了乘以输出权重矩阵。
w_layer0 = model["layers.0.attention.wo.weight"]w_layer0.shape# torch.Size([4096, 4096])embedding_delta = torch.matmul(stacked_qkv_attention, w_layer0.T)embedding_delta.shape
至此,注意力模块的计算就结束了。
相加与归一化
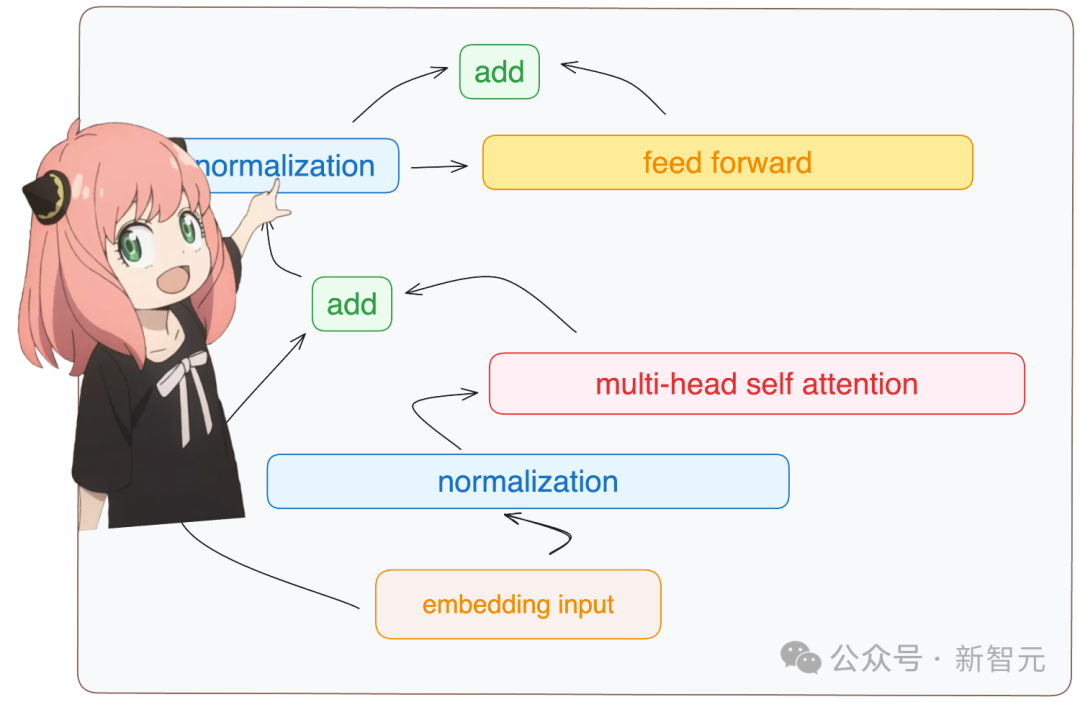
对照这张Transformer层的架构图,在多头自注意力模块之后还需要完成一些运算。
首先将注意力模块的输出与原始的embedding相加。
embedding_after_edit = token_embeddings_unnormalized + embedding_deltaembedding_after_edit.shape
之后进行RMS归一化。
embedding_after_edit_normalized = rms_norm(embedding_after_edit, model["layers.0.ffn_norm.weight"])embedding_after_edit_normalized.shape
前馈神经网络层
Llama 3的Transformer层中使用了SwiGLU前馈网络,这种架构非常擅长在必要情况下为模型添加非线性,这也是当今LLM中的常见操作。
SwiGLU与Vanilla两种前馈神经网络架构的对比于是我们从模型中加载前馈网络的权重,并按照公式计算:
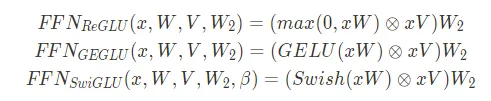
w1 = model["layers.0.feed_forward.w1.weight"]w2 = model["layers.0.feed_forward.w2.weight"]w3 = model["layers.0.feed_forward.w3.weight"]output_after_feedforward = torch.matmul(torch.functional.F.silu(torch.matmul(embedding_after_edit_normalized, w1.T)) * torch.matmul(embedding_after_edit_normalized, w3.T), w2.T)output_after_feedforward.shape
别忘了前馈层之后还有一次相加。
layer_0_embedding = embedding_after_edit+output_after_feedforwardlayer_0_embedding.shape
以上就是一个完整Transformer层的实现,最终输出的向量维度为[17x4096],相当于为句子中每个token重新计算了一个长度为4096的embedding向量。
之后的每一个Transformer层都会编码出越来越复杂的查询,直到最后一层的输出的embedding可以预测句子下一个token。
因此需要再嵌套一个外层循环,将Transformer层的流程重复32次。
final_embedding =
token_embeddings_unnormalizedfor layer in range(n_layers): qkv_attention_store = [] layer_embedding_norm = rms_norm(final_embedding, model[f"layers.{layer}.attention_norm.weight"]) q_layer = model[f"layers.{layer}.attention.wq.weight"] q_layer = q_layer.view(n_heads, q_layer.shape[0] // n_heads, dim) k_layer = model[f"layers.{layer}.attention.wk.weight"] k_layer = k_layer.view(n_kv_heads, k_layer.shape[0] // n_kv_heads, dim) v_layer = model[f"layers.{layer}.attention.wv.weight"] v_layer = v_layer.view(n_kv_heads, v_layer.shape[0] // n_kv_heads, dim) w_layer = model[f"layers.{layer}.attention.wo.weight"] for head in range(n_heads): q_layer_head = q_layer[head] k_layer_head = k_layer[head//4] v_layer_head = v_layer[head//4] q_per_token = torch.matmul(layer_embedding_norm, q_layer_head.T) k_per_token = torch.matmul(layer_embedding_norm, k_layer_head.T) v_per_token = torch.matmul(layer_embedding_norm, v_layer_head.T) q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2) q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs) q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers * freqs_cis) q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape) k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2) k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs) k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis) k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape) qk_per_token = torch.matmul(q_per_token_rotated, k_per_token_rotated.T)/(128)**0.5 mask = torch.full((len(token_embeddings_unnormalized), len(token_embeddings_unnormalized)), float("-inf")) mask = torch.triu(mask, diagonal=1) qk_per_token_after_masking = qk_per_token + mask qk_per_token_after_masking_after_softmax = torch.nn.functional.softmax(qk_per_token_after_masking, dim=1).to(torch.bfloat16) qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token) qkv_attention_store.append(qkv_attention)
stacked_qkv_attention = torch.cat(qkv_attention_store, dim=-1) w_layer = model[f"layers.{layer}.attention.wo.weight"] embedding_delta = torch.matmul(stacked_qkv_attention, w_layer.T) embedding_after_edit = final_embedding + embedding_delta embedding_after_edit_normalized = rms_norm(embedding_after_edit, model[f"layers.{layer}.ffn_norm.weight"]) w1 = model[f"layers.{layer}.feed_forward.w1.weight"] w2 = model[f"layers.{layer}.feed_forward.w2.weight"] w3 = model[f"layers.{layer}.feed_forward.w3.weight"] output_after_feedforward = torch.matmul(torch.functional.F.silu(torch.matmul(embedding_after_edit_normalized, w1.T)) * torch.matmul(embedding_after_edit_normalized, w3.T), w2.T) final_embedding = embedding_after_edit+output_after_feedforward
最后一个Transformer层的输出维度与第一层相同,依旧是[17x4096]。
final_embedding = rms_norm(final_embedding, model["norm.weight"])final_embedding.shape
此时需要利用输出解码器,将最后一层输出的embedding先进行归一化处理,再转换为token。
final_embedding = rms_norm(final_embedding, model["norm.weight"])final_embedding.shape# torch.Size([17, 4096])
model["output.weight"].shape# torch.Size([128256, 4096])
logits = torch.matmul(final_embedding[-1], model["output.weight"].T)logits.shape
输出的向量维度与分词器中词汇数量相同,每个值代表了下一个token的预测概率。
模型预测下一个词是42?
和《银河系漫游指南》的梦幻联动(不知道是不是作者故意设置成这样的)
next_token = torch.argmax(logits, dim=-1)next_token
tokenizer.decode([next_token.item()])
至此,我们就完成了Llama 3对输入句子进行下一个token预测的全过程。
https://github.com/naklecha/llama3-from-scratch