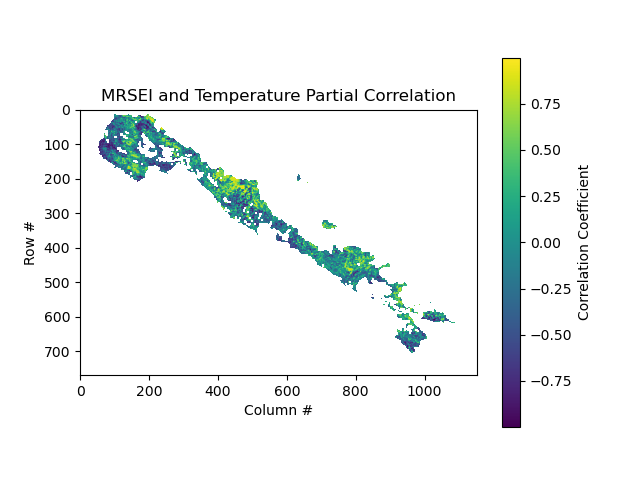
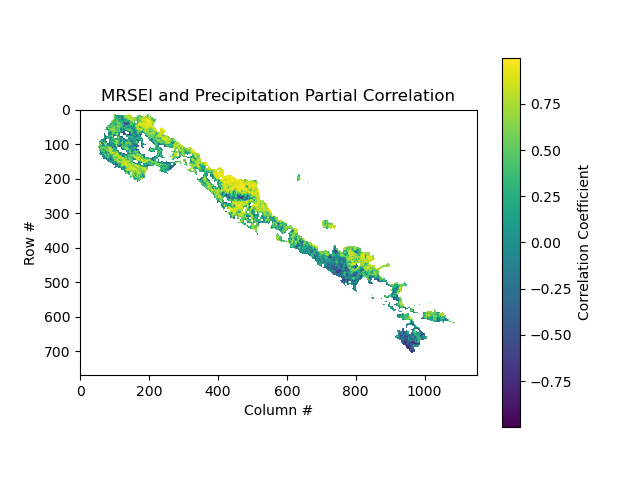
逐像元偏相关性分析是一种空间数据分析技术,用于测量栅格数据集中各像素点上两个或多个变量之间的相关性,同时控制其他变量的影响。这种方法允许研究者识别并量化在特定地理位置的环境变量之间的直接关系。
在本案例中我使用,MRSEI(变量a)与降水(变量b)、温度 (变量c)、和HFP(变量d)之间的偏相关系数分析。
理解偏相关
首先,需要理解偏相关(partial correlation)的概念。偏相关是衡量两个变量之间关系的统计方法,同时控制其他一个或多个变量的影响。基本思想是,当你想了解变量A和变量B之间的真实关系时,需要排除变量C、D等其他变量的干扰。
逐像元分析
在遥感数据分析中,每个像素(pixel)都可以被视为一个观测点。逐像元分析意味着对每个像素分别进行分析,而不是将整个图像作为一个整体来分析。
统计模型
在实际操作中,通常使用线性回归模型来计算这些关系。首先,使用控制变量对感兴趣的变量(例如,MRSEI和降水)进行回归,以得到残差(residuals)。然后,计算这些残差之间的相关系数,这个相关系数即为偏相关系数。
偏相关系数的计算:
首先,对于每个像素,使用线性回归模型独立地估计感兴趣的变量(比如X和Y)对控制变量(比如Z)的影响。这可以通过下面的回归方程实现:
Y = β₀ᵞ + β₁ᵞZ + εᵞ
X = β₀ˣ + β₁ˣZ + εˣ
从上述模型中得到的残差( εᵞ和εˣ)代表了在控制Z变量后Y和X的变化。
使用以下公式计算偏相关系数:
其中,Cov(εˣ, εᵞ) 表示残差之间的协方差,Var(εˣ) 和 Var(εᵞ) 分别表示X和Y残差的方差。
解释结果
偏相关系数rᵧˣ⋅𝘡 表示在控制其他变量(如Z)的影响后,X和Y之间的相关程度。偏相关系数的范围通常在-1到1之间,其中1表示完全正相关,-1表示完全负相关,0表示没有相关性。
最终得到的偏相关系数可以告诉我们,在控制了其他变量的影响之后,两个感兴趣的变量之间的关联程度。这是一种剔除了可能的混杂因素影响后的“纯净”关系。
使用python多线程逐像元偏相关性分析
我的文件结构如图所示标红的为用到的代码,其他的皆为测试代码,我使用了多线程来加快运行,[770,1150]的矩阵这样计算,16G的mac m2为15分钟,比不用多线程快了6倍。
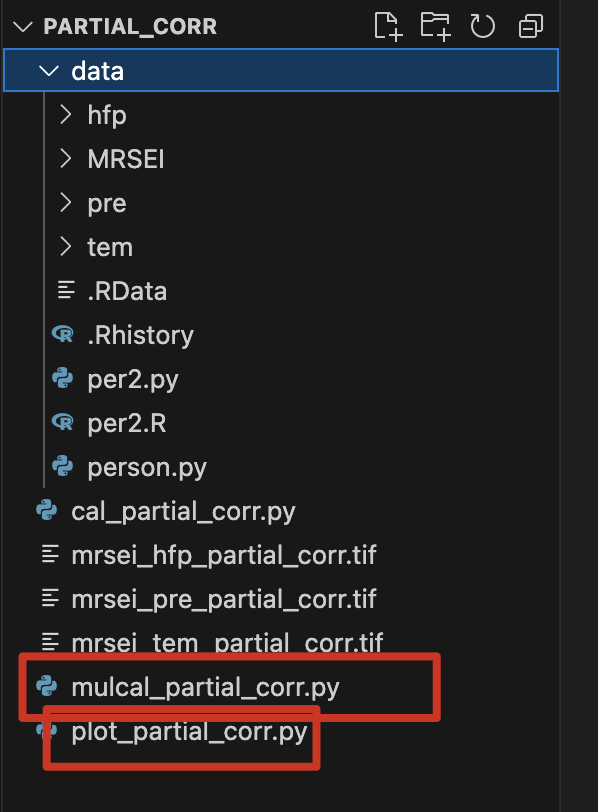
首先引入包和去除烦人的提醒
import rasterioimport numpy as npfrom sklearn.linear_model import LinearRegressionfrom multiprocessing import Poolimport itertoolsimport numpy as np
np.seterr(divide='ignore', invalid='ignore')
定义读取栅格数据的函数:
def read_raster(file_path): with rasterio.open(file_path) as src: return src.read(1), src.meta
定义计算偏相关系数的函数,计算两个变量(x和y)在控制其他变量的情况下的偏相关系数。这是通过线性回归模型计算残差并使用它们的相关系数来完成的。
def calculate_partial_correlation(x, y, controls): if np.isnan(x).any() or np.isnan(y).any() or np.isnan(controls).any(): return np.nan model = LinearRegression().fit(controls, y) residuals_y = y - model.predict(controls) model = LinearRegression().fit(controls, x) residuals_x = x - model.predict(controls) return np.corrcoef(residuals_x, residuals_y)[0, 1]
worker函数为多进程池设计,用于处理每个像素的计算。它接受像素数据(包括特定像素的MRSEI, PRE, TEM, 和 HFP值),计算MRSEI与PRE、TEM、HFP的偏相关系数,并返回结果及其像素位置。
def worker(pixel_data): i, j, data = pixel_data x_mrsei = data['mrsei'] y_pre = data['pre'] y_tem = data['tem'] y_hfp = data['hfp'] controls_pre = np.column_stack([y_tem, y_hfp]) controls_tem = np.column_stack([y_pre, y_hfp]) controls_hfp = np.column_stack([y_pre, y_tem]) pre_corr = calculate_partial_correlation(x_mrsei, y_pre, controls_pre) tem_corr = calculate_partial_correlation(x_mrsei, y_tem, controls_tem) hfp_corr = calculate_partial_correlation(x_mrsei, y_hfp, controls_hfp) return (i, j, pre_corr, tem_corr, hfp_corr)
主函数,我写注释了
def main(): years = range(2000, 2006)
file_paths = {var: [f'data/{var}/{year}.tif' for year in years] for var in ['tem', 'pre', 'hfp', 'mrsei']} rasters = {var: np.array([read_raster(fp)[0] for fp in fps]) for var, fps in file_paths.items()}
min_shape = tuple(min(sizes) for sizes in zip(*(r.shape for r in rasters['mrsei'])))
pixel_data = [(i, j, {k: v[:, i, j] for k, v in rasters.items()}) for i, j in itertools.product(range(min_shape[0]), range(min_shape[1]))] partial_corrs = { 'mrsei_pre': np.full(min_shape, np.nan), 'mrsei_tem': np.full(min_shape, np.nan), 'mrsei_hfp': np.full(min_shape, np.nan) }
pixel_data = [(i, j, { 'mrsei': rasters['mrsei'][:, i, j], 'pre': rasters['pre'][:, i, j], 'tem': rasters['tem'][:, i, j], 'hfp': rasters['hfp'][:, i, j] }) for i, j in itertools.product(range(min_shape[0]), range(min_shape[1]))]
with Pool() as pool: for idx, result in enumerate(pool.imap(worker, pixel_data), 1): i, j, pre_corr, tem_corr, hfp_corr = result partial_corrs['mrsei_pre'][i, j] = pre_corr partial_corrs['mrsei_tem'][i, j] = tem_corr partial_corrs['mrsei_hfp'][i, j] = hfp_corr
if idx % 1000 == 0: print(f'Processed {idx} pixels')
_, meta = read_raster(file_paths['mrsei'][0])
meta['dtype'] = 'float32' meta['count'] = 1 for var in ['mrsei_pre', 'mrsei_tem', 'mrsei_hfp']: with rasterio.open(f'{var}_partial_corr.tif', 'w', **meta) as dst: dst.write(partial_corrs[var].astype('float32'), 1)
if __name__ == '__main__': main()
运行时如图所示
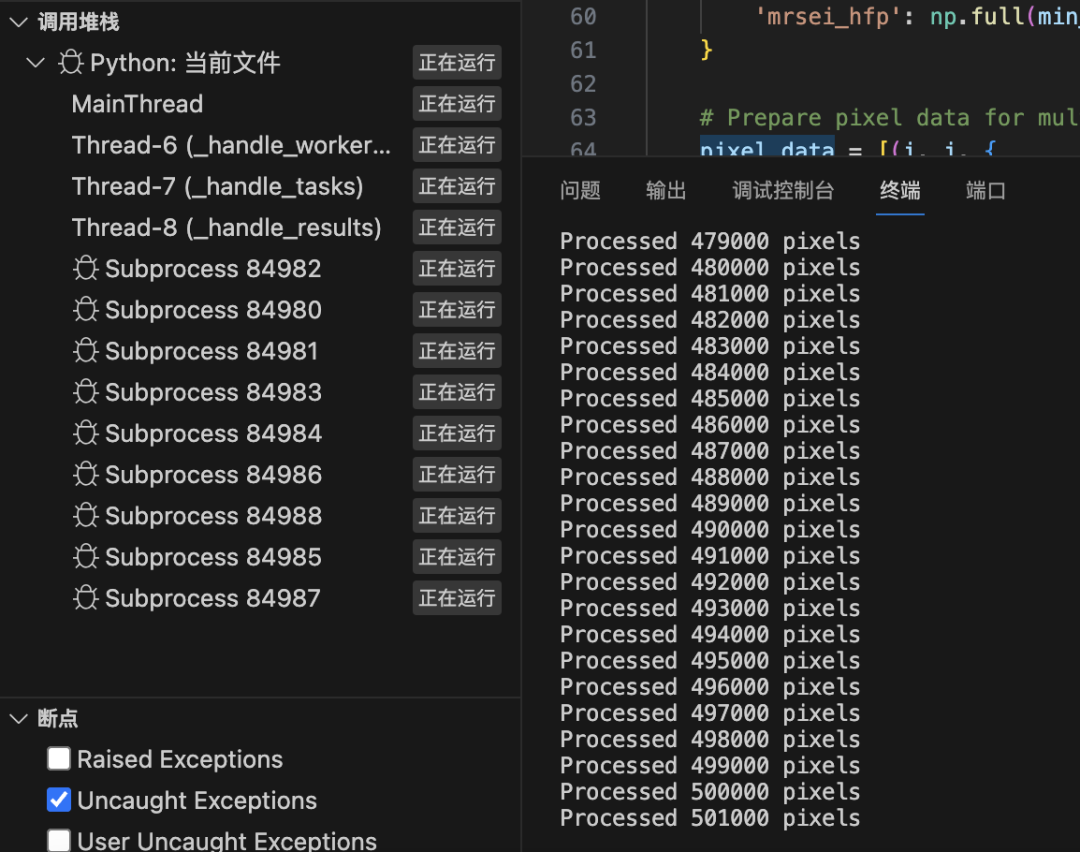
结果绘图
import matplotlib.pyplot as pltimport rasterioimport numpy as np
def plot_raster(file_path, title): with
rasterio.open(file_path) as src: raster = src.read(1) raster[raster == src.nodata] = np.nan
plt.imshow(raster, cmap='viridis') plt.colorbar(label='Correlation Coefficient') plt.title(title) plt.xlabel('Column #') plt.ylabel('Row #') plt.show()
plot_raster('mrsei_pre_partial_corr.tif', 'MRSEI and Precipitation Partial Correlation')plot_raster('mrsei_tem_partial_corr.tif', 'MRSEI and Temperature Partial Correlation')plot_raster('mrsei_hfp_partial_corr.tif', 'MRSEI and HFP Partial Correlation')