
会计舞弊是一个世界性的难题。如果不及时发现和防范,不仅会对欺诈企业的利益相关者造成重大损害,也会间接对众多非欺诈企业的利益相关者造成重大损害。遗憾的是,会计舞弊很难被发现,此外,即使检测到会计舞弊,其实际上已经造成了破坏性。因此,高效和有效的企业会计欺诈检测方法将为监管者、审计师和投资者提供重要价值。
为开发出一种基于数据驱动的、高效的企业会计舞弊行为检测方法,来自上海交通大学的鲍杨、新加坡国立大学的柯滨、武汉大学的李斌、弗吉尼亚大学的Y. Julia Yu以及南洋理工大学的张杰于2020年3月在会计学国际顶级期刊《Journal of Accounting Research》发表论文“Detecting Accounting Fraud in Publicly Traded U.S. Firms Using a Machine Learning Approach”。
文章使用机器学习方法开发了一个最先进的欺诈预测模型。另外,文章展示了在模型构建中结合领域知识和机器学习方法的价值。通过使用最强大的机器学习方法之一——集成学习,结合会计数据,文章表明所提出的新的欺诈预测模型比现有的基准模型有很大的优势。
相关阅读:
机器学习在经管领域的应用有哪些经典论文?
经济研究与机器学习,国际顶刊发表的29篇经典论文
本文的研究目标是利用公开交易的美国企业的财务报表数据,在样本外开发一个新的会计舞弊预测模型。作者使用美国证券交易委员会( SEC )的会计和审计执行报告( AAERs )中披露的重大会计错报作为会计舞弊样本。尽管存在有用的会计舞弊非财务预测指标(例如,高管的个人行为),但文章仅使用可获得的财务数据(公开会计财务数据),原因有二。首先,基于公开可用的财务数据的欺诈预测模型可以低成本地应用于任何上市公司。第二,现有会计文献中的舞弊预测模型大多也依赖于公开可得的财务数据。通过将预测因子仅限于财务数据,文章所提出的欺诈预测模型的性能可以与此类现有模型的性能进行比较。
文章使用的样本涵盖了1991 - 2008年期间所有公开上市的美国企业。作者所有的欺诈预测模型都需要一个训练集和一个测试集。为保证模型训练的可靠性,作者要求训练集应当超过10年。此外,作者进一步要求最后一个测试集年的财务结果公告与测试集的财务数据公开时间有24个月的差距。这样做是因为,欺诈的初始披露平均需要大约24个月。因此,文章使用样本2003 - 2008的最后六年作为测试期间,并且安排了滚动窗口训练与测试。例如,“训练集为1991 - 2001年、测试集为2003年”或“1991 - 2003年为训练集、2005年为测试集”。
集成学习是机器学习的一个主要范式,最近在许多实际应用中取得了显著的成功。与传统的机器学习方法(例如, SVM方法)通常生成单个估计器不同,集成学习方法将一组基估计器(例如,决策树)的预测结合起来,以提高泛化能力和稳健性。先前的研究表明,集成通常优于任何单个估计。然而,由于可能存在类别不平衡问题,传统的集成学习方法通常需要结合平衡训练数据类别分布的采样技术。
在文章中,作者采用了一种称为RUS-Boost的集成学习的变体。RUS-Boost试图同时利用高效的欠采样技术和当前最有影响力的集成算法AdaBoost。研究发现,RUS-Boost由于其简单性,即表现出高性能,而且在计算效率上也存在相当的优越性。
评估分类模型样本外性能的常用方法是执行n折交叉验证。由于文章所考虑的欺诈数据本质上是跨期的,执行标准的n折交叉验证是不合适的。因此,如前所述,作者将样本期(即2003 - 08年)的最后几年作为测试期,所有较早的年份作为训练集。并且在训练集上计算两个重要的表现指标:AUC与NDCG@K,作为模型的样本外表现测度。
其中AUC(Area Under Curve)是曲线下面积的英文缩写,这里的曲线通常指的是ROC曲线(受试者工作特征曲线)。AUC作为一个评价指标,常用于二分类模型的评价。机器学习中的很多模型对于分类问题的预测结果大多是概率,即属于某个类别的概率。计算AUC时,需要首先设定一个阈值,将概率转化为类别。然后计算每个阈值下的“真正例率”(True Positive Rate)和“假正例率”(False Positive Rate),分别以它们为纵轴和横轴画出ROC曲线,ROC曲线下的面积即为AUC的值。AUC的值介于0.5和1之间,其中0.5表示分类器等同于随机猜测,而1表示分类器完美。因此,AUC越接近1,说明分类器的性能越好。而欺诈预测任务也可以被认为是一个排序问题。具体来说,可以仅对那些被预测具有最高舞弊可能的样本进行模型表现评价。在这种场景下,欺诈预测模型的性能可以通过排序问题中常用的性能评价指标NDCG @ k来衡量。
在具体的对比模型表现中,为了更清楚地看到将原始数据与集成学习结合的价值,作者将分解为三个步骤开展。首先,通过继续使用逻辑回归,但将模型输入从14个财务比率改为28个原始财务数据项来检验预测性能的改进。其次,通过使用28个原始数据项和集成学习方法来检验作者提出的模型的欺诈预测性能。第三,通过使用集成学习方法,但将模型输入从28个原始数据项改为14个财务比率或14个财务比率和28个原始数据项的组合来检查欺诈预测性能。
下表显示了基于28个原始财务数据项的逻辑回归模型的预测性能。基于28个原始金融数据项的逻辑回归模型的平均AUC为0.690,高于现存文献中的平均AUC。然而,基于28个原始数据项的逻辑回归的NDCG @ k的平均值仅为0.006,低于现存文献的平均值。总的来说,结果并没有证实或反对传统预测方法加上原始会计数据能否提升预测舞弊效力。
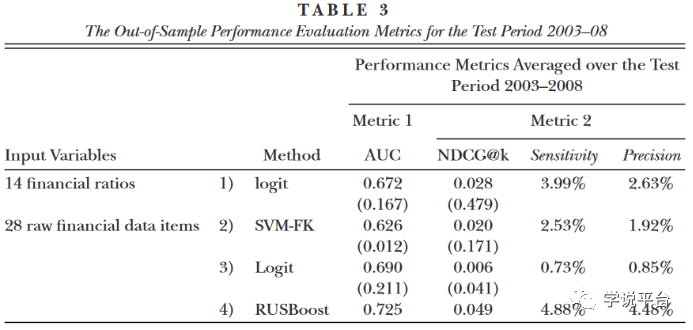
使用相同的28个原始会计数据,接下来文章考察是否有可能通过使用更先进的数据挖掘方法——集成学习来提高样本外欺诈预测性能。尽管每个算法都有一些需要微调的参数,但值得注意的是,AdaBoost (以及RUSBoost等变体)被认为是最好的样本外分类算法之一,因为它在没有仔细调参的情况下仍然表现良好。前表(Table3)报告了基于2003 - 2008年测试期间的原始财务数据的集成学习模型的样本外性能。集成学习方法的平均AUC为0.725,远大于现存文献中平均AUC ( 0.672 )。使用NDCG @ k作为替代评估标准,作者发现集成学习方法的NDCG @ k平均值为0.049,大于同样大于现存文献NDCG @ k平均值。为了更好地评估各种预测模型在2003 - 2008年测试期间的差异表现的经济意义,文章还计算了使用NDCG @ k方法识别的真实欺诈观察数,其中k = 1 % (见原论文在线附录表A2)。文章发现,集成学习模型,在测试期间2003 - 2008年共识别了16个欺诈案例。相比之下,现存文献的模型的仅识别了7-9个。这些结果表明,集成学习模型相对于两个基准模型的性能差异在经济上也是显著的。
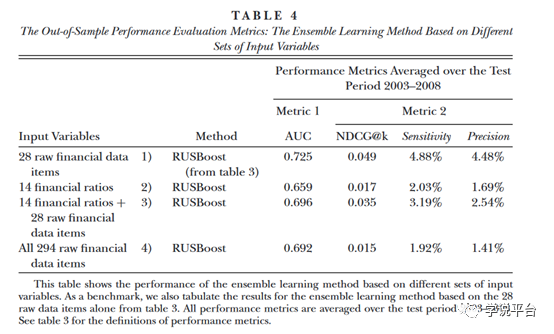
在这一部分中,作者进一步研究了单独使用14个比率,或者同时使用28个原始数据项和14个比率,是否可以提高集成学习方法的性能。表4报告了这两种替代模型的样本外性能统计。作者没有发现两个备选集成学习模型优于单独基于28个原始数据项的集成学习模型的证据。这一证据与文章的猜想是一致的,一旦考虑了28个原始数据项,再加上一个灵活而强大的机器学习方法,算法能够自动组合指标,并且获得更好的效果。
作者使用机器学习方法开发了一个先进的欺诈预测模型,同时展示了在模型构建中结合领域知识和机器学习方法的价值。具体的,文章从两个方向改善了现存文献。首先,根据现有的会计理论选择,作者选择模型输入,但与以前的会计研究不同的是,文章仅使用原始会计数字而不是财务比率。另外,在模型上,作者还使用了强大的机器学习方法之一,集成学习方法。
为了评估欺诈预测模型的性能,作者引入了一种新的常用于排序问题的性能评价指标,该指标更适合欺诈预测任务。结果表明文章所提出的新的欺诈预测模型比两个基准模型有很大的优势,既提升了模型的预测效果,还改善了模型的经济效应。