我们中的许多人在以"少就是多原则"为基础的传统中构建了的计量经济学相关的框架。在一些计量经济学教科书的导言中,“少就是多原则”被作为“模型构建中的基本思想”的第一条提出:即“在实践中,重要的是我们使用尽可能少的参数来进行经济模型的表示”。
而这一简约的原则似乎与现代机器学习算法所采用的大规模参数化发展发生冲突。领先的GPT-3语言模型使用了1750亿个参数,而更为先进的GPT-4模型更是在120层结构中有1.8万亿个参数。即使是现存关于股票收益率的预测模型中比较简单的神经网络也有大约30000个参数。对于一个比较传统的计量经济学家来说,如此丰富的参数化令人望而生畏,容易出现过拟合,并且可能会对样本外的模型性能造成灾难性的影响。
实际上,在各种非金融领域的研究结果表示,复杂模型明显优于简约模型。在计算机视觉和自然语言处理等应用中,带有大规模参数化的模型,以及恰好拟合训练数据的模型,往往是样本外表现最好的模型。在评估神经网络文献的状态时, “似乎你能得到的最大网络结构就是你能找到的最优模型”。显而易见,现代机器学习已经将简约原则推到了风口浪尖。
我们正在寻找一个理论基础来解释这一庞大参数化的成功,并简洁地回答如下问题:“为什么重度参数化的神经网络不会过度拟合数据而导致性能衰减?”在这一部分作者提供了一个可能的思路与解答。
Kelly et al.(2022a)提出了一个思想实验。设想一个分析师寻求一个成功的收益预测模型。假设资产收益R潜在的真实生成模型为:
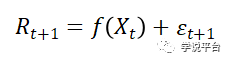
其中预测变量X的集合可能是分析师已知的,但真实的预测函数f是未知的(分析师有可能获取所有收益率相关信息,但绝对不可能知道这些信息真实组合关系)。在不了解f的情况下,分析师决定用一个基本的神经网络来逼近f:
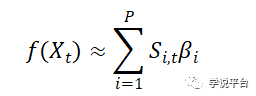
该回归中的每个特征S都是原始预测变量的一个非线性变换,即:
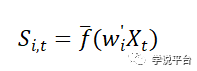
最后,分析师估计收益率对非线性变化后得特征S进行模型参数估计:
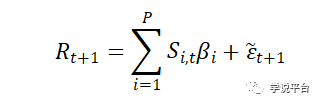
假设,分析师有T个训练观测值可供使用,所以他必须选择一个合适的模型复杂度,在上面的例子中,就是模型的参数数量P。P较小的简单模型获得的参数方差较低,但P较大的复杂模型(甚至P > T)能更好地逼近真实收益率。那么分析师应该选择何种水平的模型复杂度呢?
令人惊讶的是,Kelly et al . ( 2022a )表明分析师应该使用她所能计算的最大规模模型!为了得出这个答案,Kelly et al . ( 2022a )使用了两个关键的数学工具来分析复杂的机器学习模型。1.具有生成非线性特征的岭回归和2.随机矩阵理论,用于分析当P相对于训练数据观测值的数量很大时的估计量行为。
1.带有生成变量的岭回归
构建岭回归的第一个假设,是根据
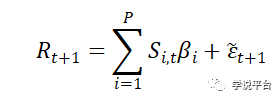
提出的高维线性预测模型,我们称之为"经验模型"。对与这一式子的解释并不是资产收益受制于大量的线性基本面驱动力。相反,DGP(数据生成过程)是未知的,但可以用一些潜在驱动变量X的非线性变换S来近似。在机器学习的语言中,S是由原始特征X衍生出来的“生成特征”,例如X的一个非线性变化S=X²。
由逼近理论可知,如果我们真的希望通过S以线性方式逼近收益率背后真实的DGP,则需要一个无穷级数展开式(P为无穷大),但在实际中我们却被有限的P所限制。机器学习的一个基本前提是可以利用灵活(大P )的模型规格来改进预测。它们的估计可能是有噪声的(高方差),但提供了更精确的近似或预测(小偏差)。
构建岭回归的第二步,是推导上述岭回归估计量的显式公式:
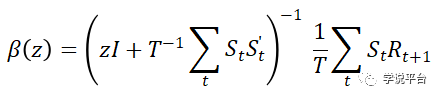
式中,z为收缩参数,是分析的关键。
最后,为了刻画高复杂度模型给投资者带来的经济后果,Kelly et al . ( 2022a )假设投资者利用预测结果构建了交易策略:
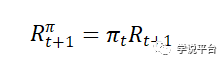
其中,Π为投资权重,将风险资产头寸按模型的收益预测进行调整。对于他们的分析,设定Π等于他们的复杂预测模型的样本外预期收益。并且他们假设投资者幸福感是Sharpe比率来衡量:
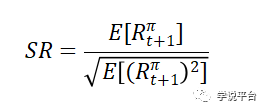
2.随机矩阵理论
上面提到的机器学习模型的岭回归公式就像神经网络中的线性回归公式。分析的重点就在于,给定上面的模型、显式公式、投资者效用后,我们可以对复杂模型(在P→∞或P/T→c>0)的样本外性能进行一些讨论。机器学习的必要渐近性不同于标准计量方法中的大样本渐进 (在P固定的情况下,对T→∞使用渐近逼近)。随机矩阵理论非常适合描述岭回归在大P设定下的行为。为了简化记号,我们将T从讨论中剔除,即假设分析师始终拥有同一时间窗口的数据,简单将比率c=P/T作为模型复杂度的代表。
分析岭回归中参数β行为的关键是信号的样本协方差矩阵
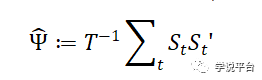
随机矩阵理论可以用于描述 Ψ特征值的极限分布。对这种分布的了解足以确定岭回归的样本外预测性能( R2 ),以及相应的择时策略的样本外夏普比率。更具体地说,这些量是由下式这一Ψ特征值分布的极限Stieltjes变换,决定的(原文注:关于这一点的详细阐述见Kelly et al. ( 2022a )的第3节和第4节):
换句话说,模型复杂度在理解模型行为中起着至关重要的作用。如果T以比预测变量个数(即c→0 )更快的速度增长,传统计量方法下的大T和固定的P渐近理论就会出现。在这种情况下,模型的预期样本外行为与样本内估计的行为是一致的。而当情况考虑为具有稀缺数据的高度参数化的机器学习模型,P/T→c>0时,接下来的分析结果显示模型的预期样本外行为与样本内估计的行为出现极大分歧。
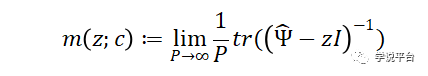
Kelly等人( 2022a )对高复杂度机器学习模型和相关交易策略的性质给出了严格的理论陈述。我们目前的论述主要集中在这些结果的定性方面,其基础是它们对市场回报预测问题的分析。特别地,他们假设总收益波动率等于每年20 %,如果真正的函数形式和所有的信号都能完全提供给分析师时,可预测得R2为每月20 %。但现实中由于没有足够的数据来支持模型的参数化,因此最佳可行的预测R2假设为每月1 %。
在这个分析中,假设真实的未知DGP的复杂度为c = 10。参数q∈[ 0、1 ]决定了实证模型相对于真实模型(DGP)的复杂程度。我们分析了复杂度从非常简单的模型( q≈0 , cq≈0)到高度复杂的(q=1 , cq=10)的模型,复杂度很低的模型是预测能力较差的模型,但其参数可以精确估计。随着cq的增大,实证模型逐步逼近真值,但估计参数的方差增大。
首先考虑普通最小二乘( OLS )估计量 β,它是正则化参数z = 0时的特例。由于这个模型的过度简单化,它并没有能力去拟合真实DGP,其对应R2也就实际上为零。随着P的增大,模型的逼近程度提高,但最小二乘估计的分母变大,预测误差方差迅速增大。这一现象如下图所示,普通最小二乘( OLS )估计量下的模型预测能力对应于下图左侧的Ridgeless曲线,可以看到无论模型纳入多少变量(cq如何变化),模型表现R2始终为0:
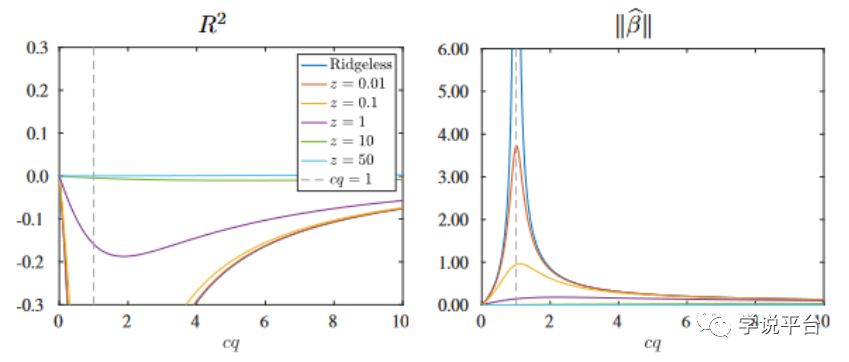
有趣的是,当模型复杂度上升(P超过T, cq超过1),ridgeless回归的R2值上升了。其原因是,随着c变大(模型变量增加),回归有更大的解空间进行搜索,从而可以找到更优的参数解。也就是说,尽管z→0(不进行任何主动的正则化),回归仍然正则化了最小二乘估计量,且c越大这种自动的正则化就越强。而且当c很大时,模型样本外R2会逐渐向正值移动。这一结果对标准的金融经济学理论强调模型简约性的观点提出了挑战,表明可以通过将模型维度远远推到样本容量之外来提高收益预测的准确性。
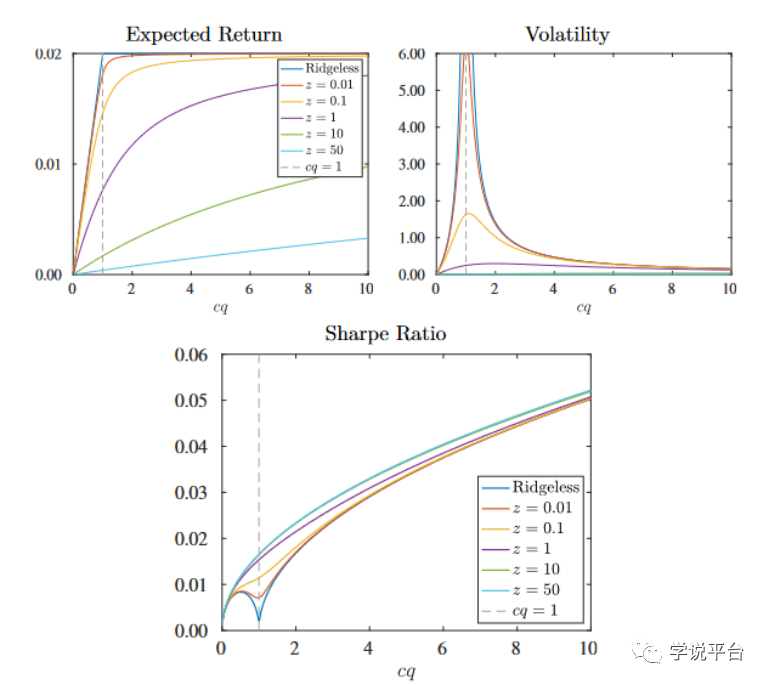
完成对预测效果的分析后,上图则将注意力转向了经济后果分析。上图右右侧显示机器学习交易策略的波动率是模型复杂度的函数。该策略的波动率随着β范数(参数大小)和R2
移动。重要的是,当模型复杂度超过c = 1时,随着模型复杂度的增加,交易策略波动率不断减小。这表示复杂性提高了估计量的隐含收缩率,从而降低了收益波动率。左侧则显示了高复杂度模型的样本外预期收益。可以看刀随着模型复杂度(cq)的提升,模型逐步地逼近DGP,并单调地增加交易策略的预期收益。
这对投资者效用意味着什么?上图中的下侧显示了期望样本外夏普率的效用。我们不妨从夏普比率的定义出发,分别考虑上图左侧与右侧关于收益和方差。1.预期收益纯粹反映了预测偏差。对于低复杂度模型,偏差来自于模型误设(太简单),而不是收缩(正则化)。而对于高复杂度模型,错误指定偏差较小,但收缩偏差变大。但分析表示(上图左侧),预期收益随着复杂性的增加而增加,揭示了当涉及到预期收益时,误设偏差比收缩偏差的成本更高(模型过于简单带来的损失远大于正则化带来的成本)。2.策略的波动率则纯粹是关于预测方差的影响。上图右侧显示无论是简单模型,还是高度复杂模型,均产生较低方差。最终,就导致了样本外夏普率的随着复杂度的增加而增加(上图下侧)。
总之,这些结果挑战了本节开头讨论的计量经济学中的简约教条,证明在现实案例中,复杂性是一种提升预测精度与投资者效用的有力工具。与传统相反,通过推动模型参数大规模化,理论上可以提高机器学习组合的性能。
Didisheim et al. ( 2023 )对Kelly et al. ( 2022a )的分析进行了多种扩展,引入了"复杂性差异",定义为样本内和样本外绩效的期望差异。为了简单起见,考虑一个正确设定的实证模型。在c≈0的低复杂度环境中,大数定律适用,因此样本内估计收敛到真实模型。由于这种收敛性,模型的样本内表现恰恰说明了其预期的样本外表现。也就是说,在没有复杂性的情况下,样本内行为和样本外行为之间不存在任何差异。
但是当c>0时,会出现一个由两个分量组成的复杂性差异。复杂度过度地放大了样本内的可预测性,即产生了样本内的过拟合,也是第一个差异来源。但高度的复杂性也意味着经验模型没有足够的数据(相对于其参数化)来还原真实的模型,这是大数定律因复杂性而失效的表现。这就产生了第二个差异来源,这是相对于真实模型的样本外性能的不足。这种不足可以被认为是由于模型复杂性导致的"学习极限"。而复杂度差异,样本内和样本外性能之间的期望差异,就是过拟合和学习限制同时作用下的结果。
复杂性楔子对资产定价有许多有趣的影响。给定一个已实现的(可行的)预测R2,可以利用随机矩阵理论反推出“真实”(但不可行,因为真实模型和真实信息集我们永远不可能知道)模型的可预测程度。已有多项研究进行了记录使用机器学习模型进行显著为正的样本外收益预测。这一事实,结合对学习极限的理论推导,表明“真实”预测R2必须要高得多。与此相关,即使真实模型隐含着极大的套利机会(或仅仅是很高的Sharpe比率),学习的限制也使得这些对现实世界的投资者来说是无法获得的。在现实的经验设定中,Didisheim et al. ( 2023 )认为,由于无法准确估计复杂的统计关系,可获得的夏普比率相对于真实的数据生成过程衰减了大约一个数量级。
Da et al. ( 2022 )考虑了一个独特的经济环境,在这个环境中,代理人,即套利者,采取统计套利策略,努力最大化他们的样本外夏普比率。这些套利者在学习alpha的DGP时也面临着统计上的障碍(像这里的"复杂性")。Da et al . ( 2022 )的研究表明,无论套利者使用何种机器学习方法,在某些低信噪比环境下都无法实现最优夏普率。此外,即使套利者采取了最优的可行交易策略,他们的夏普比率与最优的不可行比率之间仍然存在很大的差距。在本文的章节4.6中,详细讨论了每篇论文的细节。
文中出现的参考文献:
Da, R., S. Nagel, and D. Xiu. (2022). “The Statistical Limit of Arbitrage”. Tech. rep. Chicago Booth.
Didisheim, A., S. Ke, B. Kelly, and S. Malamud. (2023). “Complexity in Factor Pricing Models”. Tech. rep. Yale University.
Kelly, B., S. Malamud, and K. Zhou. (2022a). “Virtue of Complexity in Return Prediction”. Tech. rep. Yale University.