风电功率预测对间歇性能源并网和消纳具有重要意义。随着风力发电的装机容量不断上升，风资源波动性和随机性带来的影响日益显著，对电网运行和风电消纳带来了新的挑战。对风电场输出功率进行预测是缓解电力系统调峰调频压力，提高风电消纳能力的有效手段之一。
传统风电功率预测方法包括物理法和时间序列法等。近年来，随着深度学习技术的发展，一个常用的预测方法是采用深度学习模型建立气象特征和风电功率间的映射关系。一些学者通过提出基于深度置信网络和回声状态神经网络等深度神经网络的风电功率预测模型，降低了功率预测误差。
除了功率预测外，深度神经网络也被广泛应用于其他领域的预测问题。例如，用于负荷预测、交通预测等的LSTM，进行光谱分析和人类动作识别的双向长短时记忆神经网络（Bidirectional LSTM neural network, BLSTM）， 图像信号处理采用的CNN，以及基于堆叠降噪自编码器（stacked denoised autoencoder, SDAE）的动作和文本识别方法等。
与传统浅层人工神经网络相比，深度学习对海量数据具有更强大的学习和泛化能力。目前的深度学习模型种类众多，不同模型有着各自的适用场景。例如，CNN侧重于挖掘网格数据的空间关联性，LSTM和BLSTM则侧重于挖掘序列信息的时间关联性。
对于具有强波动性的风电而言，位于不同地理位置的风电场，其各自的最优预测模型很难做到统一；同时，也很难有一个固定的预测模型能在一年四季不同气象状况下均能保持最优。因此 , 可以采用多种深度学习预测模型组合的方式，提升短期风电功率预测精度。
本文提出基于多参数风过程匹配与深度学习模型自适应选择的短期风电功率预测方法，首先通过多参数组合匹配法从历史样本库中为待预测样本匹配相似度最高的历史样本；再评价不同深度学习模型对该历史最相似样本的适用性，并选取最适合的模型对待预测样本进行功率预测；最后通过算例验证了所提方法的有效性。
1 基于多参数风过程匹配与深度学习模型
自适应选择的短期风电功率预测
1.1 总体框架
图1所示为本文提出的基于多参数风过程匹配与深度学习模型自适应选择的风电短期功率预测模型。该模型分为基于多参数组合匹配法的历史相似风过程匹配，以及基于深度学习模型自适应选择的短期功率预测两个阶段，包含4个步骤。
步骤1 参数构造。将空间风资源等效为用以量化其特性的参数，包含相关性、距离、极差、方差和均值。
步骤2 历史风过程匹配。采用多参数组合匹配法，为每段待预测风过程在历史样本库中匹配相似度最高的历史风过程，记为历史最相似样本。
步骤3 模型适用性评估。采用历史最相似样本评价各深度学习模型的适用性。
步骤4 最适模型功率预测。依据历史最相似样本的模型适用性评价结果，选取适用性最高的深度学习模型对待预测样本进行功率预测。
图1 多参数风过程匹配与模型自适应选择的总体框架图
1.2 基于多参数组合匹配法的历史相似风过程匹配
多参数组合匹配法的示意图如图2所示，该方法分为参数构造和相似度匹配两个步骤。
1.2.1 参数构造
为便于样本间的对比匹配，采用5个参数对预测样本的风资源进行定量描述，分别是相关性、距离、极差、方差和均值。
（1）相关性r
相关性用于反映风过程随时间的增减趋势。灰色相似度通过测量变化的趋势，能有效反映序列数据的走向趋势。本文采用灰色相似度反映趋势相关性。
记待预测样本为 x0、历史样本库中的第i个历史样本为 xi，则 x0 和 xi 在第j个特征分量的相关性为
式中，Δi (j)=v0(j)-vi(j)；ρ是辨识系数，取值为0.5。本文采用的风资源包含10、30、100和170米4个高度的风速和风向，因此共有8个特征分量，故j∈ [1,8]。
（2）距离d
距离用于反映风速的总体大小，即潜在风能的总体水平。x0的欧氏距离为
式中k表示每个样本在时间尺度上的数据量。本文对未来96h的天气过程进行功率预测，时间分辨率为15min，故每个样本在时间尺度上共有384组数据。v0, jk代表样本x0位于第j(j=1,2,…,8) 个特征分量第k(k=1,2,…,4τ) 个时间尺度的数据。
（3）极差R
极差如式（3）所示，其中v0,max为样本的最大风速、v0,min为样本的最小风速。
（4）方差D
方差如式（4）所示，其中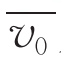
为样本的平均风速。方差和极差用以反映样本的波动水平。
（5）均值 
指代风速 3 次方的均值，计算公式如式（5）所示，用以表示潜在风功率。
1.2.2 相似度匹配
上述5个参数用以描述单个预测样本。为对比两个样本各参数之间相似度，将上述参数转化为3个相似度系数。
（1）相似度系数1（γi1）
γi1用以描述样本之间的趋势相似度，即相关性。式（1）所示ri(j) 为样本x0和xi在第j个特征分量的相关性，故可采用连乘法表示两个样本的综合趋势相似度，如式（6）所示。
采用连乘法可避免权重的分配问题。式中γi1越大，则待预测样本x0和第i个历史样本xi的趋势相似度越高。
（2）相似度系数2（γi2）
γi2表示两个样本间距离的相似度。依据式（2）计算两个样本之间的距离，如式（7）所示。
若只考虑式（6）所示的趋势相似度，则匹配到的两个样本虽然趋势相似，但风速幅值可能存在巨大的差异，即二者互为彼此的平移。故同时引入距离相似度，确保匹配到的相似样本在趋势上和风能幅值上均高度相似。
γi1的评判标准为其数值越大，则相似度越高。为统一度量标准，采用式（8）的形式定义距离相似度。γi2越大，则样本x0和xi之间的距离越接近。
（3）相似度系数3（γi3）
采用相似度系数γi1和γi2能为待预测样本匹配到变化趋势和风能幅值均高度相近的样本。为防止同时匹配到多个γi1和γi2均高度相似的历史样本，引入γi3对相似度最高的历史样本进行进一步筛选，如式（9）所示。γi3越大，则x0和xi之间的相似度越高。
至此，通过5个参数得到用以描述两组样本之间的3个相似度系数。
1.2.3 组合相似度匹配算法
在构建样本之间的相似度系数γi1、γi2和γi3后，需要同时考虑3个相似度系数，筛选出综合相似度最大的历史样本。为确保充分考虑各相似度系数，同时避免权重的分配问题，将γi1和γi2视作一级系数，进行第一轮检索，选出相似度较大的多个历史样本；将γi3视作次级系数，进行二次筛选，在高相似样本中进一步选出相似度最高的历史样本。
组合相似度匹配算法如图3所示，该算法分为3个阶段。
图3 组合相似度匹配算法流程图
阶段1 构建相似度系数γi1、γi2和γi3。依据式(1)~(9)，采用来自待预测样本的5个参数计算与各历史样本的相似度系数。
阶段2 检索一级系数γi1和γi2。历史样本中γi1自大到小排列，前5%的历史样本构成集合C1；γi2自大到小排列，前5%的历史样本构成集合C2。如果C1和C2仅有一个共同样本，则该样本即为待预测样本的历史最相似样本。
阶段3 检索次级系数γi3。若C1和C2有多个共同样本，则C1和C2的交集中γi1×γi2自大到小前50%的历史样本构成集合C3；若C1和C2无共同样本，则C1和C2的并集中γi1×γi2自大到小前25%的历史样本构成集合C3。历史最相似样本为集合C3中次级系数γi3最大的历史样本。
1.3 基于深度学习模型自适应选择的短期功率预测
在完成历史最相似样本的匹配后，由于历史样本的实际功率已知，故可通过各模型对历史最相似样本的预测误差来评估模型的适用性。本文采取MAE 作为适用性的评价指标，模型适用性评估的方式为，采用各深度学习模型对与待预测样本相对应的历史最相似样本分别进行功率预测，得到各模型的功率预测结果；进一步计算各模型的预测 MAE，MAE最低的模型即为历史最相似样本的最适模型，故认为该最适模型同时也是待预测样本的最适模型，并采用该最适模型对待预测样本进行功率预测。
本文选取当下4个较为热门的深度学习模型验证所提方法，分别是LSTM、BLSTM、CNN、SDAE。LSTM与BLSTM代表善于处理序列相关数据的深度神经网络，CNN代表善于处理网格数据的深度神经网络，SDAE 代表无监督深度学习模型；此外，BPNN也被用于构建模型库，代表用于处理大量数据的普通深度神经网络。
本文采取宁夏地区和吉林地区的两座风电场进行算例分析。数据自2017年1月1日至2018年12月31日共2年，时间分辨率为15min。训练集、验证集、测试集的比例为6:2:2，历史样本库与训练集相同。深度学习预测建模的输入数据包含NWP中的空间风速数据，以及来自SCADA系统的前4h实测历史功率。采取文献误差评价指标RMSE和MAE对所提方法进行评估。
2.1 算例 1——宁夏风电场
依据所提基于多参数风过程匹配与深度学习模型自适应选择方法对宁夏风电场进行功率预测，并与仅采用单一深度学习模型进行对比，功率预测曲线如图4所示。图中命名为“自适应方法”的曲线，即为本文所提方法的功率预测结果。图4（b）（c）（d）为对图4（a）中部分结果的放大。为便于观测区别，图4（e）（f）（g）为与图4（b）（c）（d）对应时段的各方法预测结果与实际值的绝对偏差。
从图4中可以看出，所提方法的功率预测曲线相较BPNN、LSTM、BLSTM、CNN、SDAE更接近实际值。所提基于多参数风过程匹配与深度学习模型自适应选择方法，能追踪预测MAE最低的深度学习预测模型，即采用最适合的深度学习模型为各待预测样本进行功率预测建模。
图4 各模型功率预测曲线对比
采用测试集进行误差分析，表1为宁夏风电场24h日前和96h短期的功率预测误差。从中可以得出的结论为，无论是24h日前预测的RMSE还是 MAE，本文所提方法均能保持最低误差；96h短期预测中自适应方法同样能保持最高精度。相较仅采用单一深度学习模型，24日前预测误差能降低0.29%~0.92%，96h短期预测误差能降低0.08%~1.12%，证实了本文所提方法能够提升预测精度。
表1 宁夏风电场各模型的短期预测误差
图5为以小时为分辨率得到的各模型预测误差，下方为自适应方法误差处于最低或较低时的时间区间。可以看出所提自适应方法在多数时段能保持较优的预测精度，同样证实了方法的有效性。图5 宁夏风电场各模型的短期预测误差
2.2 算例2——吉林风电场
表2为吉林风电场采用各预测模型得到的24h日前和96h短期的功率预测误差。在吉林风电场中所提方法同样能保持最佳精度。相较仅采用单一深度学习模型，24h日前预测误差能降低0.24%~0.61%，96h短期预测误差能降低0.07%~0.58%。
表2 吉林风电场各模型的短期预测误差
图6为吉林风电场以小时为分辨率得到的各模RMSE和MAE，同样表明了所提自适应方法在多数时段能保持较优的预测精度，证实了方法的有效性。
