M-K(Mann-Kendall)法是一种气候诊断与预测技术,可以判断气候序列中是否存在气候突变,如果存在,可确定出突变发生的时间。Mann-Kendall检验法也经常用于气候变化影响下的降水、干旱频次趋势检测。由于最初由曼(H.B.Mann)和肯德尔(M.G.Kendall)提出了原理并发展了这一方法,故称其为曼—肯德尔(Mann-Kendall)法。
1 原理
- 对于一个含有 n 个样本的时间序列 x,构造秩序列 :
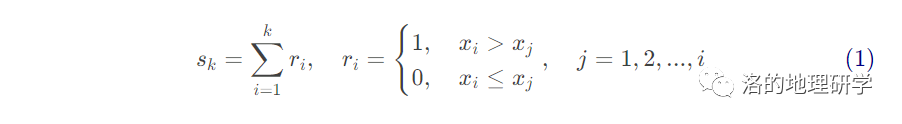
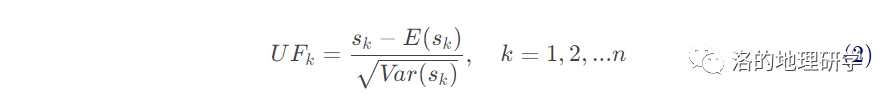
其中:
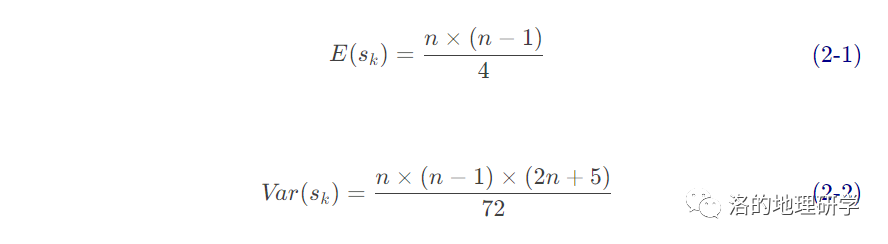
- 将序列 x 倒序,重复上述步骤,获得倒序下的 ,计算 :
<0,说明持续减少趋势,值在 0.05 显著性水平线内,说明通过0.05显著性检验
和 曲线的交点在置信水平区间[-1.96 1.96]内,并且确定交点具体年份,说明该年份参数呈现突变性增长状态;
如果交点不位于检验范围内,说明交点没有通过0.05 的检验,所以该年份参数突变性不具有突变性
2 代码思路
这里建立一个随机序列来模拟代码数据处理过程。
import numpy as np
np.random.seed(0)
Data = np.random.uniform(size = 72)
公共参数准备:
根据公式 2-1 和 2-2,E 和 Var 仅与数据序号 n 有关,因此,这里先准备 E 和 Var。
参考网上的解释:i 从2开始,根据统计量UFk公式,i=1时,Sk(1)、E(1)、Var(1)均为0,此时UFk无意义,因此公式中,令UFk(1) = 0
# 对时序数据 X ,生成一个序号序列,次数列范围为 2 ~ n。
# i 从 2 开始(即第二个数,其编号为 1,此时 1 处没有必要进行计算,因为其之前没有数据,所以这里从 2 开始生成)
NUMI = np.arange(2, len(Data))
# 计算 E
E = NUMI * (NUMI - 1) / 4
# 计算 Var
VAR = NUMI * (NUMI - 1) * (2 * NUMI + 5) / 72
第一步:正序计算
# 1.计算 Ri。即:序列中的某一个值与此值之前的所有值以此相比,结果为大出现的次数。
Ri = [(Data[i] > Data[1:i]).sum() for i in NUMI]
# 2.计算 Sk。使用 numpy 累计求和函数 cumsum。
Sk = np.cumsum(Ri)
# 3.计算 UFk。考虑到 i 从 2 开始,因此把未计算的两个位置填充 0 。
UFk = np.pad((Sk - E) / np.sqrt(VAR), (2
,0))
第二步:倒序计算
# 思路参考第一步,这里进行简写。
## 对于倒序,由于 Python 支持传入负数表示倒序取值,这里利用此特性直接生成倒序(反向) Bk,不包含最后一个数(编号 -1)。
Bk = np.cumsum([(Data[i] > Data[i:-1]).sum() for i in -(NUMI+1)])
## 按照 UFk 的计算方法后取负数即为 UBk。由于本身未对 Data 进行倒序,这里计算完成后对数据进行倒序。
UBk = np.pad((-(Bk - E) / np.sqrt(VAR)), (2,0))[::-1]
3 绘图
import matplotlib.pyplot as plt
# 配置参数
PAR = {'font.sans-serif': 'Times New Roman',
'axes.unicode_minus': False
}
plt.rcParams.update(PAR)
plt.figure(figsize = (10, 5.5), dpi = 300)
plt.plot(range(1 ,len(Data)+1),UFk,label = 'UFk',color = 'orange')
plt.plot(range(1 ,len(Data)+1),UBk,label = 'UBk',color = 'cornflowerblue')
plt.grid(True, linestyle = (0,(6,6)), linewidth = 0.4)
## 画出 0.05 置信区间边界
x_lim = plt.xlim()
plt.plot(x_lim,[-1.96,-1.96],linestyle = (0,(6,6)),color = 'r')
plt.plot(x_lim, [0,0],linestyle = (0,(6,6)))
plt.plot(x_lim,[1.96,1.96],linestyle = (0,(6,6)),color = 'r')
plt.legend(frameon = False)
plt.show()
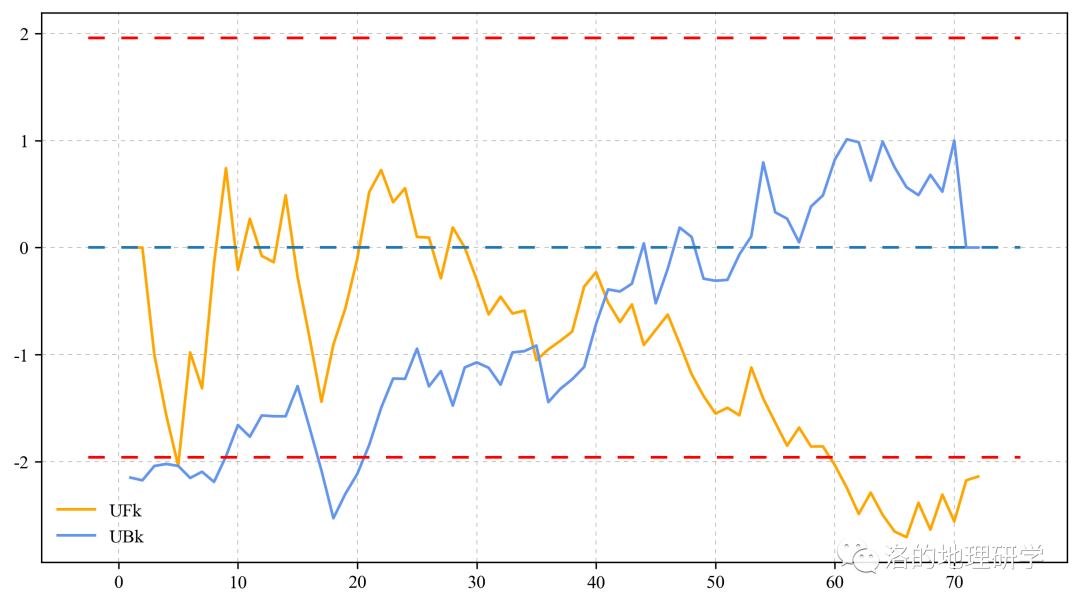 请添加图片描述
请添加图片描述4 后续
- gma 会在 1.0.12 版本合入此算法,并对其进行扩展。欢迎各位使用、反馈和讨论。