
胶体自组装(胶体自发地组织成有序结构)策略被认为是生产下一代材料的关键。然而,当今种类繁多的胶体积木和无限的热力学条件使得系统的探索变得困难。这一领域的真正挑战是扭转这一逻辑,开发一种健壮的、通用的算法来反向设计自组装成目标结构的胶体。
来自荷兰乌得勒支大学的Gabriele M. Coli团队介绍了一种通用的逆向设计方法,通过瞄准晶体、准晶和液晶的衍射图案来有效地对它们进行逆向工程。本文的算法依赖于参数优化的进化策略和卷积神经网络作为序参数的协同使用,并为实验上可行的胶体相互作用的逆向设计提供了一条前进的道路,特别是优化以稳定所需的结构。相关工作以题为“Inverse design of soft materials via a deep learning–based evolutionary strategy”的研究性文章在《Science Advances》上发表。

CNN算法
受通过散射模式识别相位的成功经验和机器学习的进步的启发,本文从一个新的途径来解决这个问题,直接使用结构因子的编码作为序参数。为此,本文训练卷积神经网络(CNN)来根据不同的衍射图案对不同的相位进行分类,并使用结果来构造适应度函数,使得被分类为目标相位的可能性较高的配置将以较高的适应度得分。最终算法的流程图如图1所示。关于基于CNN的适应度函数选择的详细讨论可以在补充材料中找到。结果表明,该算法具有极强的鲁棒性和通用性,不仅方便了晶相和液晶相的逆设计,而且方便了QC的逆向设计,因为QC的非周期性是出了名的难以逆向设计。该方法以代或迭代的方式进行,基本上由三个步骤组成:(i)采样、(ii)适应度评估和(iii)更新。
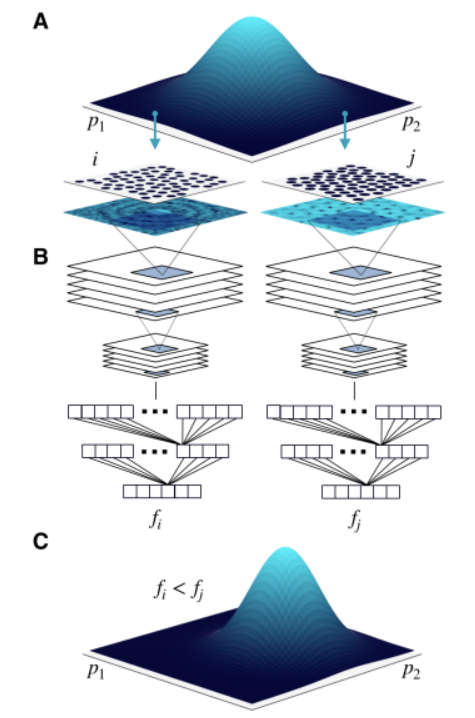
图1.每一代执行的三个步骤的示意图。
HCSS模型中QC12的逆向工程
本文从考虑肩宽δ=1.4σ的固定值的HCSS模型开始本文的研究,在这个值下QC12相已经被证明是稳定的。相图作为温度和压力的函数如图2A所示。逆向工程过程的结果汇总在图2中。从以流体相稳定区域为中心的高斯开始逆向工程过程,算法到达目标QC12在大约25代内稳定的区域。图2A显示了温度kBT/ϵ和压力βPσ2平面上的多元高斯分布在连续几代中的演化。图2B显示了在上一代(第100代)中获得的代表性照片,而相应的以12次旋转对称为特征的衍射图案如图2C所示。该算法的成功在很大程度上依赖于CNN发现系统中哪怕是微小的结构变化的能力。在逆向工程过程的早期相,当系统处于流体相时,算法已经发现通过增加压力和密度来增加整体结构有序性是很方便的。这可以在图2D中清楚地看到,在图中本文绘制了所有样本的平均适应度的演变情况。虽然早期世代的适应度变化很小,但它们足以引导进化策略朝着正确的方向发展。

图2.HCSS模型中QC12的逆向工程
HCSS模型中QC12、QC10和QC18的逆向工程
逆向工程过程的结果总结在图3中。特别地,图3(A到C)显示了当目标为(i)QC12、(ii)QC10和(iii)QC18时多变量高斯分布的演化。根据要找到的QC,分布向不同方向演化,并最终收敛到不同的状态点。在所有情况下,获得的压力和肩宽的最终值与三个QC被证明是稳定的值非常一致。本文还获得了具有代表性的QCs照片,其衍射花样如图3(D至F)所示。每个衍射图案被确认存在正确的准晶结构。
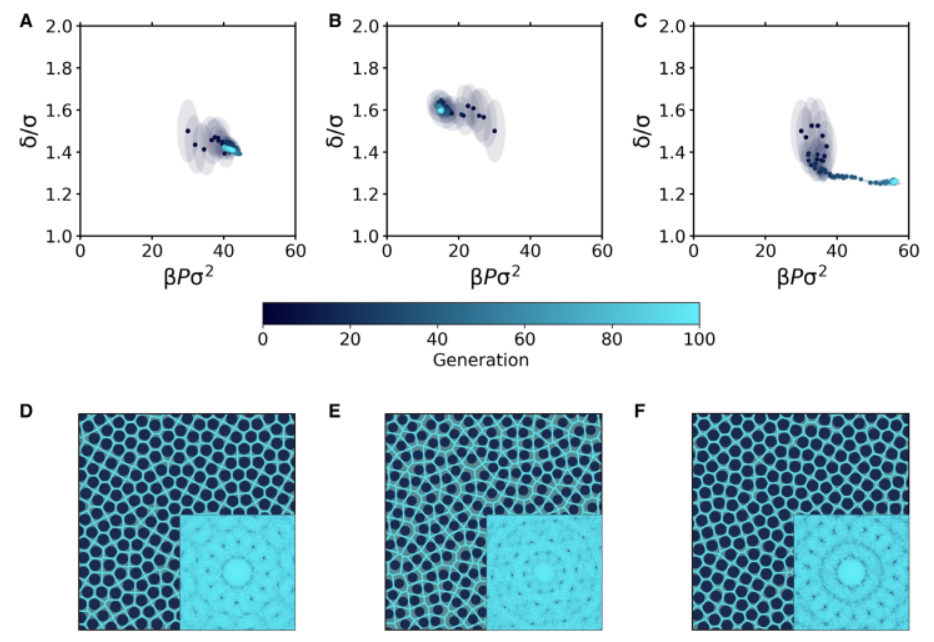
图3.HCSS模型中QC12、QC10和QC18的逆向工程
在一种新模型交互中的应用
为了测试本文的方法在新类型的交互上有效的能力,本文使用在HCSS模型上训练的同一个CNN对SCS模型中的QC12进行逆向工程。类似于HCSS情形,本文保持相互作用参数不变,即δ=1.35σ和kσ=10,并使进化策略找到QC12稳定的密度和温度区域。图4A中的相图被用作评估和监测该方法的性能的参考。逆向工程过程的结果总结在图4中。图4A显示了温度-密度平面中多元高斯分布的演化。从以流体区域为中心的分布开始,算法立即开始增加密度和降低温度以增加整体顺序。令人印象深刻的是,仅仅五代之后,分布的平均值已经在QC12的稳定区域内,这表明了CNN对相互作用势的变化的稳健性。在剩下的世代中,分布的协方差缩小,平均温度向相图中的较低温度移动。图4(B和C)分别显示了在上一代中获得的QC12的代表性照片及其衍射图。
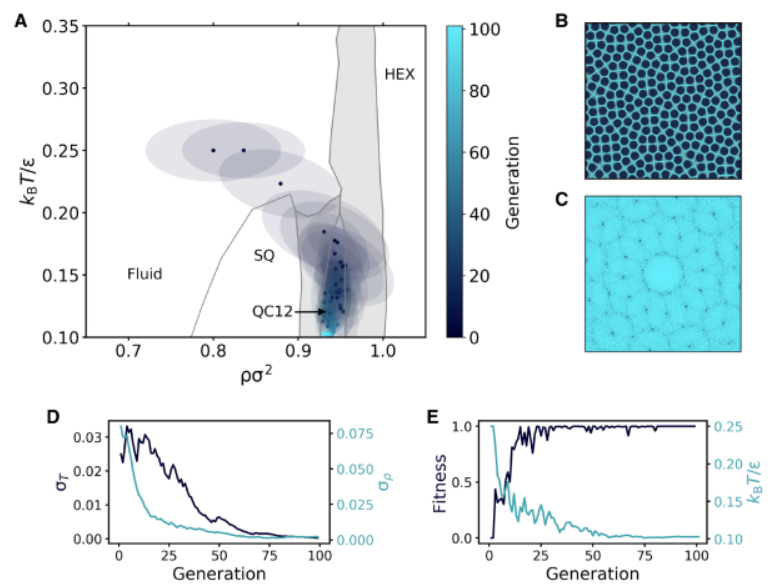
图4.SCS模型中QC12的逆向工程
相位的发现
逆向工程过程的结果汇总在图5中。进化策略从流体相开始,降低温度,增加压力和肩宽,以最大限度地适应环境(图5C到F),为该系统找到尚未预测的QC10相。作为算法已进一步找到QC10并进行确认,图5B示出了在上一代期间获得的代表性照片以及相应的衍射图案。因此,本文的算法成功地定位了SCS模型中的一个新相。
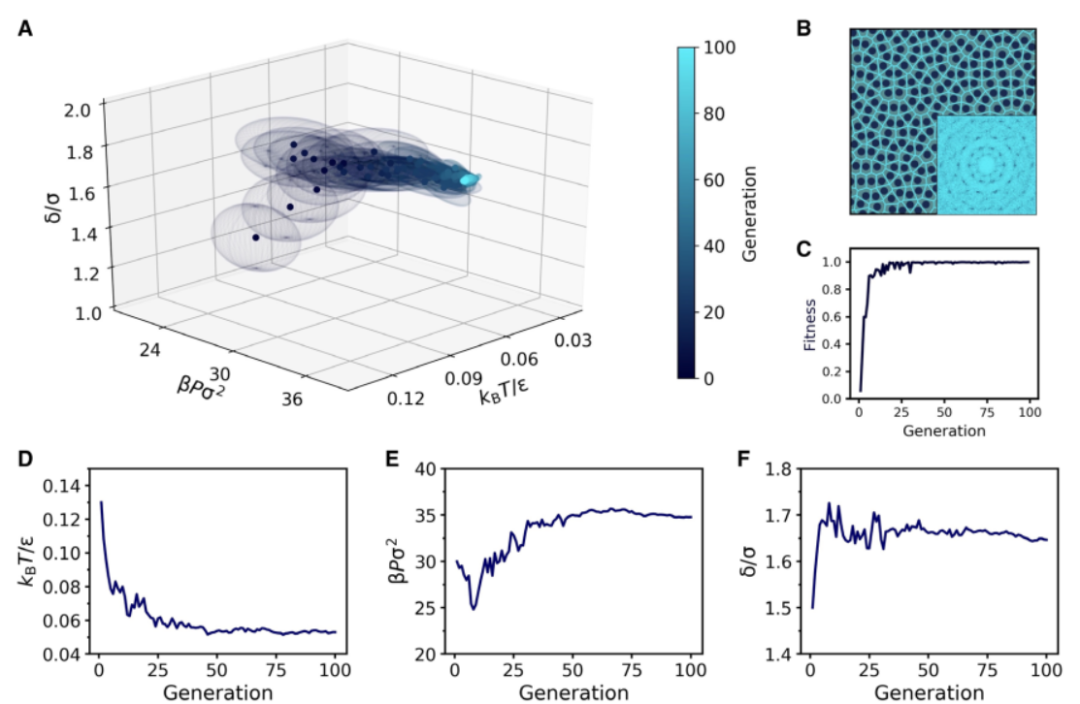
图5.在SCS模型中发现QC10。
从实用的角度来看,将本文的方法扩展到3D情况是特别有意义的。2D衍射图案立即提供了即使用肉眼也很容易读取的结构信息,而3D衍射图案则更难解释。因此,要处理3D系统,通常需要将粒子坐标投影到具有相关对称性的平面上。当使用CNN时,由于其固有的架构,这一方面变得无关紧要,因为CNN能够自然地处理完整的3D信息。
链接:
https://www.science.org/doi/10.1126/sciadv.abj6731
本文由SSC供稿。