深入浅出 Python 中的递归算法

一、初识递归

递归（Recursion）是一种解决问题的思路，其精髓在于将问题分解为规模更小的相同问题，持续分解，直到问题规模小到可以用非常简单直接的方式来解决。递归的问题分解方式非常独特，其算法方面的明显特征就是：在算法流程中调用自身。

递归为我们提供了一种对复杂问题的优雅解决方案，精妙的递归算法常会出奇简单，令人赞叹，妙啊！

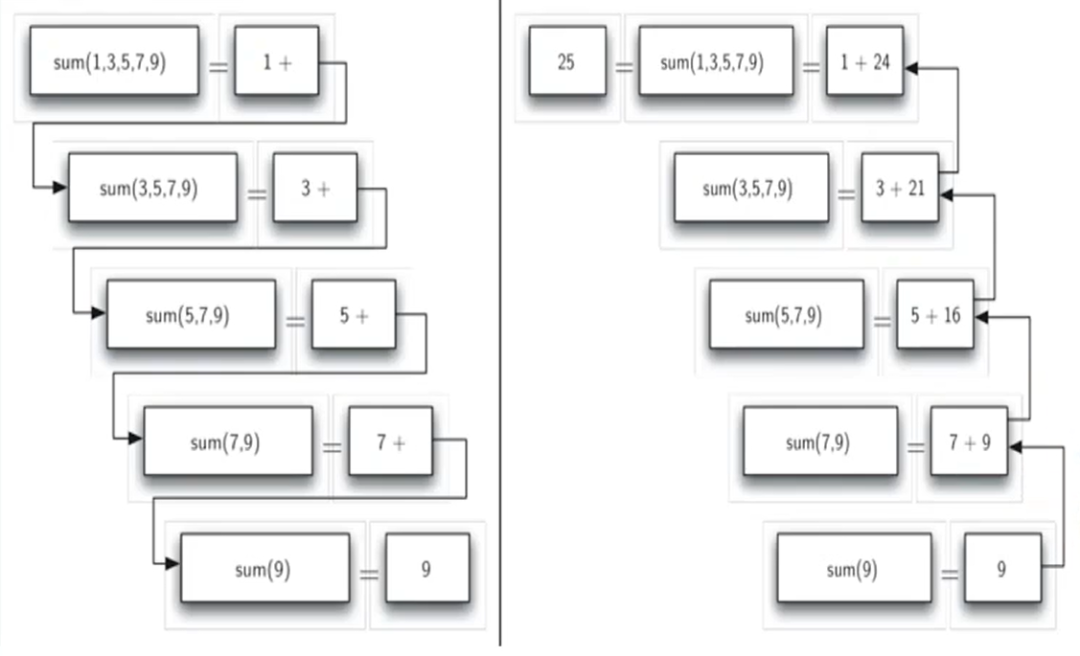
举例：给定一个列表，返回其中所有数的和，列表中数字的个数未知，现在既不能用 for 循环，也不能用 while 循环，这时可以用递归的方法来解决问题！

• 数列求和问题具备了基本结束条件：当列表长度为 1 的时候，直接输出所包含的唯一数。
• 数列求和处理的数据对象是一个列表，而基本结束条件是长度为 1 的列表，那递归算法就要改变列表并向长度为 1 的状态演进，代码实现时具体做法是将列表长度减少1。
• 调用自身：实际上可以理解为"问题分解成了规模更小的相同问题"，在数列求和算法中就是"更短数列的求和问题"。

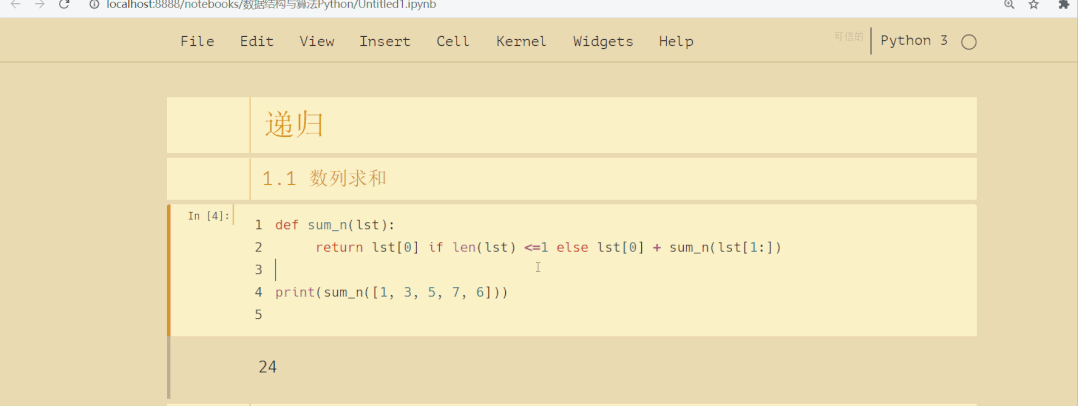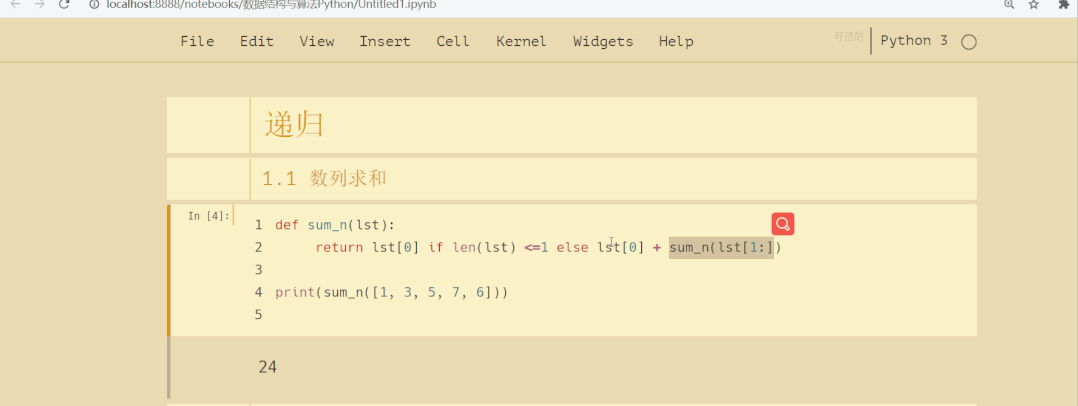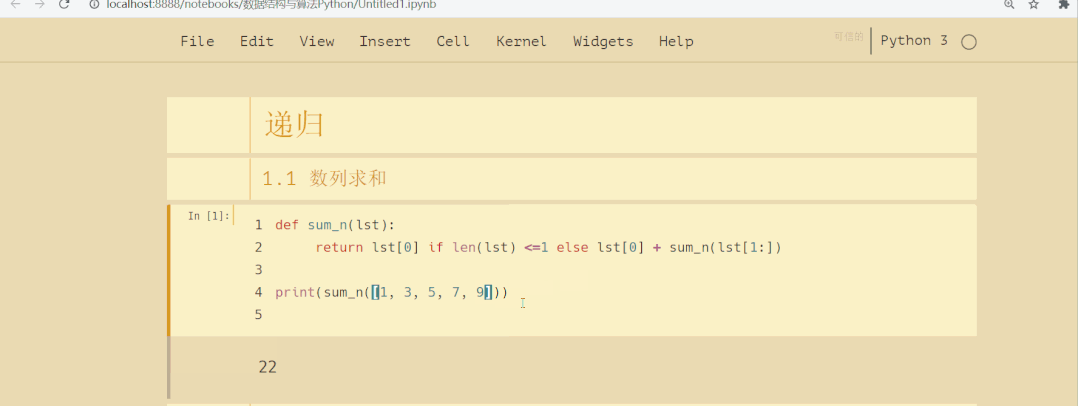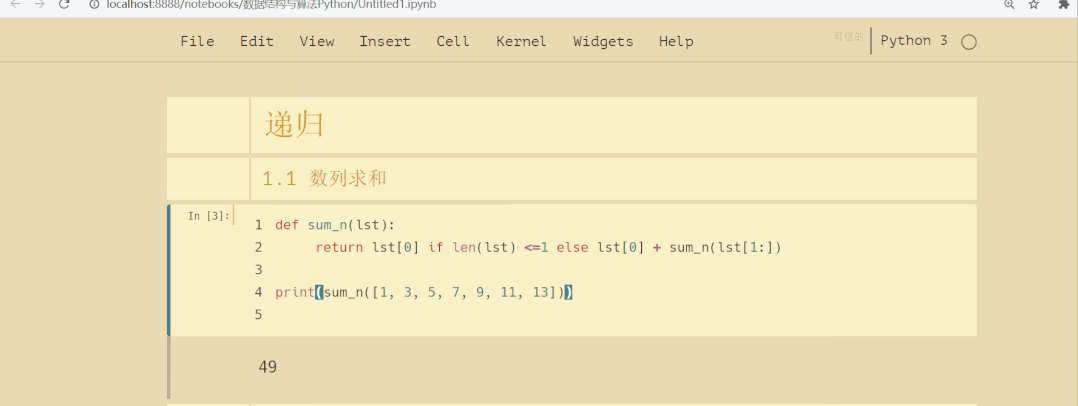
def sum_n(lst):
     return lst[0] if len(lst) <=1 else lst[0] + sum_n(lst[1:])

print(sum_n([1, 3, 5, 7, 9]))

• 递归算法必须要有结束条件（最小规模问题的直接解决）
• 递归算法必须能改变状态向基本结束条件演进（减小问题规模）
• 递归算法必须调用自身（解决减小了规模的相同问题）

• 当一个函数被调用的时候，系统会把调用时的现场数据压入到系统调用栈。每次调用，压入栈的现场数据称为栈帧，当函数返回时，要从调用栈的栈顶取得返回地址，恢复现场，弹出栈帧，按地址返回。
• 在调试递归算法程序的时候经常会碰到这样的错误：RecursionError: maximum recursion depth exceeded in comparison，原因递归的层数太多，但系统调用栈容量是有限的。

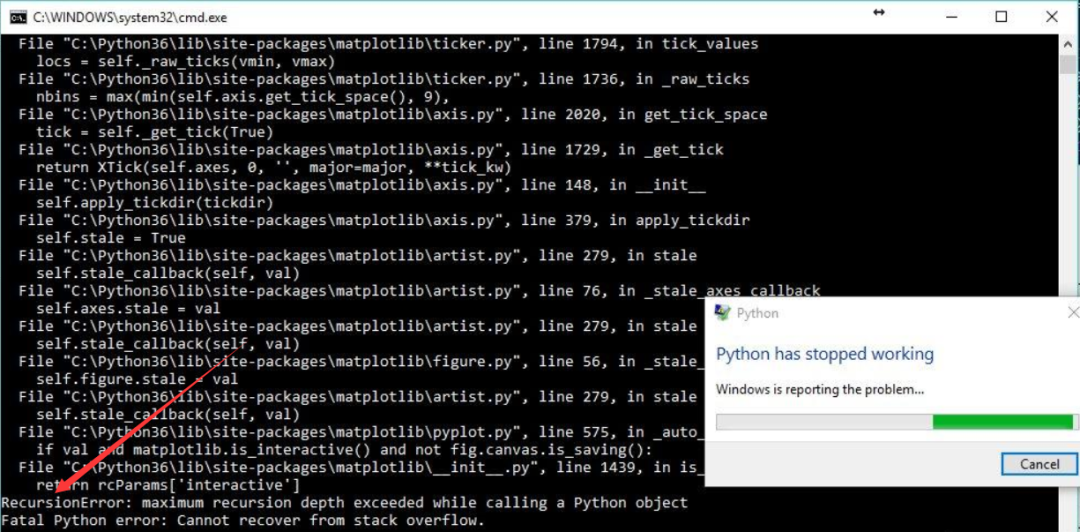
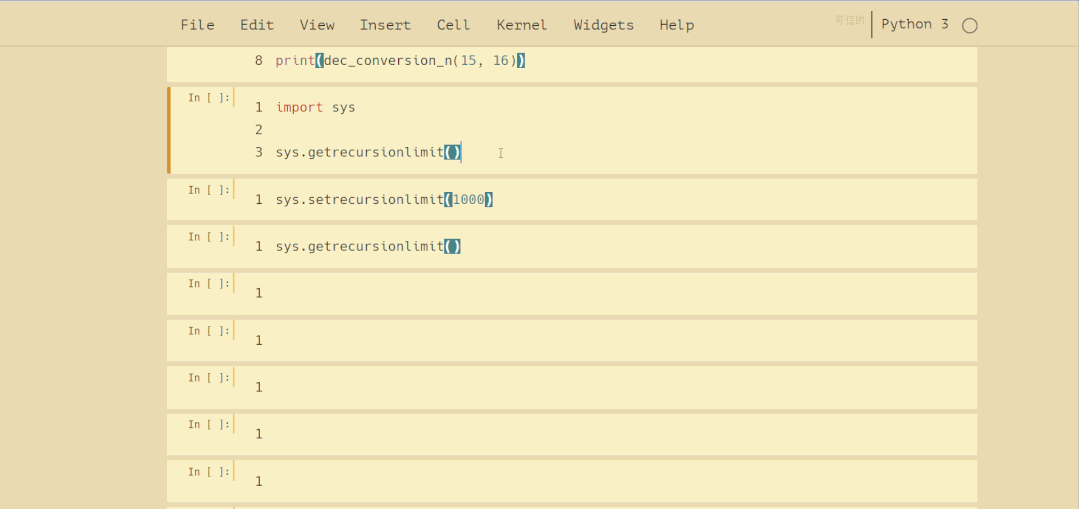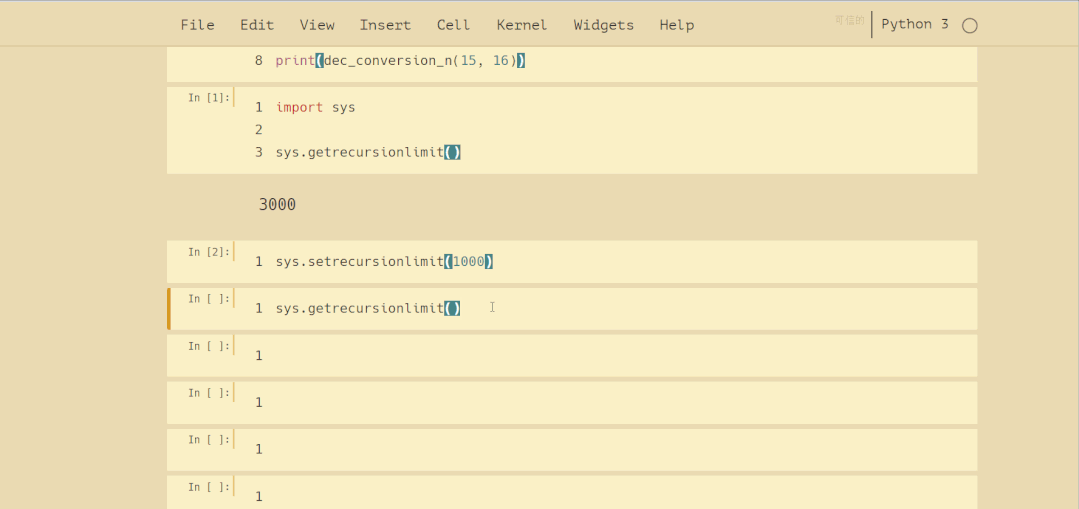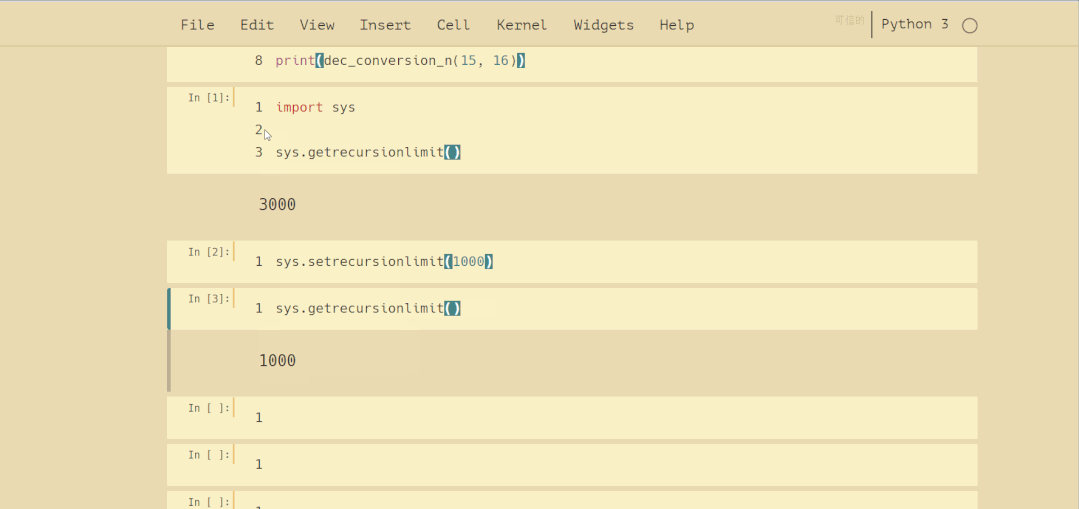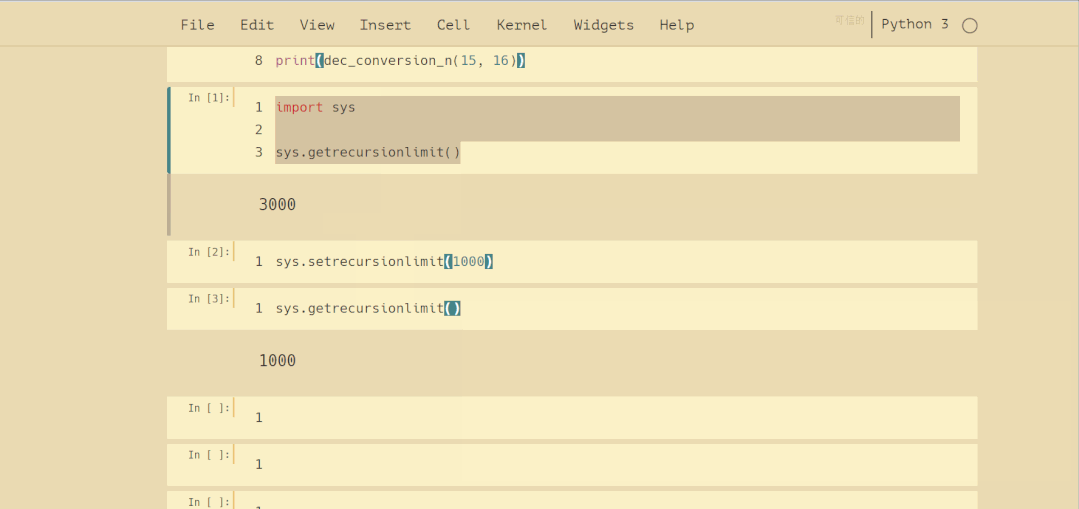
爆栈是非常危险的操作，在实际开发写递归算法时应尽力避免。Python内置的 sys 模块可以获取和调整最大递归深度，操作如下：

二、进制转换

• 十进制有十个不同符号：dec_str="0123456789"，比 10 小的整数，转换成十进制，直接查表就可以得到：dec_str[n]，把比 10 大的整数，拆成一系列比十小的整数，逐个查表，比如七百六十九，拆成七、六、九，查表就可以得到769。
• 所以，在递归三定律里，我们找到了 "基本结束条件”，就是小于 10 的整数拆解整数的过程就是向“基本结束条件”演进的过程"。
• 我们用整数除，和求余数两个计算来将整数一步步拆开，除以 "进制基base"（//base） 对 "进制基" 求余数（%base）

def dec_conversion_n(n, base):
    str_list = "0123456789ABCDEF"
    if n         return str_list[n]  # 到了最小规模  查表
    else:   # 减小规模  调用自身
        return dec_conversion_n(n // base, base) + str_list[n % base]

print(dec_conversion_n(233, 8))

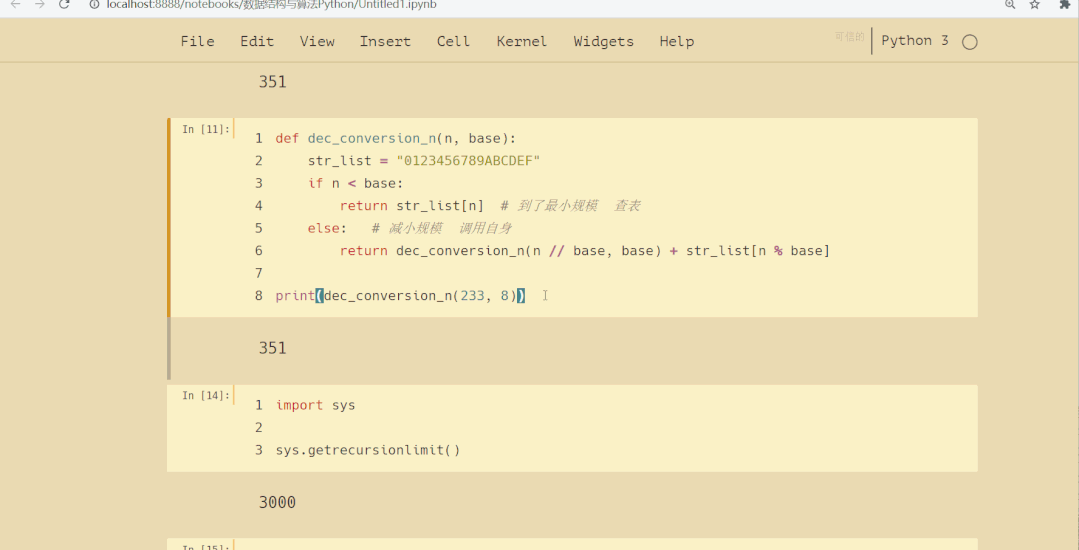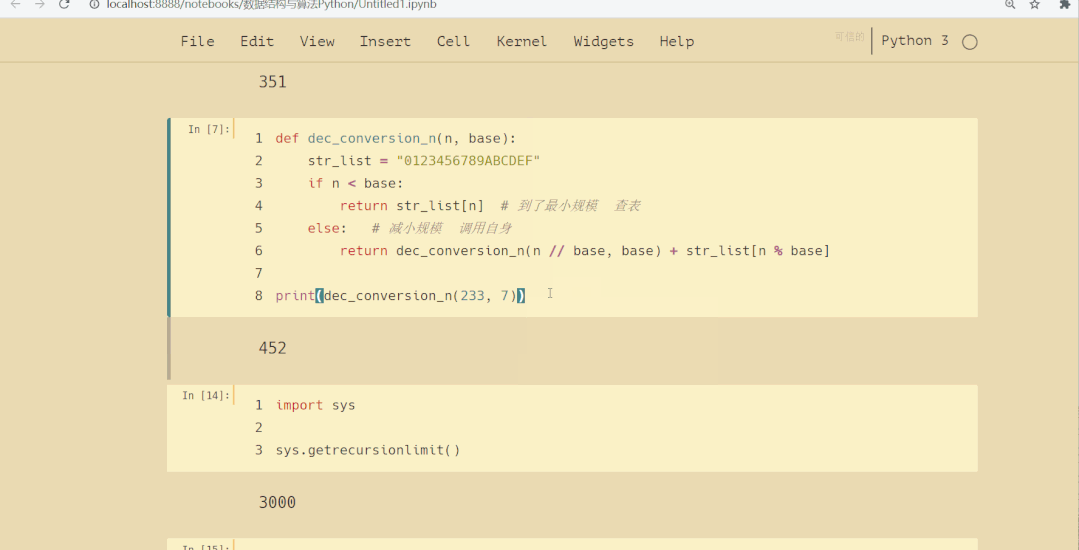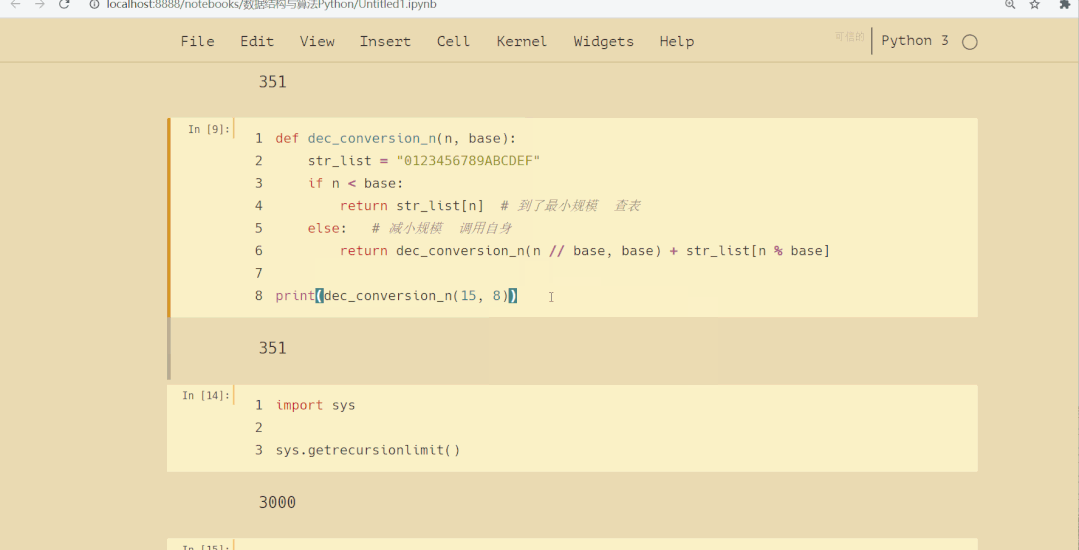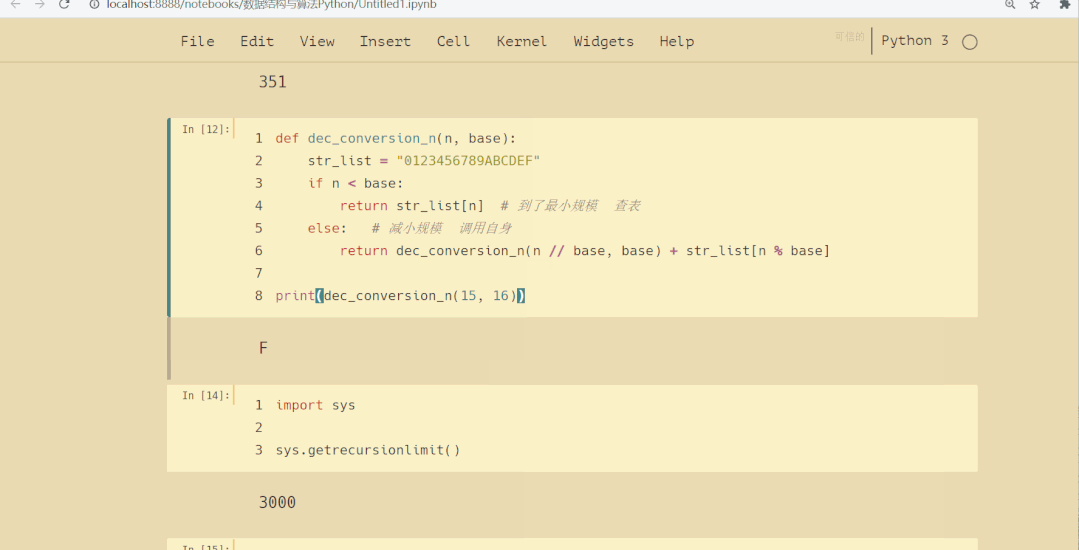
def dec_conversion_n(n, base):
    str_list = "0123456789ABCDEF"
    return str_list[n] if n else dec_conversion_n(n // base, base) + str_list[n % base]

print(dec_conversion_n(233, 8))

余数总是小于"进制基base"的，当整数商小于进制基时，达到递归结束条件，可直接进行查表转换，整数商成为 "更小规模" 问题，通过递归调用自身解决，成功利用递归的方法来解决进制转换问题。

三、递归可视化

import turtle

t = turtle.Turtle()
def draw_spiral(line_len):
    if line_len > 0:
        t.forward(line_len)
        t.right(90)
        draw_spiral(line_len - 5)

draw_spiral(160)
turtle.done()

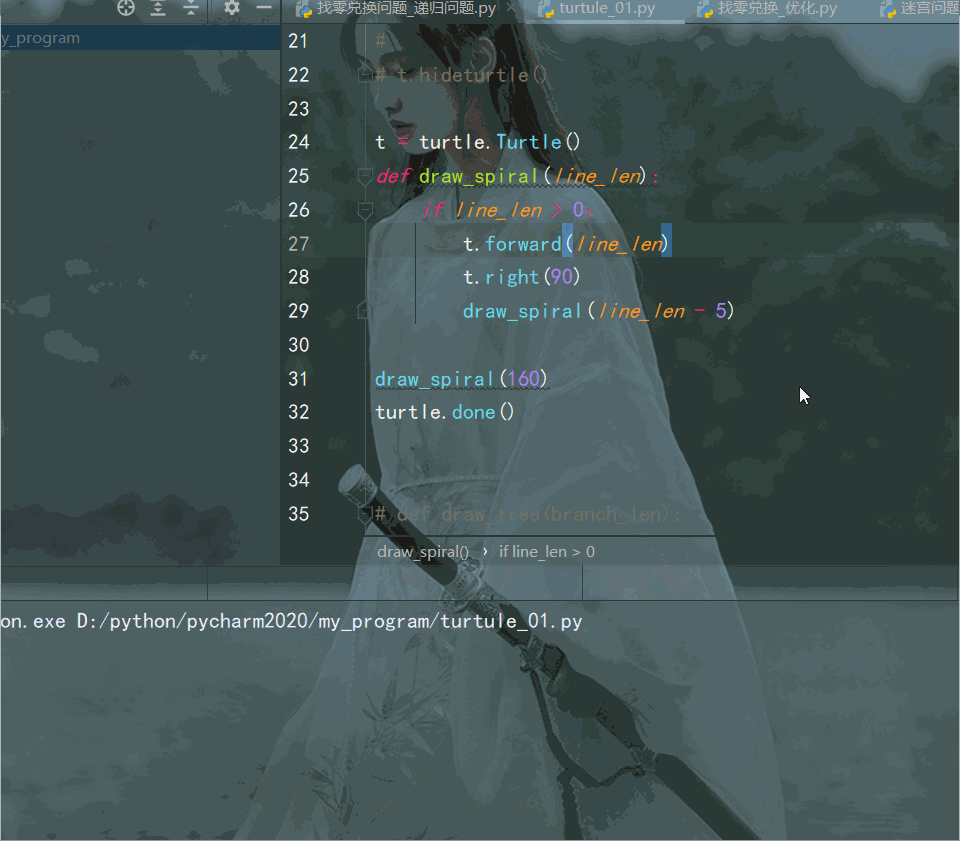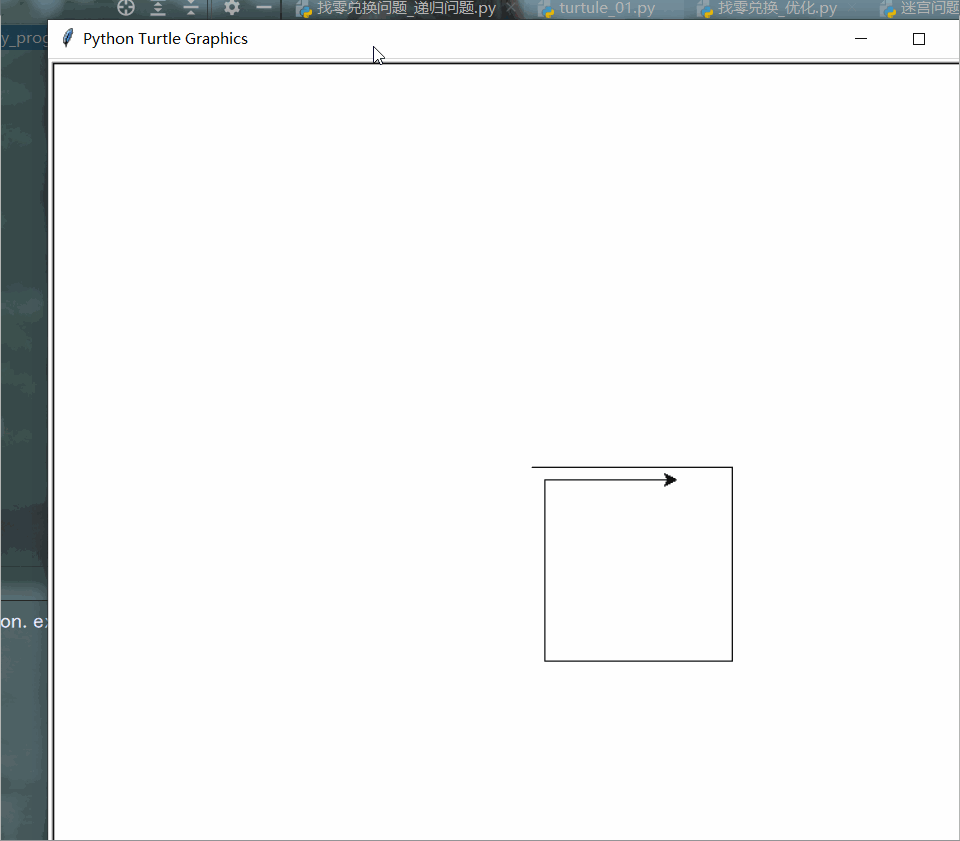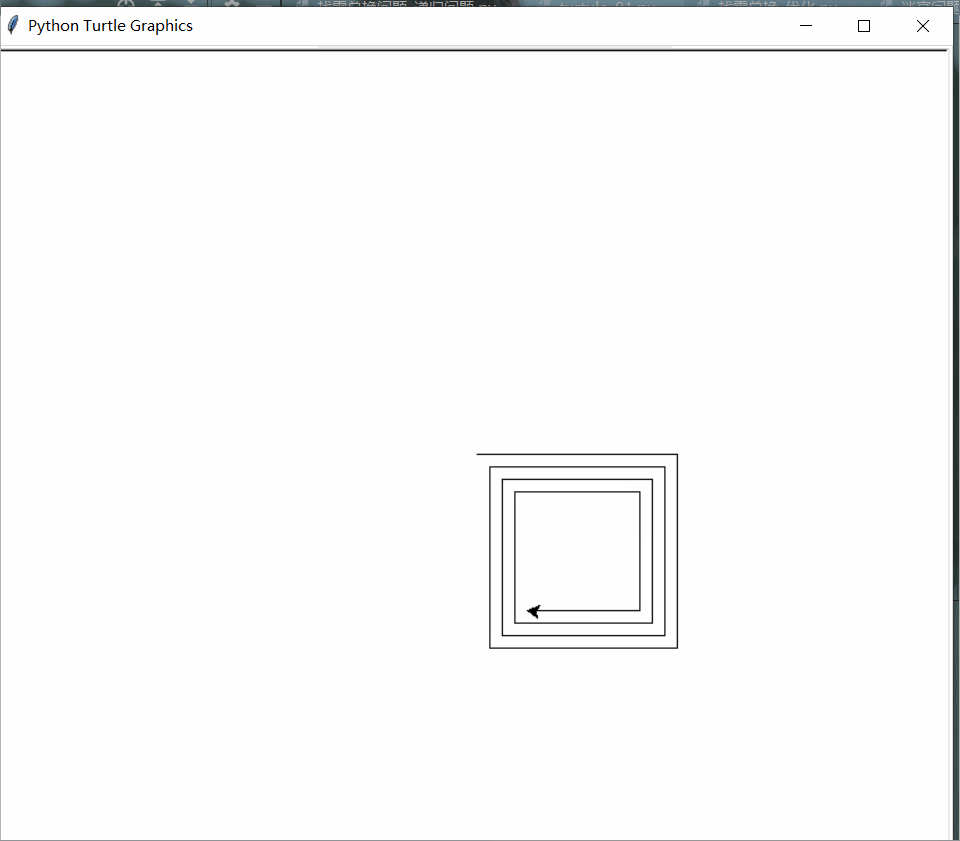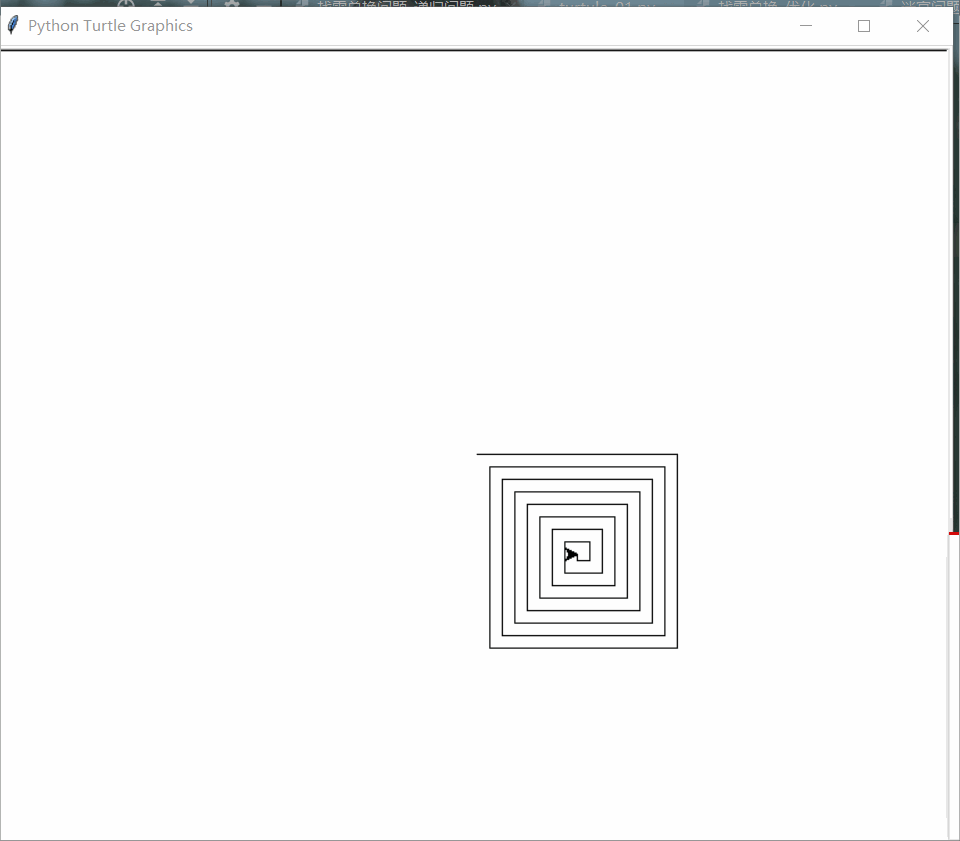用分形树能更形象地展现递归调用。分形是在不同尺度上都具有相似性的事物，分形树特征：子图结构与自身相似，很容易想到递归。Python中的 turtle 的使用，让我们能够很方便地画出分形树，画分形树的思想也可以用到二叉树的遍历中，代码实现如下：

def draw_tree(branch_len):
    if branch_len > 5:
        t.forward(branch_len)
        t.right(20)
        draw_tree(branch_len - 15)
        t.left(40)
        draw_tree(branch_len - 15)
        t.right(20)
        t.backward(branch_len)


t = turtle.Turtle()
t.left(90)
t.penup()
t.backward(100)
t.pendown()
t.pencolor('red')
t.pensize(2)
draw_tree(75)
t.hideturtle()
turtle.done()

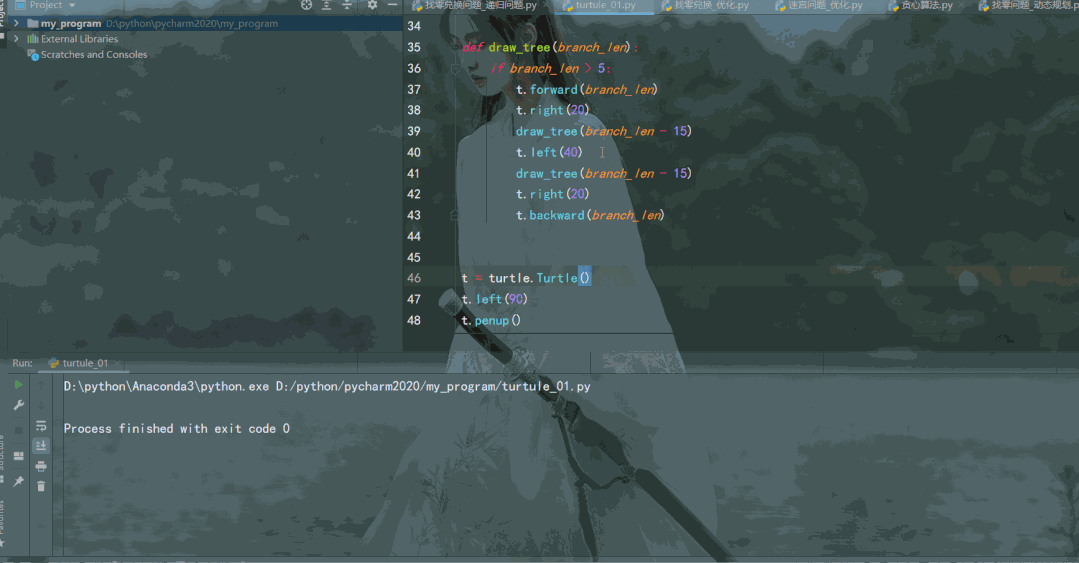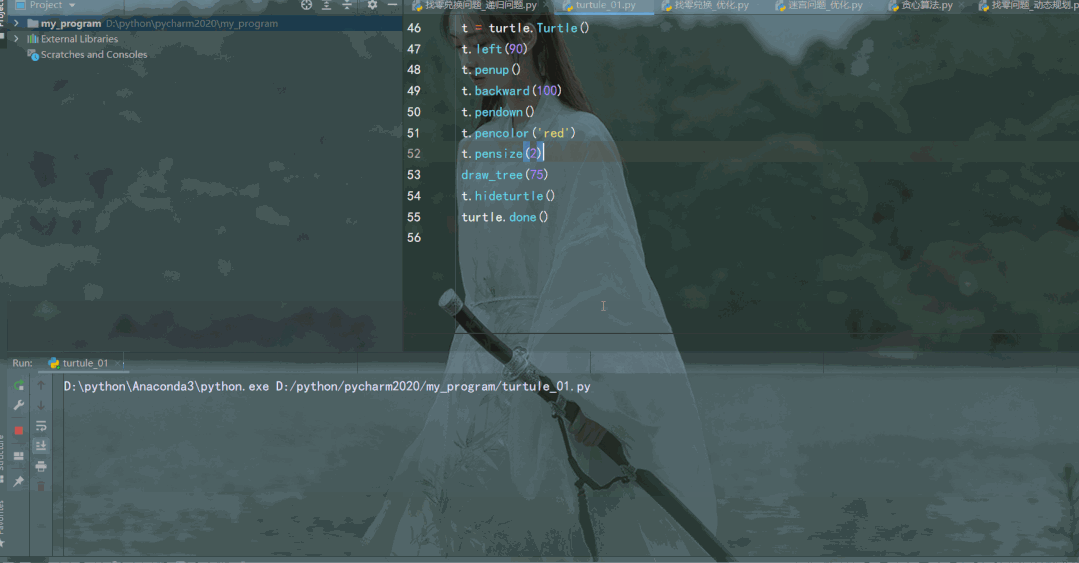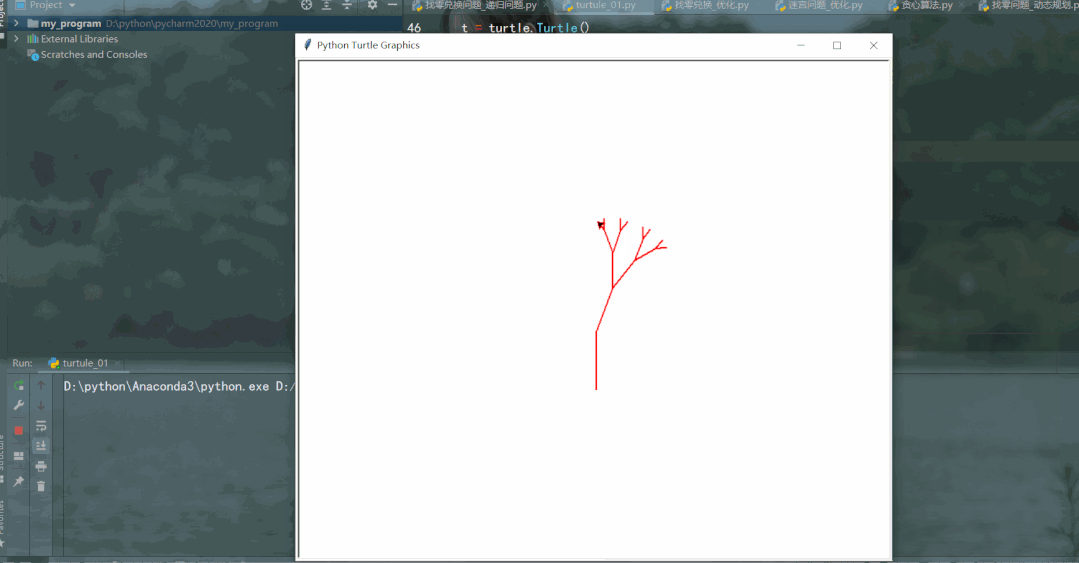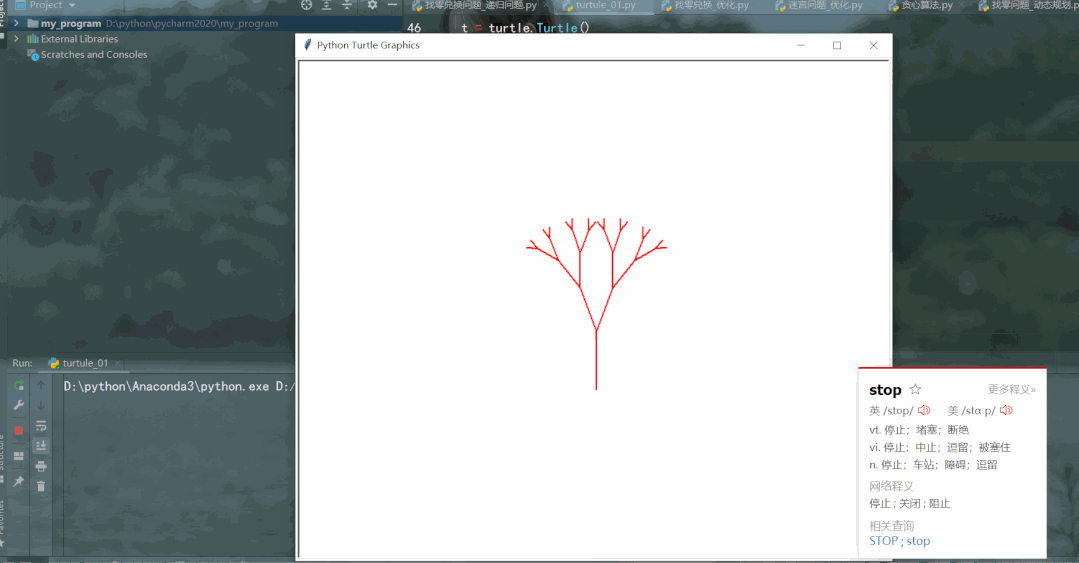把树分解为三个部分：树干、左边的小树、右边的小树分解后，正好符合递归的定义：对自身的调用。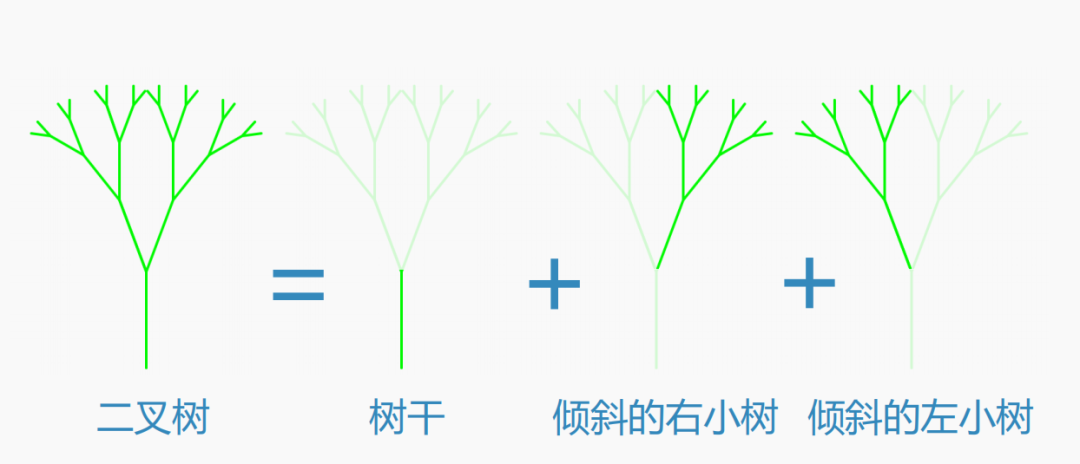

谢尔宾斯基三角形（英语：Sierpinski triangle）也是一种分形，由波兰数学家谢尔宾斯基在 1915 年提出，它是自相似集的例子。根据自相似特性，谢尔宾斯基三角形是由 3 个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成，由于我们无法真正做出谢尔宾斯基三角形（degree趋于无穷），只能做 degree 有限的近似图形。

在 degree 有限的情况下，degree=n的三角形，是由 3 个 degree=n-1 的三角形，按照品字形拼叠而成。同时，这 3 个 degree=n-1 的三角形边长均为degree=n的三角形的一半（规模减小）。当degree=0，则就是一个等边三角形，这是递归基本结束条件。作图如下：

    
# -*- coding: UTF-8 -*-
"""
@Author  ：叶庭云
@公众号  ：修炼Python
@CSDN    ：https://yetingyun.blog.csdn.net/
"""
import turtle


def drawTriangle(points, color, my_turtle):   # 绘制等边三角形
    my_turtle.fillcolor(color)
    my_turtle.up()
    my_turtle.goto(points[0][0], points[0][1])
    my_turtle.down()
    my_turtle.begin_fill()
    my_turtle.goto(points[1][0], points[1][1])
    my_turtle.goto(points[2][0], points[2][1])
    my_turtle.goto(points[0][0], points[0][1])
    my_turtle.end_fill()


def getMid(p1, p2):       # 取两个点的中心
    return (p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2


def sierpinski(points, degree, my_turtle):
    colormap = ['blue', 'red', 'green', 'white',
                'yellow', 'violet', 'orange']
    drawTriangle(points, colormap[degree], my_turtle)
    if degree > 0:
        sierpinski([points[0],
                    getMid(points[0], points[1]),
                    getMid(points[0], points[2])],
                   degree - 1, my_turtle)
        sierpinski([points[1],
                    getMid(points[0], points[1]),
                    getMid(points[1], points[2])],
                   degree - 1, my_turtle)
        sierpinski([points[2],
                    getMid(points[2], points[1]),
                    getMid(points[0], points[2])],
                   degree - 1, my_turtle)


def main():
    myTurtle = turtle.Turtle()
    myWin = turtle.Screen()
    myPoints = [[-100, -50], [0, 100], [100, -50]]   # 外轮廓三个顶点
    sierpinski(myPoints, 4, myTurtle)   # 画degree=5的三角形
    myWin.exitonclick()


main()

效果如下：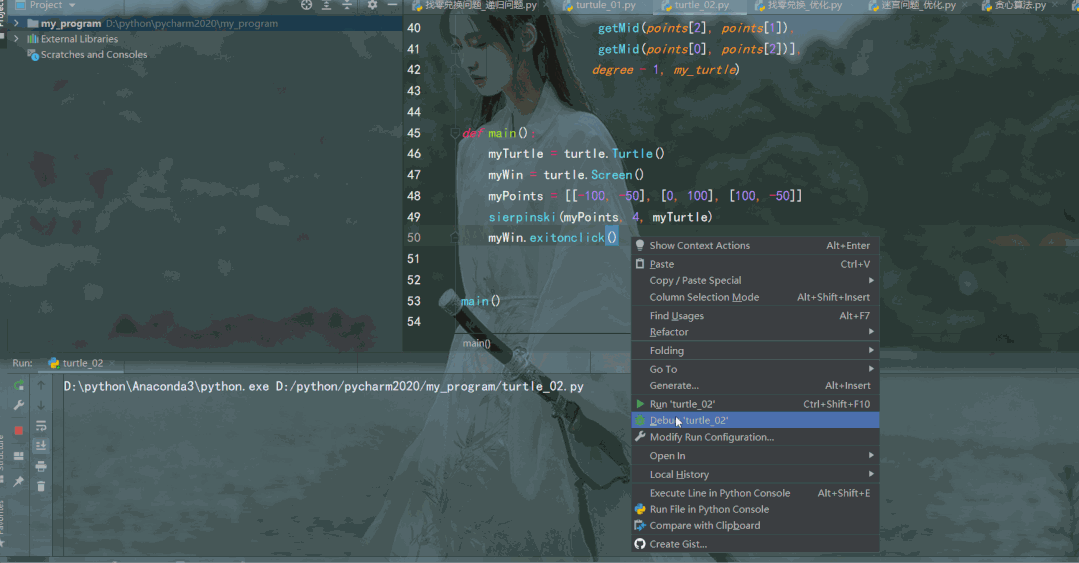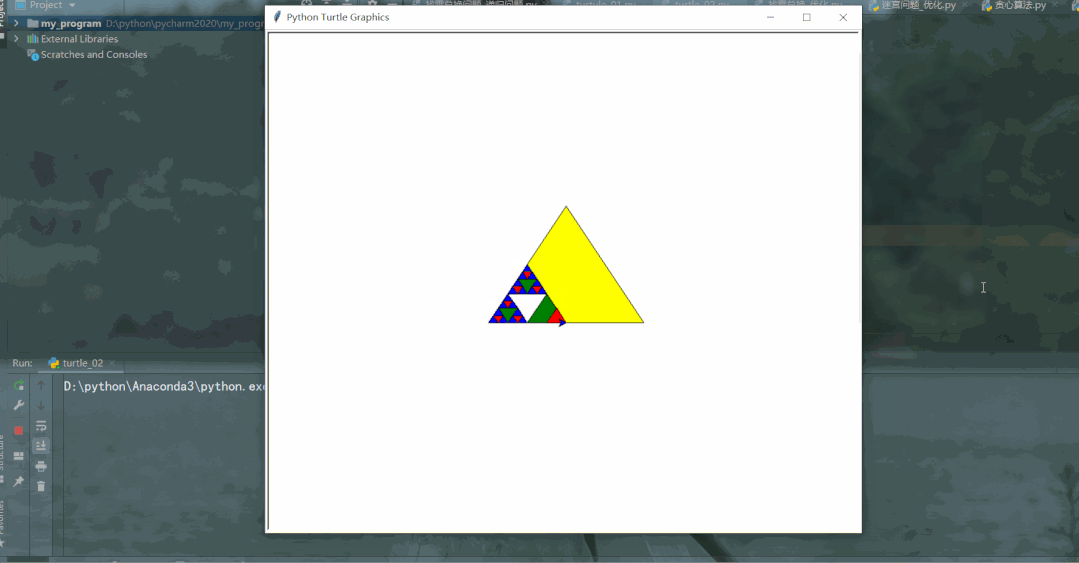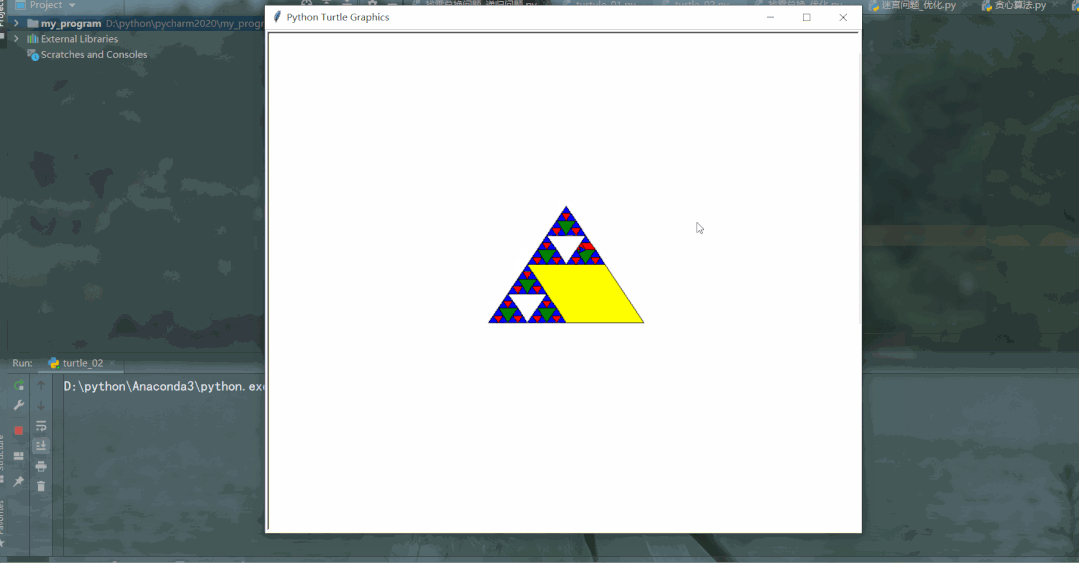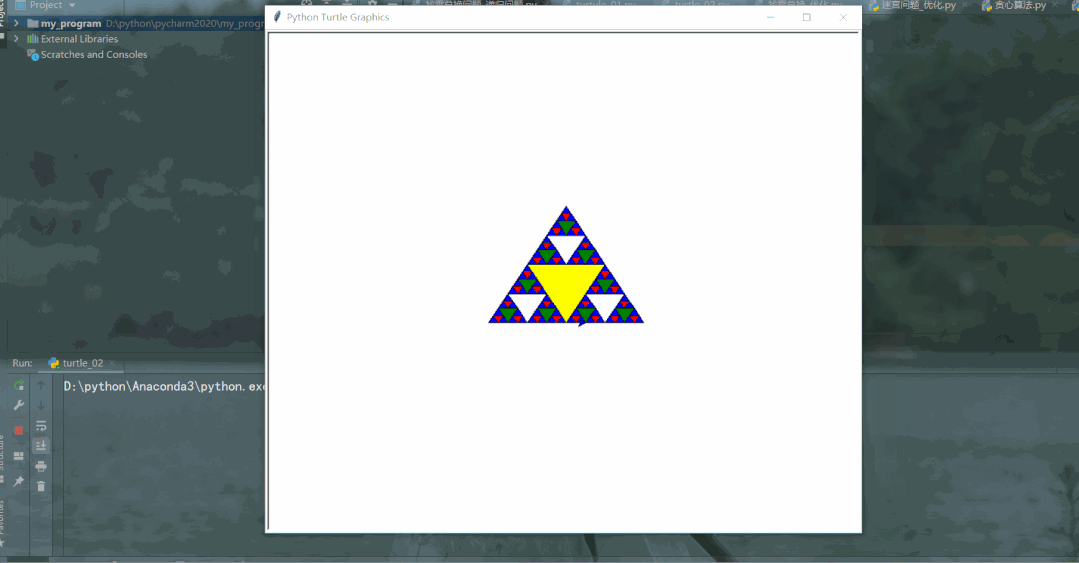

四、汉诺塔问题求解

问题来源：汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从上往下从小到大顺序摞着 64 片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘，只能移动在最顶端的圆盘。有预言说，这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。当然这个传说并不可信，如今汉诺塔更多的是作为一个玩具存在。

这里推荐一个可以在线玩汉诺塔小游戏的网站：http://www.htmleaf.com/Demo/201508272485.html

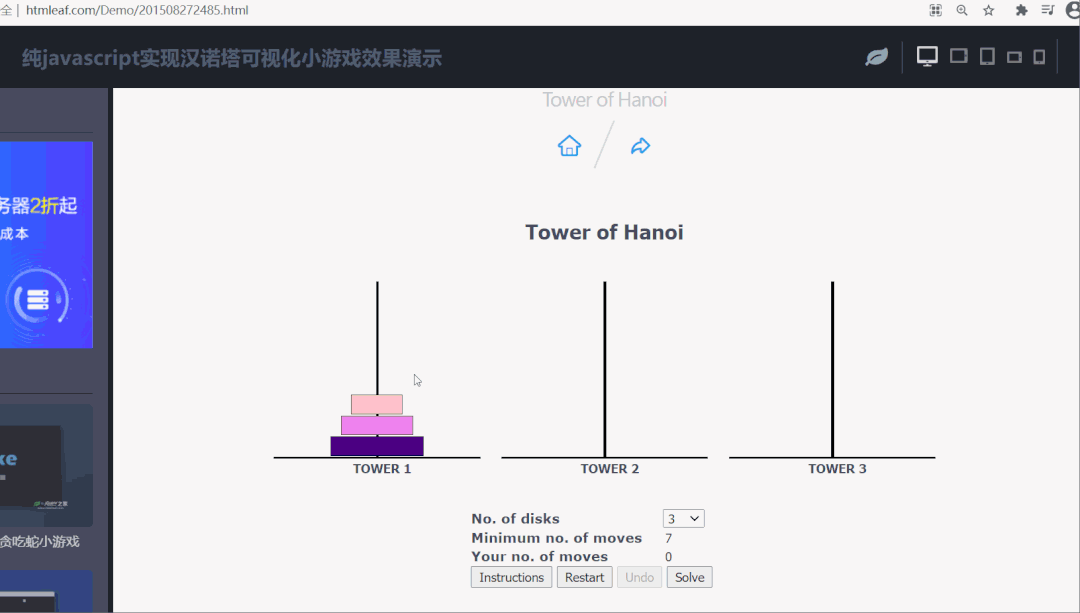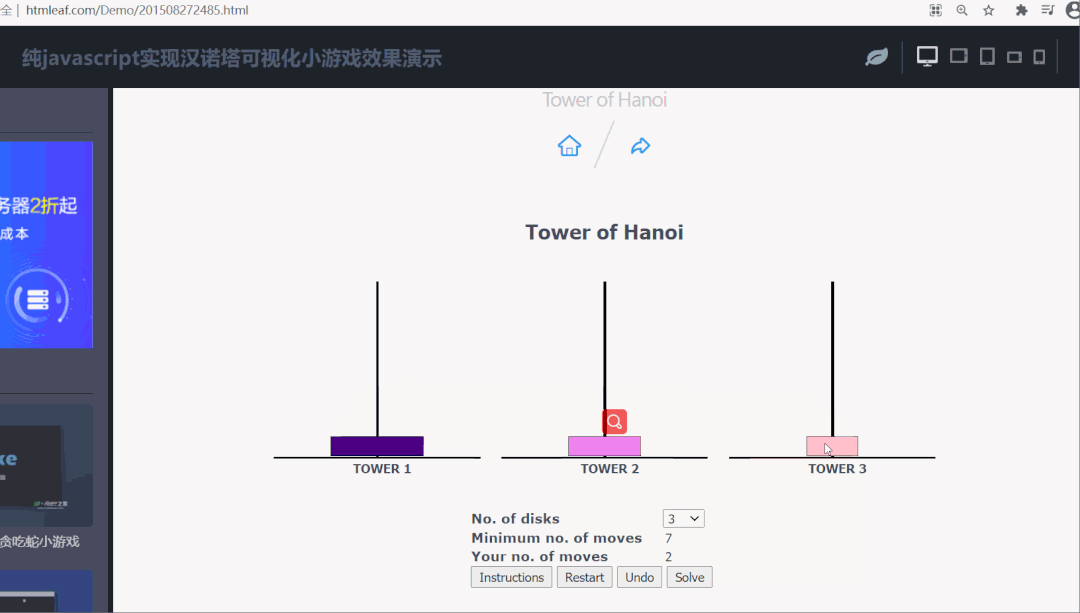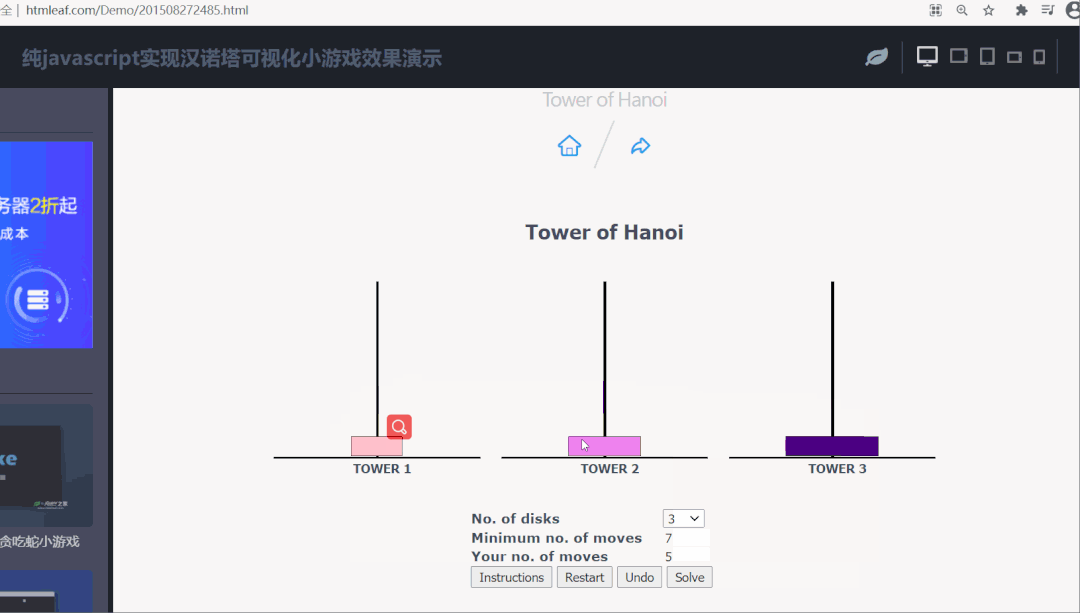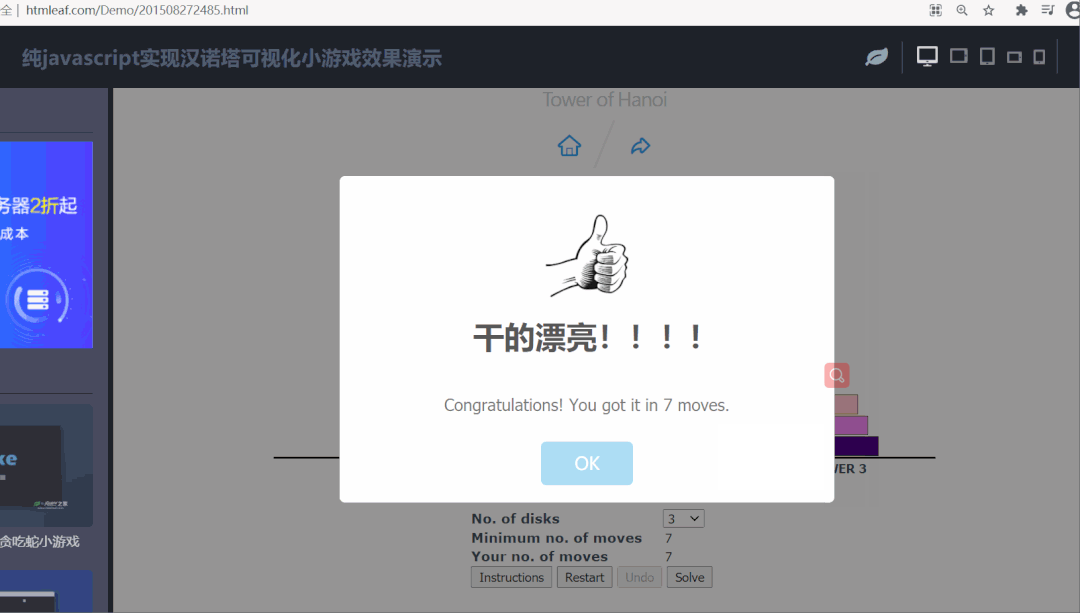
• 将盘片塔从开始柱，经由中间柱，移动到目标柱：首先将上层 N-1个盘片的盘片塔，从开始柱，经由目标柱，移动到中间柱；然后将第N个（最大的）盘片，从开始柱，移动到目标柱。
• 最后将放置在中间柱的 N-1 个盘片的盘片塔，经由开始柱，移动到目标柱。基本结束条件，也就是最小规模问题变为：1个盘片的移动问题。

def move_tower(height, start_pole, mid_pole, target_pole):
    if height >= 1:
        # 开始柱  目标柱  中间柱
        move_tower(height - 1, start_pole, target_pole, mid_pole)
        # 记录移动
        move_disk(height, start_pole, target_pole)
        # 中间柱  开始柱  目标柱
        move_tower(height - 1, mid_pole, start_pole, target_pole)




    
def move_disk(disk, start_pole, target_pole):
    print(f"将 {disk} 号盘子从 {start_pole}号柱 移到 {target_pole}号柱")

move_tower(3, "1", "2", "3")    # 2^n - 1次
print("Complete!")

结果如下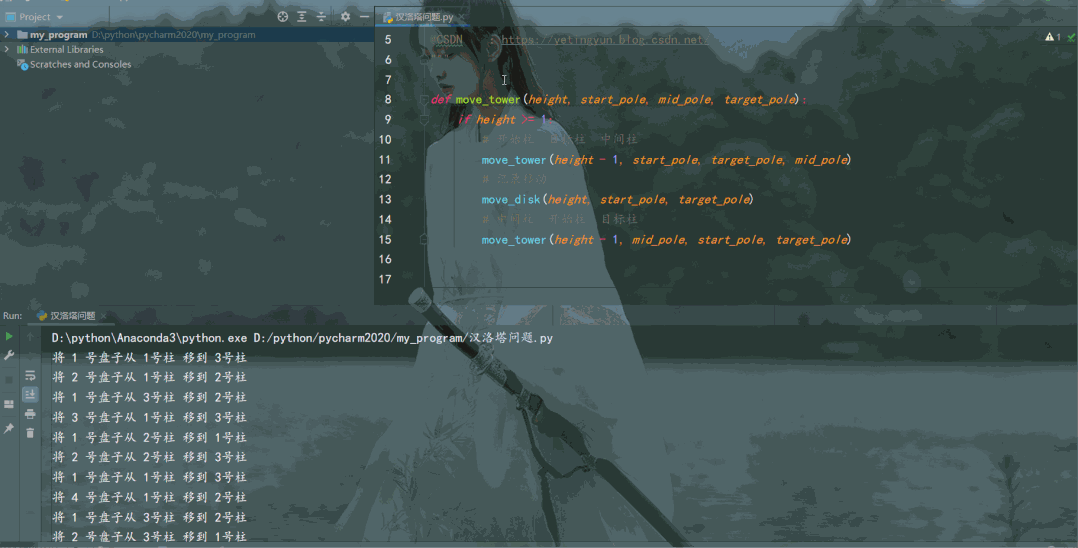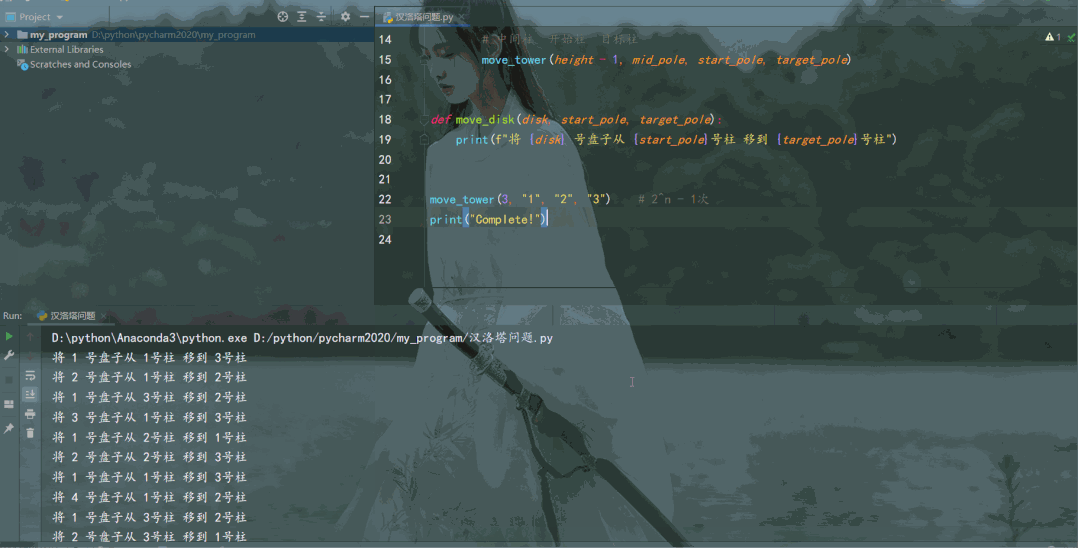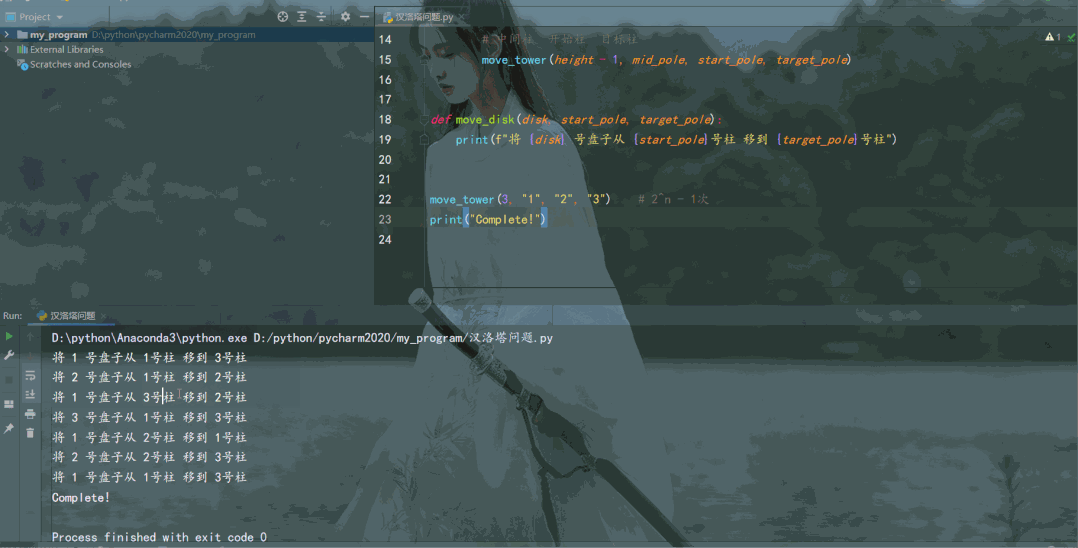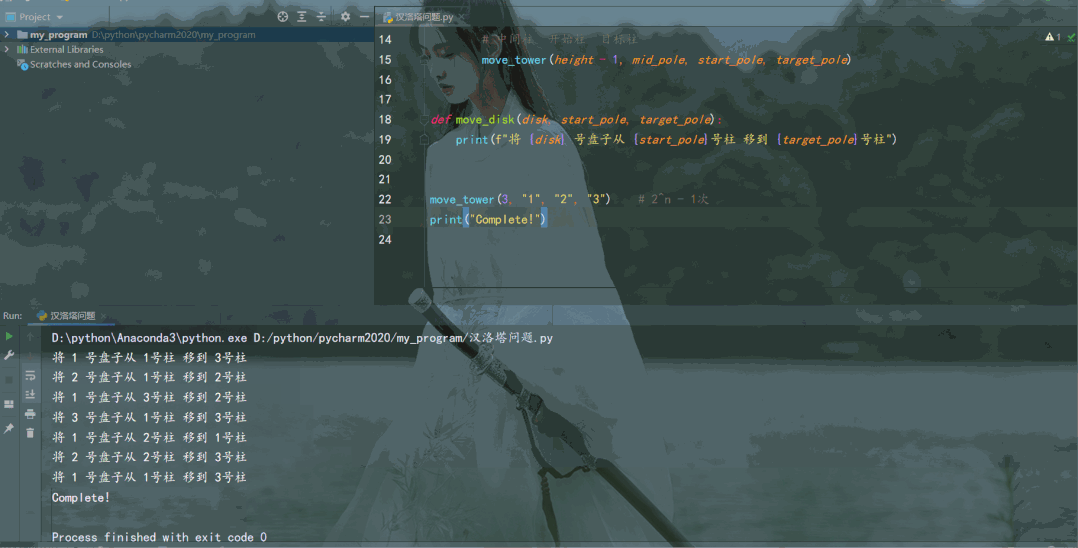：和动图里我们玩游戏的操作步骤一致！

五、总结

递归是解决某些具有自相似性的复杂问题的有效方法

• 递归算法必须要有结束条件（最小规模问题的直接解决）
• 递归算法必须能改变状态向基本结束条件演进（减小问题规模）
• 递归算法必须调用自身（解决减小了规模的相同问题）

• 某些情况下，递归可以代替迭代循环，递归算法通常能够跟问题的表达自然契合。
• 递归不总是最合适的算法，有时候递归算法会引发巨量的重复计算，"记忆化/函数值缓存"可以通过附加存储空间记录中间计算结果来有效减少重复计算（备忘录技术）。
• 如果一个问题最优解包括规模更小相同问题的最优解，这时我们可以用动态规划来解决。