假设检验与 Python 实践

文/小文的数据之旅图片来源于网络

假设检验就是利用小概率事件原理（发生概率很小的随机事件在一次试验中几乎不可能发生）判断是否可以拒绝原假设的一个工具。

在生活中的应用假设检验的例子有很多，最常见的就是在法庭上，法官先假设嫌疑犯无罪，然后收集证据，如果有足够证据证明嫌疑犯有罪，则拒绝原假设，宣判嫌疑犯有罪。假设检验做的就是这么一回事，它之所以重要是因为它是我们思考问题，分析问题，解决问题的一套逻辑思维方法论。

假设检验的步骤

（1）提出原假设（H0）与备选假设（H1）

原假设往往与备选假设是互斥的，即当我们拒绝原假设时，必然会接受备选假设

（2）选择合适的检验统计量

常用的检验统计量：z统计量、t统计量和统计量。z统计量和t统计量常用于均值和比例的检验，统计量则用于方差的检验。
检验统计量的选择往往与样本量n的大小以及是否已知总体标准差σ有关。当总体服从正态分布，样本量n大于30时，无论是否已知总体标准差，都使用z统计量；当n小于30时，若总体标准差已知，则使用z统计量，若总体标准差未知，样本标准差已知，则使用t统计量。
这里大家可能会有疑问，为什么样本量大，无论是否已知总体标准差，都使用z统计量？其实很好理解，因为当样本量小时，t统计量与z统计量差异很大，当样本量大时，t统计量与z统计量差异很小，因此即使总体标准差未知，依然可以用z统计量。
计算公式：

（3）确定用于做决策的拒绝域

拒绝域之前，先要定显著性水平α，一般α=0.05或者0.01

（4）求出检验统计量的p值

通过样本的抽样分布计算p值

（5）查看样本结果是否位于拒绝域内

左单侧检验：备选假设包含小于号（α）
右单侧检验：备选假设包含大于号（α）（卡方检验只有右单侧一种）
双侧检验：备选假设包含不等于号（α/2）

（6）作出决策

如果p值位于拒绝域内，则有充足的理由拒绝原假设；
如果p值位于拒绝域外，则不能拒绝原假设；

实战出真理

import numpy as np
import pandas as pd
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

data = pd.read_csv('./desktop/test.csv')
data.info()
out:

RangeIndex: 130 entries, 0 to 129
Data columns (total 3 columns):
Temperature    130 non-null float64
Gender         130 non-null int64
HeartRate      130 non-null int64
dtypes: float64(1), int64(2)

data.describe()
out:
    Temperature      Gender   HeartRate
count   130.000000  130.000000  130.000000
mean     98.249231    1.500000   73.761538
std       0.733183    0.501934    7.062077
min      96.300000    1.000000   57.000000
25%      97.800000    1.000000   69.000000
50%      98.300000    1.500000   74.000000
75%      98.700000    2.000000   79.000000
max     100.800000    2.000000   89.000000

通过data.info()可以看到数据有130行3列，都为数值型数据，且没有空值，然后用data.describe()查看一下数据分布。

>>>>

问题一：人体体温的总体均值是否为98.6华氏度？

答：

原假设H0：人体体温的总体均值等于98.6华氏度
备选假设H1：人体体温的总体均值不等于98.6华氏度

目前已知条件：样本量n=130（大于30），总体标准差未知，样本均值、样本标准差通过计算可知，因此选择使用z统计量进行检验。

def get_result(data,z,u):
'''
data:数据
z：置信水平对应的z值
u：总体均值
'''
    sample_num = len(data)
    sample_mean = data.mean()
    #计算样本标准差时注意一下，pandas的std（）默认的是样本标准差；
    #numpy的std（）默认的是总体标准差，若要求样本标准差，需设置ddof =1
    sample_std = data.std()
    sample_z = np.sqrt(sample_num)*(sample_mean-u)/sample_std
    #当|sample_z|>z,落在拒绝区域，拒绝原假设
    if (sample_z (-1*z)):
        print('不能拒绝原假设')
    else:
        print('拒绝原假设')

get_result(data['Temperature'],1.96,98.6)
out：
拒绝原假设

结果：拒绝原假设，即人体体温的总体均值不等于98.6华氏度。

>>>>

问题二：人体的温度是否服从正态分布？

答：在重温统计学--抽样分布的python实践部分提到可以通过Shapiro-Wilk test、kstest和normaltest检验是否服从正态分布。

ks_test = stats.kstest(data['Temperature'], 'norm')
shapiro_test = stats.shapiro(data['Temperature'])
normaltest_test = stats.normaltest(data['Temperature'],axis=0)
print('ks_test:',ks_test)
print('shapiro_test:',shapiro_test)
print('normaltest_test:',normaltest_test)

out：
ks_test: KstestResult(statistic=1.0, pvalue=0.0)
shapiro_test: (0.9865769743919373, 0.2331680953502655)
normaltest_test: NormaltestResult(statistic=2.703801433319236, pvalue=0.2587479863488212)

结果：p值大于0.05，人体温度服从正态分布。通过概率分布图，可以看出人体体温的分布形状类似正态分布。

sns.distplot(data['Temperature'])

>>>>

问题三：人体体温中存在的异常数据是哪些

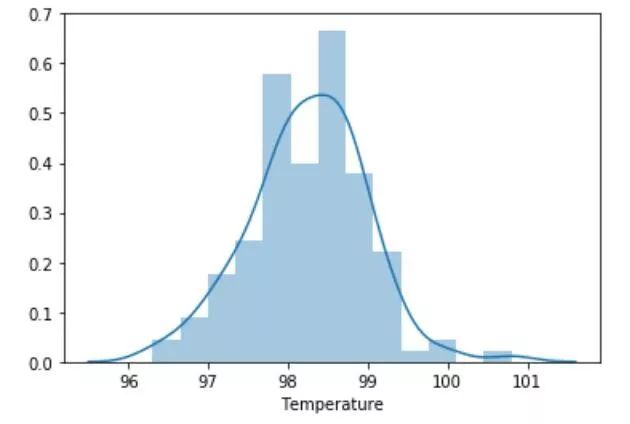
答：因为人体体温样本是服从正态分布的，因此当设定置信水平为95%时，其置信区间为：

sample_mean = data['Temperature'].mean()
sample_std = data['Temperature'].std()
sample_min = sample_mean-1.96*sample_std
sample_max = sample_mean+1.96*sample_std
print('当置信水平为95%时，人体体温样本的置信区间为({},{}).format(sample_min,sample_max)')
out：
当置信水平为95%时，人体体温样本的置信区间为(96.81219177947443,99.6862697589871)

因此，不在置信区间(96.81219177947443,99.6862697589871)范围内的值都可以认为是小概率事件了，即可以认为是异常值。

更为谨慎的，我们可以将置信水平设为99%，即我们常说的正态分布“3σ”原则，求出置信区间。

sample_min = sample_mean-2.58*sample_std
sample_max = sample_mean+2.58*sample_std
print('当置信水平为99%时，人体体温样本的置信区间为({},{}).format(sample_min,sample_max)')
out：
当置信水平为99%时，人体体温样本的置信区间为(96.35761822149028,100.14084331697124)

更为一般的，直接用（μ-3σ,μ+3σ）为置信区间。

>>>>

问题四：男女体温是否存在明显差异？

答：

原假设H0：男女体温不存在明显差异，即男女体温均值差为0
备选假设H1：男女体温存在明显差异，即男女体温均值差不为0

目前已知条件：男样本量n1=65（大于30），女样本量n2 = 65（大于30），总体标准差未知，样本均值、样本标准差通过计算可知，因此选择使用z统计量进行检验。

def get_result_two(data,z):
'''
data:数据
z：置信水平对应的z值
'''
    data_f = data[data.Gender == 2]['Temperature']  #Gender=2，女
    data_m = data[data.Gender == 1]['Temperature']  #Gender=1，男
    sample_num_f = len(data_f)
    sample_mean_f = data_f.mean()
    sample_std_f = data_f.std()
    sample_num_m = len(data_m)
    sample_mean_m = data_m.mean()
    sample_std_m = data_m.std()
    sample_z = (sample_mean_f-sample_mean_m)/np.sqrt(sample_std_f**2/sample_num_f+sample_std_m**2/sample_num_m)
    if (sample_z (-1*z)):
        print('不能拒绝原假设')
    else:
        print('拒绝原假设')

get_result_two(data,1.96)
out：
拒绝原假设

>>>>

问题五：体温与心率间的相关性（强？弱？中等？)

答：数值型的数据一般使用皮尔逊相关系数来衡量其线性相关性。

原假设H0：人体体温与心率不相关，r=0
备选假设H1：人体体温与心率相关，r不等于0

解法1：
def get_r_pvalue(data,t):
    r = data['Temperature'].corr(data['HeartRate'])
    df = len(data)-2
    sample_t = np.abs(r)*np.sqrt(df/(1-r**2))
    if (sample_t < t) and (sample_t > (-1*t)):
         print('不能拒绝原假设')
    else:
        print('拒绝原假设')#自由度为128，置信水平95%所对应的t值为1.980
get_r_pvalue(data,1.980)out:拒绝原假设   
解法2：
corr_v,corr_p = stats.pearsonr(data['Temperature'],data['HeartRate'])
print('体温与心率的皮尔逊相关系数为{}，p值为{}'.format(corr_v,corr_p))

结果：体温与心率的皮尔逊相关系数为0.25366，p值为0.00359。一般我们认为皮尔逊相关系数小于0.3时为弱相关性，又因为p值小于0.05，即原假设体温与心率不相关的发生概率很低，因此我们可以认为体温与心率的相关性是显著的。

▼ 点击成为社区注册会员 喜欢文章，点个在看