本文内容来源于《测绘学报》2024年第12期（审图号 GS京(2024)2592号）

刘瑾,1,2, 季顺平,1

1.武汉大学遥感信息工程学院，湖北　武汉　430079

2.杭州电子科技大学通信工程学院，浙江　杭州　310018

基金项目

 国家自然科学基金(42171430)

作者简介

第一作者：刘瑾（1996—），女，博士，研究方向为多视图立体视觉、影像密集匹配、三维重建。E-mail：liujinwhu@whu.edu.cn

通讯作者: 季顺平　E-mail：jishunping@whu.edu.cn

摘要

近年来，基于深度学习的多视密集匹配方法在三维重建任务上展现出了巨大的潜力，但是这些方法在恢复场景的几何结构细节方面仍显不足。在一些传统的多视密集匹配方法中，法线常被作为一种重要的几何约束来辅助推理精细的深度图，然而，这种蕴含了场景几何结构特征的法线信息在深度学习方法中却并未得到充分利用。本文针对多视密集匹配和三维场景重建任务，提出了一种基于深度学习的深度和法线联合估计方法。该方法采用多阶段金字塔的网络结构，从多视影像中同时推理深度和表面法线，并促进二者的联合优化。所提出的网络由特征提取模块、法线辅助的深度估计模块、深度辅助的法线估计模块及深度-法线联合优化模块组成。其中，深度估计模块通过整合表面法线信息构建具有几何感知的代价体，从而推理精细的深度图；法线估计模块利用深度约束构建局部代价体来推理精细的法线信息；联合优化模块则用于增强深度和法线估计结果之间的几何一致性。在WHU-OMVS数据集上的试验结果表明，本文方法在深度推理和表面法线推理任务上都表现出色，并显著优于现有方法。在两种不同数据集上的三维重建结果进一步表明，本文方法能够有效地恢复局部高曲率区域和全局平面区域的几何结构，有助于获得具有良好结构的高质量三维场景模型。

关键词

深度估计; 法线估计; 多视密集匹配; 深度学习; 三维重建

本文引用格式

刘瑾, 季顺平. 深度和法线联合估计的深度学习多视密集匹配方法[J]. 测绘学报, 2024, 53(12): 2391-2403 doi:10.11947/j.AGCS.2024.20230579

LIU Jin, JI Shunping. Deep learning based multi-view dense matching with joint depth and surface normal estimation[J]. Acta Geodaetica et Cartographica Sinica, 2024, 53(12): 2391-2403 doi:10.11947/j.AGCS.2024.20230579

阅读全文

http://xb.chinasmp.com/article/2024/1001-1595/1001-1595-2024-12-2391.shtml

从多视遥感影像重建地表三维场景在数字城市构建、自然灾害监测和评估、工程测量、古文物遗迹保护和存档等诸多领域中发挥着至关重要的作用[1-2]。影像密集匹配是三维重建的核心技术。近年来，以深度学习为代表的人工智能技术逐渐占领了诸多研究领域，对计算机视觉、遥感图像处理中的相关技术形成了冲击和促进[3-6]。在这种趋势下，基于深度学习的影像密集匹配方法也受到了广泛研究，并且相较于传统密集匹配方法也显示了一定的优越性[7-11]。在多视立体匹配任务上，MVS-Net[12]率先将多视几何嵌入深度学习网络模型中，通过特征提取、代价体构建、代价体规则化和深度回归等过程，实现了端到端的深度图估计。Cas-MVSNet[13]则进一步在MVS-Net的基础上构建了多级金字塔结构，利用粗分辨率的推理结果来约束高分辨率阶段的深度搜索范围，实现由粗到精的匹配，从而减少时间和显存开销。这类典型的深度学习多视密集匹配方法，在各类开源数据集上表现出了良好的性能，并启发了一系列的后续研究[14-17]。在针对城市级别的三维模型重建任务上，也出现一些专用于遥感影像的深度学习多视密集匹配方法。例如MS-REDNet[18]设计了基于循环卷积编码-解码结构的代价聚合模块，极大降低了网络的显存占用，使其更适合处理具有大幅面、宽深度搜索范围的航空影像；Ada-MVS[19]则考虑了多视影像的可视性关系，以逐视角的可视性为权重，自适应融合多视匹配代价体，从而更好地应对倾斜多视航空影像中的几何变形和视角遮挡现象；Sat-MVS[20-21]实现了一种基于有理多项式模型的高维特征变形模块，成功地将深度学习方法用到了多视卫星影像密集匹配任务上。

尽管这些方法在整体的深度估计上取得了良好的效果，但在推理边缘、角点和平面等结构区域的精细度和真实性方面仍存在挑战。究其原因，一方面，这些方法在构建多视影像代价体时，仅考虑了多视图之间的几何约束，却忽略了单个视图内相邻像素之间的几何结构关系；另一方面，这些基于学习的方法通过最小化所有像素的深度差异的总和来训练网络，并不专门惩罚相邻像素之间的几何不一致现象。对几何约束的考虑不足，则导致在一些结构化区域出现重建失真现象，如在高曲率区域丢失局部细节，或在平坦区域产生凹凸不平表面。

场景的表面法线信息可以直观地展示结构区域的几何特征。一些传统的多视匹配方法将深度估计任务与表面法线结合，以增强重建结果的几何一致性[22-25]。文献[22]在基于Patch Match策略的匹配流程中，将逐像素的深度初始化和传播与其法线信息结合起来，以恢复高质量的倾斜表面和深度细节；COLMAP[24]遵循倾斜平面假设，整体考虑深度、法线和逐像素的视角选择，并同时对这些变量进行视图间的传播和迭代求解。然而，这个在传统方法中被广泛使用的重要几何信息，在基于深度学习的匹配方法中却没有被充分利用。少数的方法要么仅将表面法线作为一种先验信息来改善深度估计的性能[26]，或者使用两个独立的分支分别估计深度和法线，而不考虑二者之间的几何一致性[27]，或者经验性的设计后处理工具以优化深度结果[28]，这些方法在设计和性能上都具有一定的局限性。

为了提升现有深度学习方法重建结果的精细度和几何结构的一致性，本文设计了一种新颖的、基于深度学习的深度和法线联合估计方法，用于多视密集匹配和三维场景重建任务。该方法将深度和表面法线之间紧密的几何关系纳入基于学习的网络中：在初始深度的约束下推理精细的表面法线，并在初始法线的引导下推理精细的深度图。整个网络采用多阶段金字塔的结构进行由粗到精的推理。在金字塔顶层，先推理出初始的粗糙深度图，然后以初始深度图为约束，在缩小的深度搜索范围内构建局部代价体用于推理初始表面法线；在高分辨率阶段，将初始表面法线信息纳入局部代价体中，构建具有几何信息的新代价体，用于更精细的深度推理，随后用推理出的深度图进一步约束代价体的构建用于推理更精细的法线图。此外，在每个阶段，设计了一个深度-法线优化模块，进一步增强深度和法线推理结果的几何一致性。通过将深度和法线之间的几何约束显式地纳入深度学习多视密匹配网络中，从而实现细粒度的三维场景重建。

1　方法

本文提出了一种联合深度和法线估计的多视密集匹配网络（joint depth and normal estimation multi-view dense matching network，DN-MVS），该方法以现有的深度学习多视密集匹配网络Cas-MVSNet[13]作为基准模型，在基准模型上改进了一种法线辅助的深度估计模块，并新增了深度辅助的法线估计模块以及深度法线联合优化模块，从而提升基准模型匹配和重建结果的结构精细度。该方法的整体结构如图1所示，其中，特征提取模块从多视影像中提取3个尺度的特征图，对应金字塔的3个推理阶段；深度估计模块在金字塔第一阶段，从多视全局代价体中推理初始深度图，在后续阶段通过集成法线信息构建几何感知的局部代价体，以推理具有精细结构的深度图；表面法线估计模块则在初始深度的约束下构建局部代价体，从而推理精细的法线图；深度法线联合优化模块则通过学习的方式共同提升二者的几何结构质量。最后使用深度和法线组合的多测度损失对网络进行端到端的训练。

图1

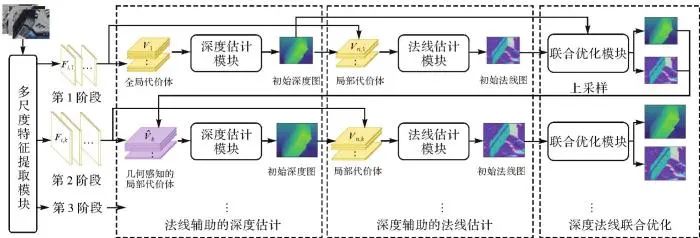
图1   本文提出的联合深度和法线估计的多视密集匹配网络（DN-MVS）

Fig. 1   The proposed join depth and normal estimation multi-view dense matching network (DN-MVS)

1.1　多尺度特征提取

本文采用与文献[13,16]相似的编码器-解码器结构，从多视影像中提取多个尺度的高维特征表示。该编码器-解码器结构包含3个尺度的2D卷积和2D上卷积层，在每个尺度的卷积层和上卷积层之间具有一个跳跃连接。对于每个输入图像，提取了3个尺度的特征图，其大小分别是原始输入影像大小的{1/16，1/4，1}，通道数分别为32、16和8。

1.2　法线辅助的深度估计

DN-MVS网络的深度推理模块是在其基准网络[13]上进行的改进：在更精细的金字塔阶段上，将推理的表面法线集成到当前阶段的局部代价体中，以构建具有几何感知的代价体，从而推理具有精细结构的深度图。本节先简要回顾基准网络中常规的深度推理过程，然后重点介绍改进的具有几何感知的代价体构建策略。

在基准网络中，深度估计在金字塔3个阶段上依次进行，如图2（a）所示。在第一阶段，在整个深度搜索空间内构建全局代价体以估计初始的粗糙深度图。在后续阶段，利用初始深度约束构建局部代价体以进行高分辨率的深度推理。具体来说，在第k阶段，给定参考相机视锥体中的一个假想深度平面d，通过可微分的单应映射变换[12]，将每个邻域特征图映射到参考影像视角下，实现多视特征的对齐。随后，将对齐的N个视角的特征图聚合成一个代价图C。对于dk个深度采样平面，可以得到代价图集合，这些代价图堆叠为一个代价体Vk。随后利用3D卷积结构对代价体进行规则化，并通过概率加权求和的方式回归当前阶段的深度图。在由粗到细的推理中，每个阶段的深度平面均在当前阶段的深度搜索范围内进行均匀采样。其中，第一阶段的深度搜索范围覆盖整个研究区域的地表起伏变化范围，后续阶段的深度搜索范围缩小为以上一阶段推理的深度图为中心的局部缓冲区。

图2

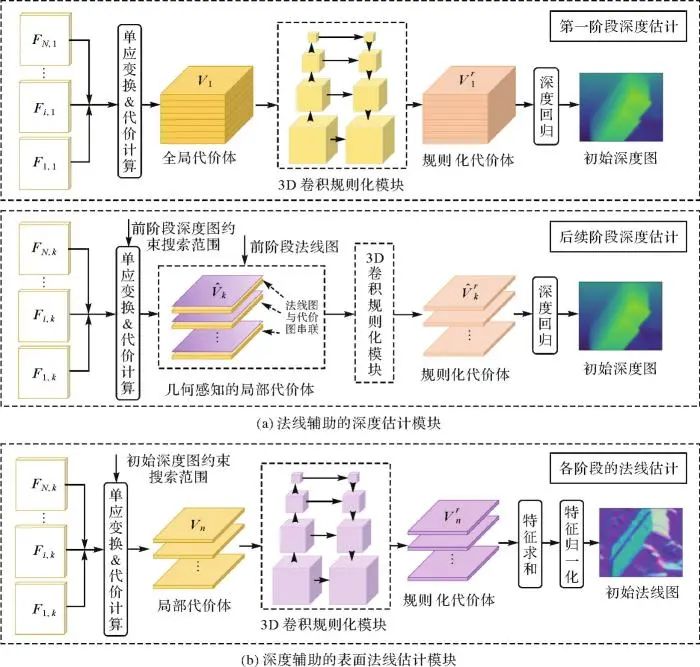
图2   金字塔3个阶段的深度估计模块和法线估计模块结构

Fig. 2   The structure of depth estimation module and normal estimation module at three pyramid stages

构建良好的代价体有助于后续推理出优质的深度图。先前的工作[13,21,16]在构建代价体时仅考虑多视影像之间的几何约束关系，忽略了同一个影像内相邻像素之间的几何关系。由于相邻像素之间缺乏有效的几何约束，推理的深度图可能在结构化区域出现失真现象，如在高曲率区域丢失细节或在平面区域中产生颠簸。而法线信息可以为影像各部分的几何结构提供重要线索，因此，本文在常规深度推理过程中，引入了一种简单有效的策略，即将表面法线整合到基础多视代价体中，形成一个具有几何结构感知的新代价体用于精细的深度推理。

在具体实现中，DN-MVS在基准模型的第k阶段（k≥2）上构建几何感知代价体，如图2（a）所示。首先，对前一阶段估计的表面法线图进行上采样，然后，将上采样后的法线图与第d个深度平面上的代价图Ck,d进行串联，得到一个新的集成了法线信息的代价图。对于dk个代价图，可以得到集合，这些新代价图被堆叠为一个新的代价体。在每个阶段，采用与[13]相同的3D U-Net结构对经过良好构建的代价体进行规则化。利用softmax操作将规则化后的代价体转为概率体P，将所有深度假设的归一化概率加权和作为最终的推理深度图Dk。通过将表面法线信息显示地融入代价体中，深度推理可以与局部几何约束相关联，这有助于生成具有清晰边界和一致结构的精细深度图。

1.3　深度辅助的表面法线估计

与深度推理一致，法线推理也在金字塔3个阶段上由粗到细地进行。与从全局代价体中独立推理法线图的方法[27-28]不同，DN-MVS选择从初始深度约束的局部代价体中推理法线图。这是因为，一方面初始深度图已经提供了潜在的地物表面位置，这意味着在缓冲区之外的部分可被视为无效区域而无须遍历；另一方面，法线代表的是局部特征属性，因此根据局部邻域特征空间便可推理出合理的法线结果。

在金字塔第k阶段（k=1，2，3），利用初始深度图约束，从多视角特征中构建局部代价体用于推理初始表面法线图，其过程如图2（b）所示。用于法线推理的局部代价体是在局部深度搜索范围内构建的，该范围是以当前阶段推理的初始深度图Dk为中心，向外扩展的深度缓冲区。在这个局部搜索范围内以Sm为间隔均匀采样dm个假想深度平面。然后，与深度推理模块中的代价体构建过程类似，在每个深度采样平面上，通过单应映射变换操作将所有邻域特征图在参考影像视角下对齐，并聚合成用于推理法线的局部代价图。对于dm个代价图，堆叠为一个形状为C×dm×H×W的代价体Vn,k，其中C为特征通道数，H和W分别为当前阶段特征图的高和宽。接着，利用代价体规则化模块进一步处理Vn,k，得到大小为3×dm×H×W的规则化代价体。代价体规则化模块是一个具有4个尺度的3D U-Net结构，除最后一层外，其余每个3D卷积和上卷积层后面都跟着一个批归一化层和修正线性单元。最后，沿着深度维度对求和，并沿着特征通道维度对求和后的进行归一化，最终输出当前阶段的初始法线图Nk。

1.4　深度-法线联合优化

基于深度和法线之间紧密的几何相关性，本文设计了可学习的深度-法线联合优化模块，以提高初始推理结果的几何质量。联合优化模块被设置在每个金字塔层的深度推理和法线推理模块之后。它借助初始的深度图Dk优化初始法线图Nk，并在初始法线图Nk和影像信息的指导下优化初始深度图Dk，如图3所示。

图3

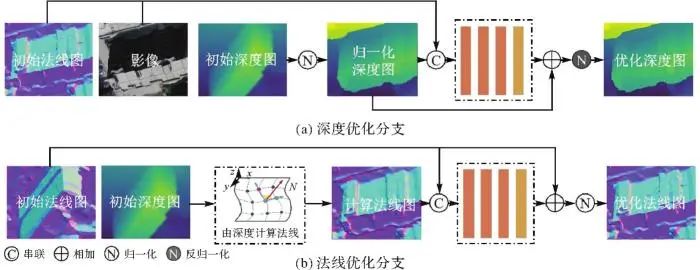
图3   深度-法线联合优化模块结构

Fig. 3   The structure of depth-normal join optimization module

在深度优化分支中，初始深度图首先被归一化到[0，1]之间。然后，将归一化的深度图、初始法线图和经过尺寸调整的参考影像串联起来。接着，通过一个由4个2D卷积层构成的可学习模块从串联后的图像中学习深度残差。这里，每个卷积层的卷积核大小为3×3，通道数为32，前3个卷积层后具有一个整流线性单元层。最后，将深度残差与归一化的深度图相加，通过反归一化操作得到优化后的深度图。

在法线优化分支中，首先从初始深度图中计算出一个新的表面法线图，表示为。这里采用文献[29]方法，选取8对相邻像素分别计算中心点的法线向量，最终的法线方向表示为这8个法线向量的平均值。将与初始法线图Nk串联起来，形成一个6通道的输入。然后采用4个2D卷积层从这个6通道特征图中学习法线残差。每个卷积层的卷积核大小为3×3，通道数为32，前3个卷积层后具有一个整流线性单元层。将学习到的残差与初始法线Nk相加，得到优化后的法线图。

1.5　损失函数

用于训练网络的损失函数由真值标签和推理结果之间的Smooth L1 Loss表示

(1)

式中，x和y分别表示推理值和标签值。

总损失由多种测度构成，包括：深度损失项、法线损失项、深度-法线约束项，以及几何一致项。其中，深度损失项和法线损失项分别表示为

(2)

(3)

式中，D、Dr和Dgt分别表示初始深度、优化深度、以及真值深度；N，Nr和Ngt分别表示初始法线、优化法线、以及真值法线；M是所有有效像素的集合。

深度-法线约束项用于对深度推理施加额外的几何约束。这里将从初始深度中计算出的表面法线图表示为Nd2n，通过强制执行Nd2n与真值法线Ngt之间的一致性，将深度估计与表面法线的几何约束相关联

(4)

此外，本文还使用了几何一致性损失项来约束推理深度和推理法线结果间的一致性，定义为

(5)

金字塔第k阶段的总损失表示为

(6)

在试验中，各损失项的权重参数{α1，α2，β}被经验性地设置为{3，2，3}。

整个网络的总损失表示为所有阶段损失值的加权和

(7)

每个阶段的权重参数{λ1，λ2，λ3}分别设置为{0.5，1，2}，即高分辨率阶段的结果所占权重更大。

2　试验结果与分析

本文在开源的模拟倾斜多视航空数据集WHU-OMVS[19]上评估所提方法的深度估计精度、法线估计精度，以及在物方的三维模型重建质量。并在一套真实拍摄的天津地区倾斜多视无人机影像上进行迁移应用，以评估所提方法在真实场景下的重建应用能力。

2.1　实现细节

所提出的联合深度与法线估计网络在Py Torch 1.8.0框架下实现。该网络采用三阶段的金字塔结构，每个阶段提取的特征图的空间分辨率分别为原始图像大小的{1/16，1/4，1}。深度估计模块的深度采样平面数量设定为{48，32，8}，深度采样间隔设置为{（dmax-dmin）/48 m，0.2 m，0.1 m}，其中dmax和dmin分别是深度搜索范围的上界和下界，这是从Sf M的稀疏场景点云中获得的。在表面法线估计模块中，3个阶段的深度采样平面数量分别为{8，8，8}，深度采样间隔设置为{0.4 m，0.2 m，0.1 m}。在WHU-OMVS数据集上训练时，一次匹配时输入的影像视角数量为5，选择RMSProp作为优化器，学习率设置为0.001，训练批次为1，总计进行了约24个周期的迭代训练。将预训练后的模型嵌入端到端的三维重建管道[19]中应用，匹配的视图数量设置为N=5，一致性检验阈值设置为Nc=10和Nf=3。所有方法都在硬件环境为NVIDIA TITAN RTX GPU（24 GB）和Intel i9-9900X CPU@3.60 GHz上进行密集匹配和三维重建评估。在试验中，所有重建方案采用相同的相机内外方位参数作为输入，这些参数是由数据集提供的，具有良好的精度。

2.2　评价指标

本文在深度推理结果、法线推理结果及重建的数字表面模型（digital surface model，DSM）结果上进行定量精度评定。

对于深度推理结果，采用的评价指标如下。

（1）平均绝对误差（mean absolute error，MAE），即估计深度值与地面真实深度值之间绝对误差的平均值，表示为

(8)

式中，和分别表示第i个像素上的估计深度值与真实深度值；n表示有效像素总数量。这里仅统计绝对差小于100个深度间隔的像素，以消除极大异常值对均值统计的影响。

（2）准确率百分比（percentage of accurate grids，PAG-Dα），即绝对差小于深度阈值α的像素个数占所有像素数量的百分比

(9)

式中，m指真值深度图中的有效像素个数；mα指估计深度图与真值深度图的绝对深度误差小于阈值α的像素个数。在试验中α分别取值为0.1、0.3和0.6 m。

对于表面法线结果，利用推理法线向量与地面真实法线向量之间的角度误差来衡量估计值的质量

(10)

式中，和分别表示第i个像素点的推理法线向量和真实法线向量。以所有有效像素的估计法线与真值法线之间夹角误差的平均值（mean）和中位数（median）作为评价指标。此外，还统计了绝对角度误差小于阈值β的像素准确率百分比（PAG-Nβ），其定义与式（9）类似，其中β分别取值10°、20°和30°。

对于重建的DSM结果，本文遵循之前的研究工作[19]，统计DSM的网格准确率百分比（PAG-Sγ），其定义与式（9）类似，这里不再赘述，其中γ取值0.2、0.4和0.6 m。

2.3　在WHU-OMVS数据集上的试验与对比

WHU-OMVS数据集[19]是一个大规模的合成多视倾斜航空影像数据集。训练集包括了由五视倾斜相机拍摄的约3万张的影像，大小为768×384像素，附带有地面真值深度图、真值表面法线图和成像参数。模拟飞行高度约为220 m，下视影像对应的地面采样间距约为0.1 m。测试集有切片小图和大图两个版本，对应的是相同的测试区域。其中，切片小图版本具有4715张768×384像素大小的倾斜五视影像，以深度图和表面法线图作为真值标签；大图版本包括268张大小为3712×5504像素的影像，覆盖地表场景范围约为850×700 m2，对应地面分辨率为0.1 m。并提供了DSM作为物方真值，以便于在物体空间中对3D重建结果进行评估。本节在切片小图上评估深度图和法线图结果，在测试集大图上评估DSM的精度。

2.3.1　深度结果评估

为了说明本文方法在深度估计任务上的性能，选取了3种最相关的方法作为对比。其中，COLMAP[24]是基于Patch Match匹配策略[22]发展而来的传统的三维重建方法，通过求解概率图模型来联合推理深度和表面法线；NAS[27]是一种用于联合估计深度和法线的深度学习密集匹配方法，该方法采用的是单阶段的推理结构，因此将深度采样平面数量设为192，采样间隔设为（dmax-dmin）/192 m；而Cas-MVSNet是3阶段的深度学习密集匹配网络，采用与本文方法完全相同的超参数设置以及训练和推理策略。3种深度学习方法都在WHU-OMVS训练集上训练，在切片测试集的深度图上进行精度评估，结果见表1。

表1   4种方法在WHU-OMVS测试集上的深度估计精度

Tab. 1  The accuracy of depth estimation by four methods on the WHU-OMVS patch-size test set

方法	MAE/m↓	PAG-D0.1 m/（%）↑	PAG-D0.3 m/（%）↑	PAG-D0.6 m/（%）↑
COLMAP	0.279	48.40	75.60	88.00
NAS	0.289	31.82	71.58	90.32
Cas-MVSNet	0.157	60.14	92.00	96.87
DN-MVS（本文方法）	0.132	61.89	93.09	97.81

新窗口打开| 下载CSV

由表1可以看出，与同样执行深度和法线联合估计任务的COLMAP和NAS方法相比，本文的DN-MVS方法在所有指标上都表现出了显著的优越性。具体来说，DN-MVS在MAE指标上相比传统方法COLMAP改进了52.68%，相比基于学习的NAS方法改进了54.33%。进一步的，在具有最严格阈值的PAG-D0.1 m指标上，所提出的方法相比于COLMAP和NAS分别提升了13.49%和30.07%，这显示了DN-MVS估计的深度结果具有良好的精细度。与Cas-MVSNet相比，DN-MVS在各个测度上都具有明显的改进。从数值上来看，相比于Cas-MVSNet，DN-MVS的MAE指标从0.157 m降低到0.132 m，提升幅度为15.92%，而绝对差小于0.1、0.3和0.6 m的像素百分比分别为61.89%、93.09%和97.81%，相比于Cas-MVSNet分别提升了1.75%、1.09%和0.94%。这种改进主要来自本文构建的具有几何感知的代价体结构，此外，深度和法线的联合优化也有助于更好的预测。图4展示了在WHU-OMVS测试集上不同方法产生的深度图、以及局部区域的放大可视化效果。从放大图中可以看出，本文方法相比于其他3种方法，能够产生更加清晰和锐利的地物边界，其效果更接近真值深度图的形状，而Cas-MVSNet方法的结果较为模糊，COLMAP则具有较多的误匹配区域，地物边界变形严重，NAS方法在地物边界处的深度结果则过于平滑。

图4

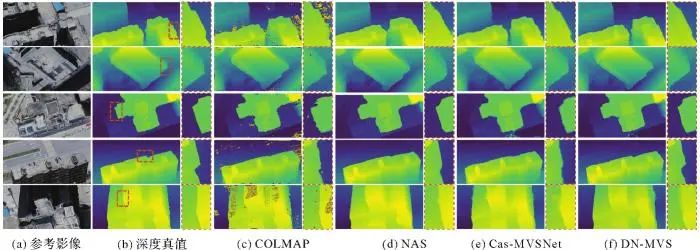
图4   在WHU-OMVS测试集中5个不同视角影像上的深度估计图及局部放大效果

Fig. 4   The depth estimation results and localized enlargements of five view images in WHU-OMVS test set

2.3.2　表面法线结果评估

本节统计不同方法推理的表面法线结果，参与评估的方法与3.3.1节保持一致。涉及的深度学习方法在WHU-OMVS训练集上训练，在切片测试集的表面法线真值图上进行精度评估。值得注意的是，Cas-MVSNet是专用于深度估计的深度学习方法，自身没有法线推理功能，因此这里直接从估计的深度图中计算表面法线用于评估，而对于其他3种方法，直接评估推理出的法线图。各种方法的法线定量结果见表2。

表2   4种方法在WHU-OMVS测试集上的法线估计精度

Tab. 2  The accuracy of surface normal estimation by four methods on the WHU-OMVS patch-size test set

方法	mean/（°）↓	median/（°）↓	PAG-N10°/（%）↑	PAG-N20°/（%）↑	PAG-N30°/（%）↑
COLMAP	20.06	11.54	46.27	68.41	79.28
NAS	16.84	14.20	30.03	70.29	88.61
Cas-MVSNet（D2N）	11.86	7.88	61.91	85.69	93.03
DN-MVS（本文方法）	8.23	5.70	72.20	91.86	97.19

新窗口打开| 下载CSV

由表2可以看出，与Cas-MVSNet从深度图中计算出的法线相比，DN-MVS在所有指标上都具有明显的提升，这显示了本文方法在表面法线估计任务上的有效性。在角度误差的均值上，DN-MVS相比Cas-MVSNet降低了30.6%，相比COLMAP和NAS分别降低了59.0%和51.1%。而在所有百分比指标上，DN-MVS相比于其他方法均具有显著的提升。图5展示了4种方法得到的法线图及局部区域的放大结果。Cas-MVSNet的法线图在建筑物边界处具有较多的误差，在平面区域处产生了颠簸不平现象，NAS方法的法线图则存在较为严重的模糊和失真，COLMAP则具有较多的噪声和误匹配现象。相比之下，DN-MVS估计的法线图在边缘区域更加清晰，在平坦区域更加平滑，其效果最接近真值法线图。

图5

图5   在WHU-OMVS测试集中5个不同视角影像上的法线估计图及局部放大效果

Fig. 5   The normal estimation results and localized enlargements of five view images in WHU-OMVS test set

2.3.3　DSM结果评估

本文借助文献[19]提出的深度学习三维重建框架Deep3D生成测试区的DSM结果。由于Deep3D采用了模块化的结构，因此本文提出的DN-MVS模型可以方便地集成到该框架中进行多视密集匹配，而其他模块和具体参数与其原文中的设置保持一致。除了Cas MVSNet外，本节选取了COLMAP和Open MVS两个开源三维重建方案进行对比。由于COLMAP和Open MVS对内存资源需求过高，影像在被输入各个方案前被统一下采样两倍，随后在重建方案内部禁用所有下采样功能，以消除数据尺度不一致造成的重建质量差异。

鉴于本文更加关注各类方法在恢复地物几何结构方面的有效性，除了整体的定量评估外，本节还对DSM结果的边缘和非边缘区域分别进行了评估，结果见表3。对于具有显著高程变化的地物边缘区域，百分比阈值分别设为{0.2 m，0.4 m，0.6 m}，而对于较为平坦的非边缘区域，采用更加严格的百分比阈值{0.05 m，0.1 m，0.2 m}来展示在平面区域的重建质量。由表3可以看出，在边缘区域，DN-MVS在PAG-S0.2 m指标上相比Cas-MVSNet提升了10.44%，这表明本文方法显著提高了物体边界处的模型重建质量。在非边缘区域，DN-MVS在具有最严格阈值的指标上也具有明显的提升，表明其在平面区域重建的表面更加精确。而完整区域的定量结果显示了本文方法的优越性。图6展示了Cas-MVSNet和DN-MVS生成的实景三维模型和DSM结果的对比图。本文方法重建的模型具有更加规则和平整的平面，在地物边缘处具有较少的噪声和清晰的细节。

表3   4种方法在WHU-OMVS测试集上重建DSM结果评估

Tab. 3  Evaluation of DSM results reconstructed by four solutions on the WHU-OMVS test set

方法	边缘区域			非边缘区域			完整区域
	PAG-S0.2 m/（%）↑	PAG-S0.4 m/（%）↑	PAG-S0.6 m/（%）↑	PAG-S0.05 m/（%）↑	PAG-S0.1 m/（%）↑	PAG-S0.2 m/（%）↑	PAG-S0.2 m/（%）↑	PAG-S0.4 m/（%）↑	PAG-S0.6 m/（%）↑
COLMAP	50.08	71.55	78.01	47.70	65.80	82.74	80.32	92.38	95.67
Open MVS	61.96	78.37	83.35	42.66	64.71	84.94	83.24	94.07	96.53
Cas-MVSNet	50.61	71.30	81.27	44.68	69.90	87.57	84.84	94.40	97.02
DN-MVS	61.05	79.20	84.99	50.99	73.23	88.81	86.76	95.11	97.11
（本文方法）	（+10.44）	（+7.90）	（+3.72）	（+6.31）	（+3.33）	（+1.24）	（+1.92）	（+0.71）	（+0.09）

注：括号内数值表示DN-MVS方法相对于Cas-MVSNet方法的数值提升。

新窗口打开| 下载CSV

图6

图6   Cas-MVSNet和DN-MVS（本文方法）重建的实景三维模型和DSM结果以及二者的放大区域

Fig. 6   The 3D textured mesh and DSM results with the enlarge part produced by Cas-MVSNet and DN-MVS (the proposed method)

2.4　在天津倾斜多视航空影像上的试验结果

为了说明本文方法的泛化能力，本节在一套真实场景中采集的倾斜无人机影像数据上进行迁移应用。测试区域位于天津市郊区，包含342张由五视倾斜相机拍摄的航空影像，覆盖400×350 m2的区域。利用Context Capture软件提前进行了空中三角测量和影像畸变校正。由于地面真值为同一区域的激光点云数据，本节统计不同方法重建的3D点云精度。参考先前的研究工作，本节统计3D点云的平均距离测度和百分比测度[30-31]。对于每种测度，计算点云的准确性（Acc.）和完整性（Comp.）指标，此外，用overall表示准确性和完整性的平均值，用F1值表示准确性和完整性的调和平均值。Cas-MVSNet和DN-MVS使用在WHU-OMVS上得到的预训练模型进行深度推理，而不再进行任何微调，参与匹配的视角数量设置为5。

如表4所示，在WHU-OMVS数据集上预训练的DN-MVS模型在所有指标上都取得了最优的结果。尤其是在综合指标overall和F1值上，DN-MVS相比于其他3种模型都具有明显的提升。可以得知，本文方法表现出了良好的泛化性，即在模拟数据上预训练的模型，在未经任何针对特定场景的微调和优化的情况下，直接应用于之前未见过的真实场景影像，也能获得远优于传统重建方法的精度。这说明深度学习模型学到的底层知识是通用的，不局限于某个特定的目标场景，这一特性对于实际应用来说至关重要。图7展示了4个解决方案重建的实景三维模型和DSM结果。虽然所有解决方案都重建出了结构良好的3D模型，但本文的DN-MVS在平面区域表现出更平滑的外观，并且噪声更少。

表4   在天津测试区的3D点云重建结果评估

Tab. 4  Evaluation of 3D point cloud results in the Tianjin test area

方法	平均距离/m↓			百分比（阈值<0.2 m）/（%）↑			百分比（阈值<0.4 m/（%））↑
	Acc.	Comp.	overall	Acc.	Comp.	F1值	Acc.	Comp.	F1值
COLMAP	0.509	0.367	0.438	46.14	62.91	53.24	66.10	81.96	73.18
Open MVS	0.410	0.306	0.358	47.57	72.97	57.59	75.03	84.61	79.53
Cas-MVSNet	0.410	0.256	0.333	51.41	80.13	62.63	74.82	87.10	80.49
DN-MVS	0.404	0.237	0.320	51.51	81.53	63.13	75.28	87.86	81.14

新窗口打开| 下载CSV

图7

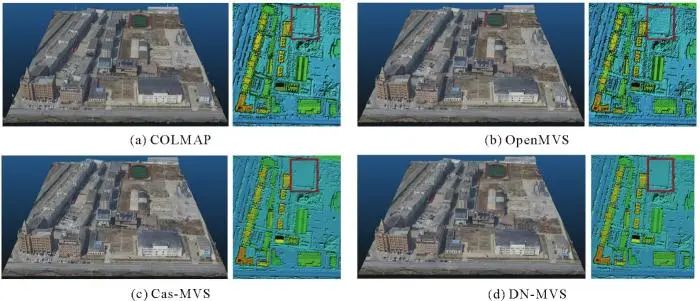
图7   在天津测试区的实景三维模型和DSM的可视化结果

Fig. 7   The visualization of 3D textured mesh and DSM results in the Tianjin test area

2.5　讨论

2.5.1　消融试验分析

本节对DN-MVS网络中的核心模块进行消融分析。核心模块包括深度辅助的表面法线估计模块、几何感知代价体构建及深度-法线联合优化模块，定量评价结果见表5。其中，试验1是进行深度估计的基准网络；试验2是在基准网络上引入法线估计模块；试验3是在试验2的基础上进一步引入几何感知代价构建策略；试验4在试验3基础上引入联合优化模块（即本文方法）。首先，与从推理深度图中计算得到法线的方式相比（试验1），表面法线估计模块的引入（试验2）显著提升了法线结果的精度。注意到该模块的引入造成了深度精度在PAG-D0.3 m指标上产生了轻微的下降，但在MAE和PAG-D0.6 m这两个指标上对深度图质量的提升起到了正向促进作用。这是由于在当前的消融结构中，法线估计模块与深度估计模块之间互相独立，增量模块的引入加大了网络的收敛难度，使得深度估计的性能出现震荡。这也反映了对二者进行后续的联合优化是非常必要的。接着，在上述基础上构建了具有几何感知的代价体（试验3）后，深度推理结果的精度获得了明显的提升，同时也辅助改善了法线推理结果的质量。最后，当引入深度-法线联合优化模块时（试验4），深度和法线结果的精度均得到了进一步的提升。这表明深度和法线的联合估计与优化能够显著增强深度学习多视密集匹配网络的整体性能。图8显示了上述消融试验的可视化效果表现，可以看出，随着各个关键模块的加入，深度和法线推理结果均逐渐精细化，地物边界结构更加清晰。

表5   对DN-MVS方法中核心模块的消融试验分析

Tab. 5  The ablative studies on the key modules of the DN-MVS method

消融设置	深度推理			法线推理
	MAE/m↓	PAG-D0.3 m/（%）↑	PAG-D0.6 m/（%）↑	mean/（°）↓	PAG-N20°/（%）↑	PAG-N30°/（%）↑
试验1	0.157	92.00	96.87	11.86	85.69	93.03
试验2	0.152	91.55	97.16	10.14	87.63	95.73
试验3	0.142	92.60	97.63	9.39	88.58	96.32
试验4（本文方法）	0.132	93.09	97.81	8.23	91.86	97.19

新窗口打开| 下载CSV

图8

图8   DN-MVS方法中核心模块消融试验的可视化结果

Fig. 8   The visualization results of ablative studies on the key modules of the DN-MVS method

2.5.2　损失函数分析

表6展示了在所构建的损失函数中，不同损失项对最终推理结果的影响。当移除深度-法线约束项和几何一致项、仅使用深度损失和法线损失这两个基本损失项时，深度精度和法线精度均产生了较为明显的下降，其中对法线质量的影响最为显著。当仅移除或 时，深度和法线精度也呈现出不同程度的降低，其中深度-法线约束项对精度的影响更加明显。根据试验情况，本文将深度损失项和法线损失项中的各权重参数经验性地设置为{3，2，3}。这是为了增强初始推理的深度和法线结果对反向传播的影响，并适当降低联合优化结果所占的比重，以确保初始深度推理和法线推理模块能够得到良好的训练，防止联合优化模块出现过拟合。表6对比了当权重参数{α1，α2，β}被设置为{1，1，1}时，深度和法线的推理精度。整体而言，本文方法对所采用的各损失项的敏感度较高，这说明使用多测度损失项是必要的；对使用不同权重参数的敏感度较低，但相比较而言，本文最终使用的权重{3，2，3}获得了更优的匹配质量。此外，本文沿用基准方法[13]的参数设置，将金字塔3阶段的权重参数分别设为{0.5，1，2}。表6额外测试了3阶段权重参数取值为{1，1，1}时对网络性能的影响，可以看出，增加高分辨率阶段推理结果的占比，更有助于获得更好的匹配结果。综合表6可知，各阶段的损失函数都有其必要性。

表6   损失函数中各组成项和各阶段权重参数的影响

Tab. 6  The effect of the components and the weighting parameters of each stage in the loss function

损失项设置	深度推理			法线推理
	MAE/m↓	PAG-D0.3 m/（%）↑	PAG-D0.6 m/（%）↑	mean/（°）↓	PAG-N20°/（%）↑	PAG-N30°/（%）↑
移除和	0.143	91.92	97.34	8.67	90.91	96.78
移除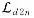	0.140	92.83	97.66	8.42	90.36	96.99
移除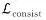	0.134	92.97	97.79	8.26	91.17	96.89
α1∶α2∶β=1∶1∶1	0.135	92.73	97.74	8.38	91.40	97.02
λ1∶λ2∶λ3=1∶1∶1	0.135	92.95	97.69	8.43	91.44	96.95
本文方法	0.132	93.09	97.81	8.23	91.86	97.19

新窗口打开| 下载CSV

2.5.3　模型复杂度分析

表7统计了本文提出的DN-MVS网络与其基准方法Cas-MVSNet，在推理过程中所需要的运行时间和显存占用情况。测试数据为WHU-OMVS瓦片测试集，影像大小为768×384像素，参与匹配的视角数量为5。由于本文方法是在基准方法上进行的增量式改进，新增的法线推理和联合优化模块导致了推理时间和显存占用稍有增加。尽管如此，DN-MVS计算复杂度的增长幅度在可接受范围内，仍可满足高效率的密集匹配和三维重建需求。

表7   DN-MVS与Cas-MVSNet的推理时间和显存占用比较

Tab. 7  Comparison of inference time and GPU memory between DN-MVS and Cas-MVSNet

方法	运行时间/s	显存占用/MB
Cas-MVSNet（基准方法）	0.15	2603
DN-MVS（本文方法）	0.23	2839

新窗口打开| 下载CSV

3　总结

本文介绍了一种改进的深度学习多视密集匹配方法，用于深度和表面法线的联合估计，以重建具有良好几何结构特征的三维场景模型。该方法充分利用深度和表面法线之间的相互几何约束关系，并将这种关系嵌入到基于深度学习的密集匹配网络中。通过在代价体中集成表面法线信息，构建了对几何敏感的代价体，以提升深度估计性能；利用初始深度估计值作为约束构建了局部代价体，实现精细的法线估计；利用可学习的联合优化模块进一步提高深度和法线图的质量。定量和定性试验证明了本文方法的有效性：与现有的典型多视密集匹配方法相比，本文方法在深度和表面法线估计任务上都具有更出色的性能，所重建的三维地表模型具有精细的细节和一致的平面几何结构。本文希望该项工作能够促进精细化三维场景重建方法的进一步发展和优化。

此外，所推理的表面法线是三维场景的重要视觉特征之一，对于理解三维场景的结构、纹理以及光照特性具有关键作用。因此，未来将考虑结合语义信息和表面法线，以识别和理解三维场景中的不同物体和结构，从而实现带有语义信息的多视密集匹配与三维场景重建。

初审：张艳玲

复审：宋启凡

终审：金   君