一文彻底搞懂机器学习 - 主成分分析（PCA）

主成分分析（Principal Component Analysis，简称PCA）是一种常用的线性降维技术，它通过提取数据中的主要成分来降低数据的维度，同时尽量保留数据的重要信息。

PCA的目的是将数据中最重要的特征提取出来，去掉冗余的信息，从而减少数据的维度，并且使得数据的解释更加直观。

PCA

一、线性降维

线性降维（Linear Dimensionality Reduction）是什么？线性降维是一种数据预处理技术，旨在通过线性变换将高维数据映射到低维空间，同时尽量保留数据的内在结构和信息。

这种技术通常用于减少数据的维度，以便更容易地进行可视化、存储、计算和分析。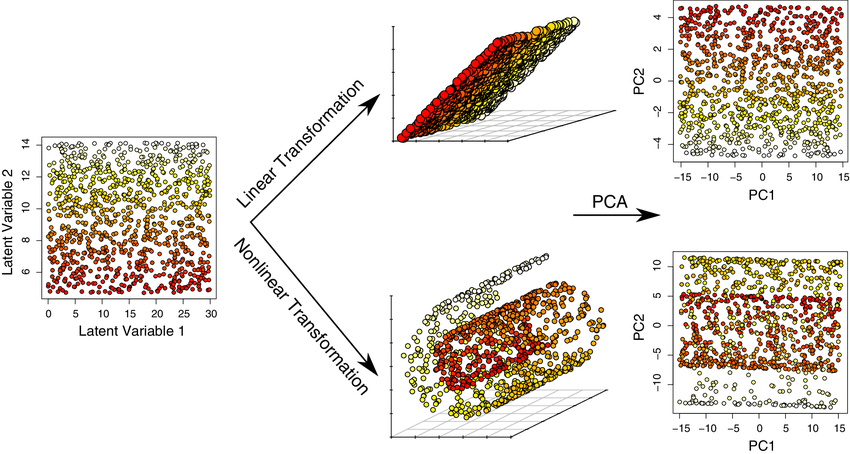

线性降维的实现原理是什么？在线性降维中，原始数据的高维特征通过线性组合被转换为低维特征 。这些低维特征通常是原始数据的一种“压缩”或“投影”，它们以更简洁的形式表示了数据的主要信息。

线性降维方法假设数据的主要结构是线性的，即数据点可以通过直线或平面等线性结构来近似。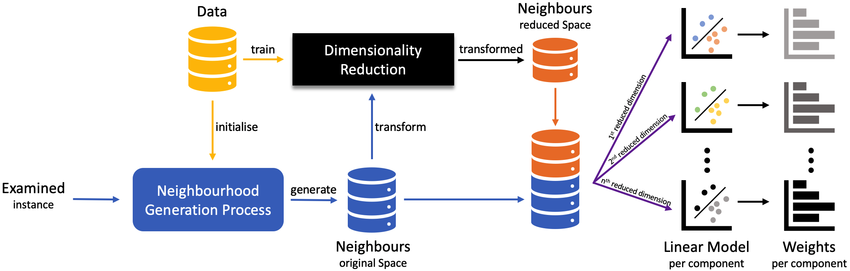

线性降维的算法有哪些？主成分分析（PCA）、线性判别分析（LDA）以及独立成分分析（ICA）。这些算法都试图通过线性变换将高维数据映射到低维空间，同时尽量保留数据的内在结构和信息。

主成分分析（PCA）：PCA是最常用的线性降维方法之一。它通过找到数据的主成分（即数据方差最大的方向）来将数据投影到低维空间。PCA的目标是最大化投影后的数据方差，从而保留数据的主要信息。
线性判别分析（LDA）：LDA是一种有监督的线性降维方法，它试图找到能够最大化类间方差同时最小化类内方差的投影方向。LDA通常用于分类任务中的特征提取。
独立成分分析（ICA）：ICA是一种寻找数据中独立成分的线性降维方法。它假设数据中的成分是非高斯的且相互独立的，通过最大化成分的独立性来提取数据的主要特征。

二、主成分分析

主成分分析（PCA）是什么？主成分分析是一种常用的数据降维技术，用于将高维数据转换为低维数据，同时尽量保留原始数据的主要信息。

在PCA中，原始数据通常被表示为一个矩阵，其中每一行代表一个数据点，每一列代表一个特征。PCA的目标是将这个矩阵转换为一个新的矩阵，其中新的列（即主成分）是原始数据的线性组合，并且这些新列是互不相关的（即它们之间的协方差为0）。这样，我们就可以通过选择前几个主成分来近似表示原始数据，从而实现降维。

转换矩阵：PCA的首要目标是将原始数据矩阵转换为一个新的矩阵。
线性组合：在新矩阵中，每一列（即每一个主成分）都是原始数据的一种线性组合。这意味着每个主成分都是原始数据各维度按一定比例加权求和的结果。
互不相关：这些新的主成分列之间是互不相关的。在数学上，这表现为它们之间的协方差为0。互不相关性意味着每个主成分都包含了原始数据中未被其他主成分所涵盖的信息。
降维：通过选择前几个主成分，我们可以近似地表示原始数据。由于这些主成分互不相关且按照方差（即信息含量）从大到小排列，因此选择前几个主成分通常能够保留原始数据中的大部分重要信息，同时实现数据的降维。

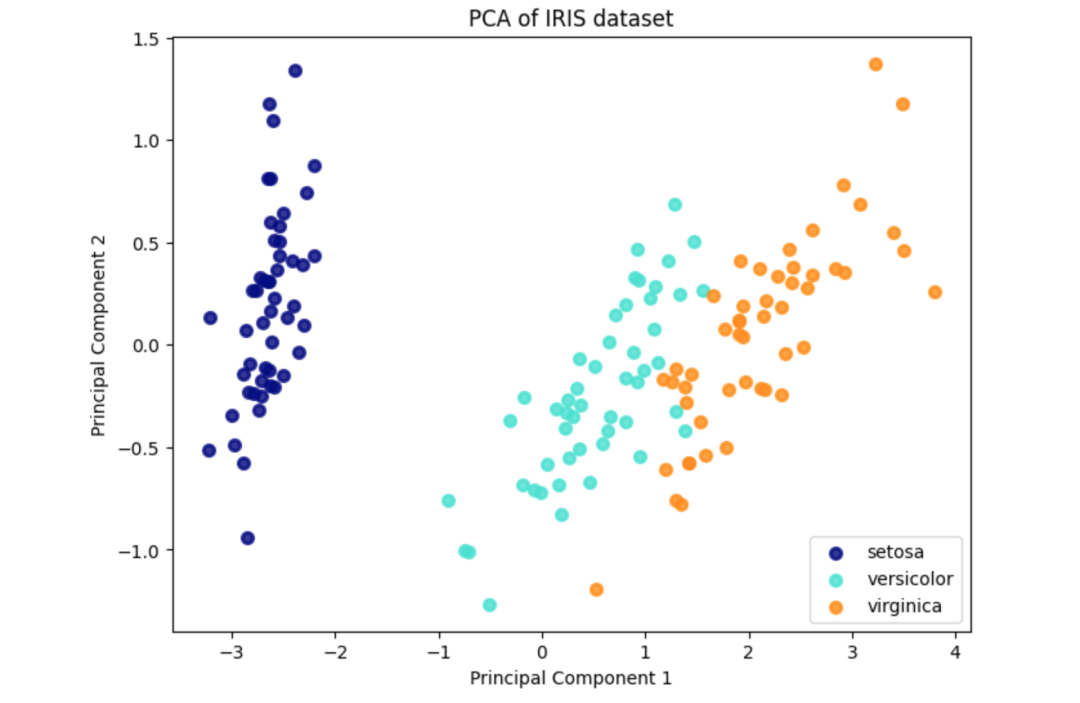
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.decomposition import PCAfrom sklearn.datasets import load_iris
# 加载数据集，这里使用Iris数据集作为示例data = load_iris()X = data.datay = data.target
# 初始化PCA模型，设置要保留的主成分数量pca = PCA(n_components=2)
# 对数据进行PCA降维X_pca = pca.fit_transform(X)
# 可视化降维后的数据plt.figure(figsize=(8, 6))colors = ['navy', 'turquoise', 'darkorange']lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], data.target_names):    plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=.8, lw=lw,                label=target_name)plt.legend(loc='best', shadow=False, scatterpoints=1)plt.title('PCA of IRIS dataset')plt.xlabel('Principal Component 1')plt.ylabel('Principal Component 2')plt.show()