一文彻底搞懂机器学习 - K均值（K-Means）

K均值（K-Means）是一种无监督的聚类算法，广泛应用于数据挖掘、图像分割、基因表达数据分析等领域。

K-Means算法旨在将n个数据点划分为k个聚类，使得每个数据点都属于与其最近的聚类中心所代表的聚类。每个聚类都有一个质心（即聚类中心），这些质心最小化了其内部数据点与质心之间的距离。

K-Means

一、无监督学习

无监督学习（Unsupervised Learning）是什么？无监督学习是从未标记的数据中发现隐藏的模式、结构和关系的机器学习技术。

与监督学习不同，无监督学习不需要事先定义数据的标签或类别，而是让算法自身去发现数据中的内在结构和规律。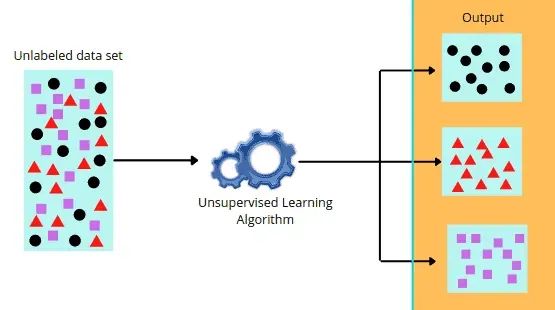

无监督学习的实现方法有哪些？聚类分析和降维技术是无监督学习的两大核心方法，其中K-means、DBSCAN和高斯混合模型是常用的聚类算法，而主成分分析、t-SNE和自编码器则是有效的降维技术。

聚类分析：

K-means：最常用的聚类算法之一，基于中心点将数据划分为K个簇，使得簇内样本间的平方和最小。
DBSCAN：基于密度的聚类算法，能够识别任意形状的簇，并处理噪声数据。
高斯混合模型（GMM）：假设数据服从多个高斯分布混合而成的概率分布模型，使用期望最大化（EM）算法估计参数。

降维技术：

主成分分析（PCA）：最常用的降维方法之一，通过线性变换将数据投影到较低维度的空间，同时保留数据的主要特征。
t-SNE：一种非线性降维技术，能够有效地保留原始高维数据的局部邻域结构，常用于可视化高维数据。
自编码器（AutoEncoder）：一种基于人工神经网络的无监督表示学习模型，通过编码器和解码器将输入数据映射到低维表示，并尝试重构原始输入。

二、K均值

K均值（K-Means）是什么？K均值（K-Means）是一种常用的聚类算法，属于无监督学习中的一种方法。

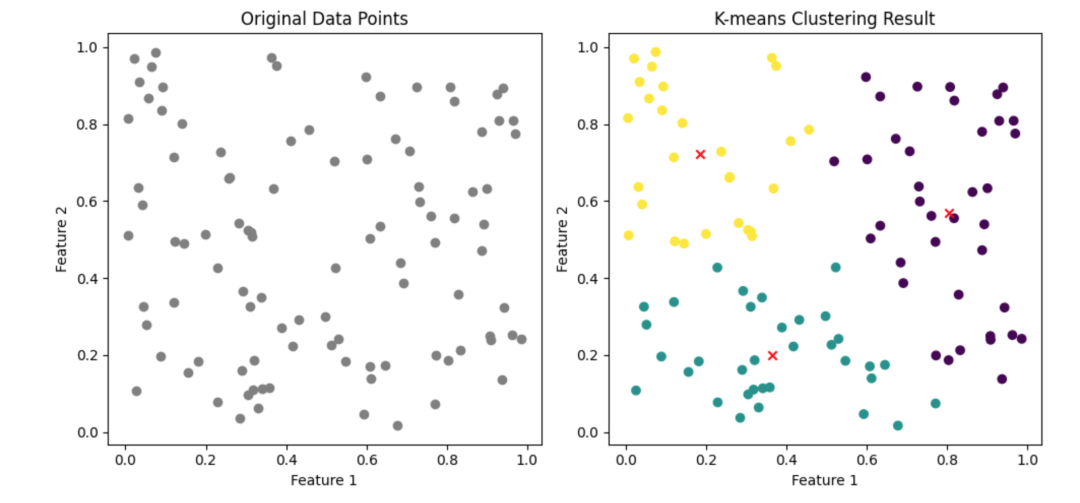
使用scikit-learn中的KMeans类对随机生成二维数据点进行聚类，并可视化展示原始数据点以及聚类后的结果，包括不同簇的数据点和聚类中心。

import numpy as npfrom sklearn.cluster import KMeansimport matplotlib.pyplot as plt
# 生成一些示例数据np.random.seed(42)  # 设置随机种子以获得可重复的结果X = np.random.rand(100, 2)  # 生成100个二维数据点
# 可视化原始数据点plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)  # 创建一个1行2列的子图，并选择第1个位置plt.scatter(X[:, 0], X[:, 1], c='gray', marker='o')  # 绘制原始数据点，使用灰色表示plt.title('Original Data Points')plt.xlabel('Feature 1')plt.ylabel('Feature 2')
# 使用KMeans进行聚类kmeans = KMeans(n_clusters=3, random_state=42)  # 假设我们要将数据分成3个簇kmeans.fit(X)
# 获取聚类结果labels = kmeans.labels_  # 每个数据点的簇标签centers = kmeans.cluster_centers_  # 聚类中心
# 可视化聚类结果plt.subplot(1, 2, 2)  # 选择第2个位置plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', marker='o')  # 绘制聚类后的数据点，使用不同颜色表示不同簇plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x')  # 用红色叉号标记聚类中心plt.title('K-means Clustering Result')plt.xlabel('Feature 1')plt.ylabel('Feature 2')
plt.tight_layout()  # 调整子图之间的间距plt.show()

K均值算法如何实现？K均值通过将数据集划分为K个不同的簇（组），使得每个数据点属于与其最近的均值点（即簇中心）所代表的簇。不断迭代更新聚类中心，将数据点分配到最近的簇中，直到聚类中心稳定，实现数据聚类。

初始化：随机选取K个样本点作为初始聚类中心。
计算距离：计算每个数据点与各个聚类中心的距离，通常使用欧氏距离的平方作为距离度量。
分配数据点：将每个数据点分配到离它最近的聚类中心所对应的簇中。
更新聚类中心：使用簇内数据点的均值作为新的聚类中心。
迭代：重复步骤2至4，直到聚类中心不再发生变化或达到预设的迭代次数。

使用Python实现自定义的KMeans聚类算法类，包括初始化聚类中心、迭代更新聚类中心和簇标签的逻辑，并通过示例数据展示了算法的聚类效果和可视化方法。

import numpy as np
class KMeans:    def __init__(self, n_clusters, max_iter=300, tol=1e-4):        self.n_clusters = n_clusters  # 聚类簇的数量        self.max_iter = max_iter      # 最大迭代次数        self.tol = tol               # 收敛容差        self.cluster_centers_ = None  # 聚类中心        self.labels_ = None          # 每个数据点的簇标签
    def fit(self, X):        # 随机初始化聚类中心        np.random.seed(42)  # 为了结果的可重复性        random_indices = np.random.permutation(X.shape[0])        self.cluster_centers_ = X[random_indices[:self.n_clusters]]
        for i in range(self.max_iter):            # 计算每个数据点到聚类中心的距离，并分配数据点到最近的簇            distances = self._compute_distances(X)            self.labels_ = np.argmin(distances, axis=1)
            # 计算新的聚类中心（簇内数据点的均值）            new_centers = np.array([X[self.labels_ == j].mean(axis=0) for j in range(self.n_clusters)])
            # 检查聚类中心是否收敛（变化是否小于容差）            if np.all(np.linalg.norm(new_centers - self.cluster_centers_, axis=1) < self.tol):                break
            self.cluster_centers_ = new_centers
    def _compute_distances(self, X):        # 计算X中每个点到聚类中心的欧氏距离        n_samples = X.shape[0]        distances = np.zeros((n_samples, self.n_clusters))        for k in range(self.n_clusters):            distances[:, k] = np.linalg.norm(X - self.cluster_centers_[k], axis=1)        return distances
    def predict(self, X):        # 对新数据点X进行聚类预测        distances = self._compute_distances(X)        return np.argmin(distances, axis=1)
# 使用示例


    
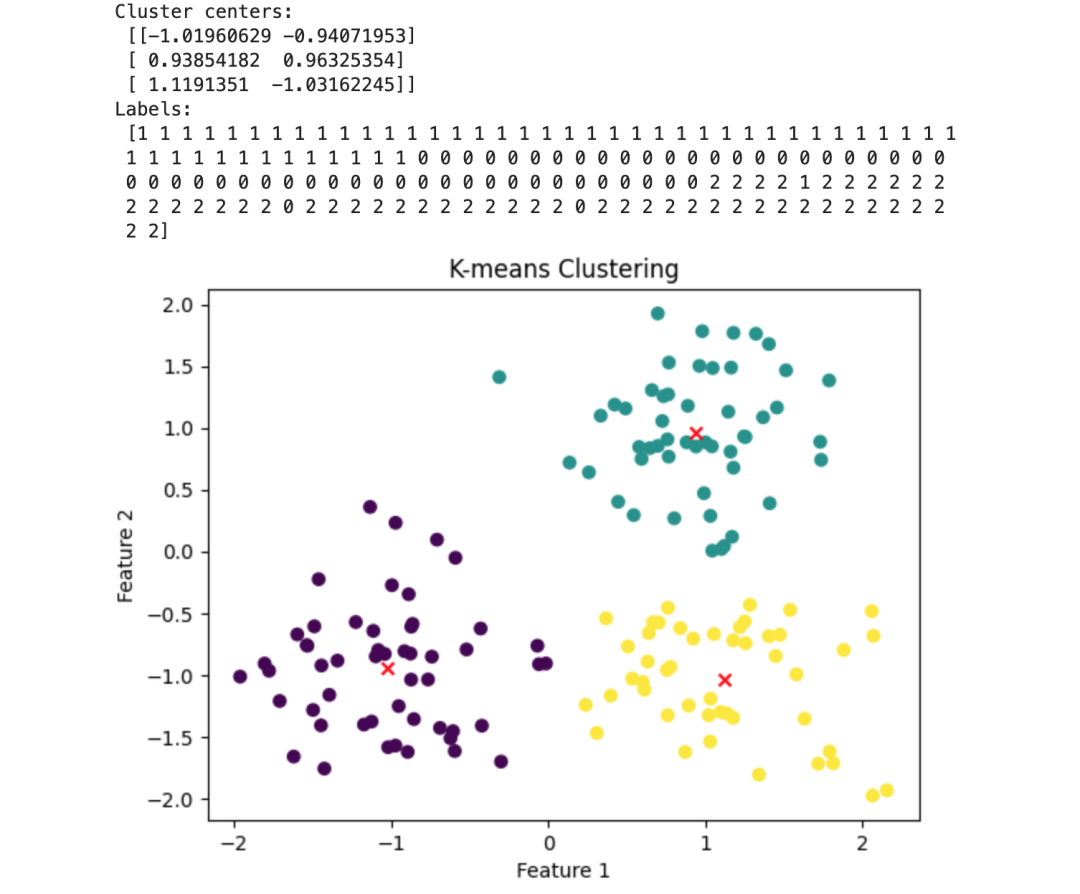
if __name__ == "__main__":    # 生成一些示例数据    np.random.seed(42)    X = np.vstack([np.random.normal(loc, 0.5, size=(50, 2)) for loc in [(1, 1), (-1, -1), (1, -1)]])
    # 使用自定义的KMeans类进行聚类    kmeans = KMeans(n_clusters=3)    kmeans.fit(X)
    # 打印聚类中心和每个数据点的簇标签    print("Cluster centers:\n", kmeans.cluster_centers_)    print("Labels:\n", kmeans.labels_)
    # 可视化聚类结果（需要matplotlib库）    import matplotlib.pyplot as plt    plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis', marker='o')    plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x')    plt.title('K-means Clustering')    plt.xlabel('Feature 1')    plt.ylabel('Feature 2')    plt.show()