Nat Commun发表!浙大湖州研究院×浙大数学学院联合推出受控加速优化算法PIDAO，实现深度学习模型训练难点破解!

在人工智能领域，深度学习技术凭借其强大的深度函数逼近能力，不仅可以为机器人运动规划、聚变等离子体预测与控制等复杂的受控智能系统提供超越传统方法的服务，还不断推动着技术边界的拓展，在众多工程和科学任务中展现出卓越性能，赢得广泛认可与青睐。

然而，在深度学习的广泛应用背后，也面临着不小的挑战。其核心问题之一在于解决大规模优化问题，即训练拥有数百万甚至数十亿个决策变量的深度神经网络（NNs）。这一过程不仅复杂耗时，而且深度学习模型的训练损失图景往往高度退化，存在多个局部和全局最小值，并进一步导致模型的泛化能力和性能存在显著差异。

为了应对这一挑战，研究者们通常采用基于梯度的优化算法如来寻找高维变量空间中的合适最小值。尽管这些方法在一定程度上加速了训练过程，但理解优化对深度学习模型的泛化和逼近影响仍然是一个难题。此外，现有优化器在面对复杂损失图景时，也可能陷入局部最小值或收敛缓慢的问题。

▍跨学科研究，提出创新解决方案PIDAO

针对这一问题，来自浙江大学控制学院许超教授、蔡声泽研究员团队联合数学学院刘康生教授团队前不久对此进行了深入研究，并将闭环反馈控制与优化算法建立联系，创新性地提出了一种面向深度学习的受控加速优化算法PIDAO（注：PIDAO读作“辟道”）。

研究团队通过引入虚拟物理学进行了优化过程建模。具体而言，他们采纳了经典力学的二阶常微分方程（ODE）作为建模基础，将复杂的优化问题转化为在高维参数空间中的导航控制任务。算法通过精确计算误差的比例、积分和微分项，生成反馈控制信号，驱动优化器在损失图景中高效探索并定位最优解。

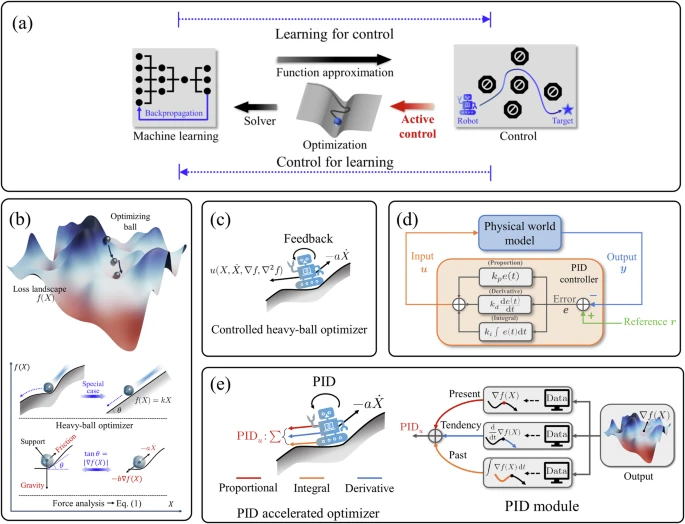
闭环主动控制优化器在解决优化问题中的概述

研究团队不仅提升了优化算法的收敛速度和精度，还显著增强了其鲁棒性和可解释性，实现了对优化流程的主动调控。通过李雅普诺夫稳定性分析，他们证明了PIDAO在无约束凸和非凸设置下的全局和局部收敛结果，并推导出适用于深度学习问题的离散化迭代公式。实验结果表明，PIDAO在降低泛化误差和加速训练收敛方面表现出色，且计算成本更低。与当前多种先进方法相比，PIDAO在多个基准测试案例中均取得了更优表现。

该研究不仅为深度学习模型的快速训练提供了新途径，其提出的虚拟物理学与控制理论等学科交叉方法也为深度学习研究开辟了新方向。通过整合数值优化、动力系统理论、控制理论及数值计算等多个领域的知识，该研究团队为深入理解深度学习的训练机制贡献了新颖的研究视角。

相关论文发表信息

目前，该研究工作的相关论文已在国际顶级期刊《自然·通讯（Nature Communications）》上进行了发表。论文标题为“Accelerated optimization in deep learning with a proportional-integral-derivative controller”，作者团队包括陈嵩、刘佳旭、王鹏凯、许超、蔡声泽、褚健。其中通讯作者由浙江大学控制科学与工程学院副院长、浙江大学湖州研究院院长许超教授和浙江大学控制科学与工程学院蔡声泽研究员共同担任。

那么，该研究工作具体内容为何呢？接下来和机器人大讲堂一起深入了解~

▍融合“现在、过去与未来”，打造加速神经网络训练新利器

当前，针对高维优化问题，业界普遍采用基于梯度的算法，如动量优化器、梯度下降（GD）以及Adam等。这些方法通过迭代更新参数来逼近最优解，但在实际应用中仍存在诸多不足。例如，动量优化器虽然能够加速收敛，但其对参数选择的敏感性以及易陷入局部最优的问题限制了其性能；GD和Adam算法虽然在一定程度上缓解了这些问题，但在面对复杂损失函数时可能表现出不稳定性和收敛速度慢的特点。此外，这些算法往往缺乏严谨的理论框架和可解释性，这使得研究者在优化过程中难以准确把握算法的行为和性能。   

针对以上问题，研究团队将控制科学中广泛使用的比例－积分－微分（PID）反馈控制律应用于深度学习的优化过程，从而开发出连续时间PID加速优化器（Proportional-Integral-Derivative Accelerated Optimization, PIDAO）。这一方法的提出，为加速神经网络的训练提供了新的视角和工具。

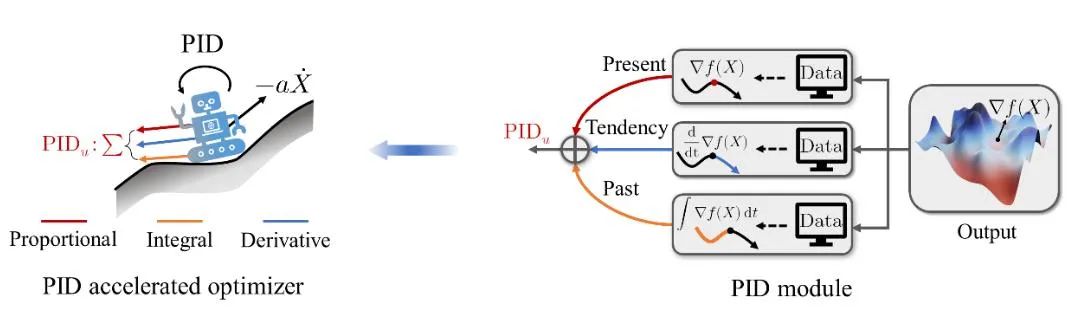
用于深度学习的PID加速优化算法的基本思想

PID控制律通过比例（P）、积分（I）和微分（D）三个环节来调节系统的输出，以达到预期的控制目标。PIDAO的核心思想便在于，将优化过程视为一个虚拟的物理动力学系统，通过PID控制律来调控这一系统的行为，以实现对优化过程更为精细和全面的调控。在PIDAO中，这三个环节分别对应于（当前“地势”）、历史梯度积分（过往“地势”）以及前方梯度趋势（未来“地势”）三类信息。

具体来说，PIDAO不再单一地依赖梯度来调控优化方向，而是通过PID反馈机制，综合考虑当前梯度、历史梯度积分以及前方梯度趋势，来控制寻优机器人的导航过程。这种融合三类信息共同决策寻优的方式，使得PIDAO在面对复杂损失函数时能够表现出更高的稳定性和更快的收敛速度。

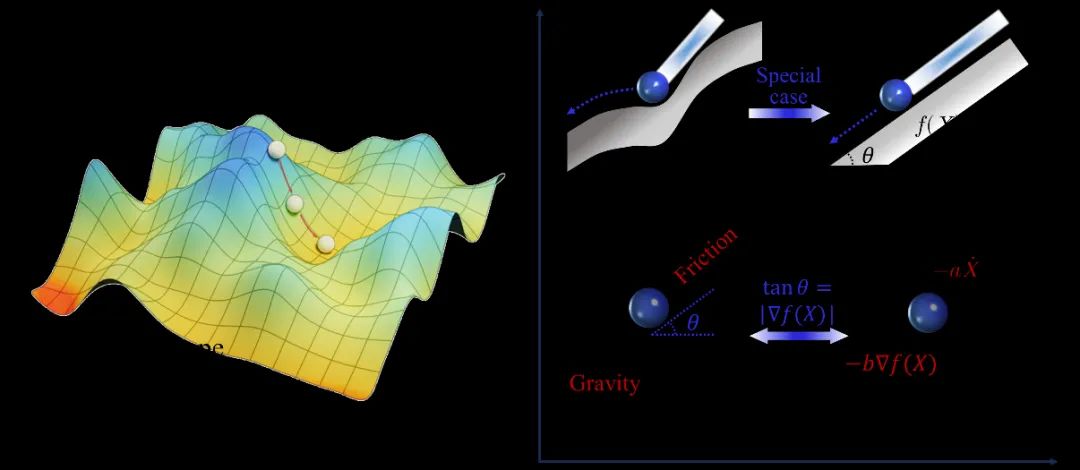
重球法（Heavy-ball optimizer）的动力系统观点，利用Lyapunov稳定性分析算法收敛性

此外，PIDAO还通过构建合适的Lyapunov函数来建立超参数与稳定性之间的关系，以及动力系统平衡点与高维参数空间训练问题最优性的关联。这一理论框架的提出，不仅增强了PIDAO的可解释性，还为优化过程中的参数选择提供了理论依据。

▍赋予PIDAO优化器参数可解释性，提升深度学习准确性和效率

在深度学习领域，算法的准确性和效率一直是研究人员追求的目标。通过深入探索PIDAO的特性，研究团队也揭示了其在提高深度学习准确性和效率方面的显著优势。

研究团队基于Lyapunov稳定性理论，为PIDAO在凸优化问题和非凸优化问题中提供明确的超参数选取范围，增强了PIDAO在实际应用中的可操作性，这为其在复杂优化问题中的表现奠定了坚实基础。更关键的是，研究团队发现了PIDAO优化器的抵消效应。此效应赋能PIDAO在导航错综复杂的损失函数地形时，能够更有效地调和梯度下降过程中的波动性与收敛速率，进而实现对最优解的精准锁定，使得PIDAO在处理高维度、非线性特征的深度学习挑战时，表现出更为出众的稳健性和探索能力。

PIDAO 针对低维（非）凸优化的性能

除了抵消效应外，PIDAO优化器的另一大亮点是其超参数的可解释性。借助PID控制器与PIDAO优化器之间的联系，研究人员可以根据具体的优化任务，更直观地调整PIDAO的超参数，以达到最佳的优化效果。这一发现不仅降低了优化算法的使用门槛，也促进了PIDAO在更多深度学习场景中的应用。

为了将PIDAO优化器应用于实际的神经网络训练，研究团队采用了多种离散化方法对PIDAO离散化，并成功地将PIDAO集成到了如Pytorch等深度学习框架中。这一举措极大地拓展了PIDAO的实用性，使得研究人员和开发者能够轻松地将其应用于自己的深度学习项目中。通过与深度学习框架的紧密集成，PIDAO优化器得以在更广泛的场景中发挥其优势，可为深度学习的准确性和效率提升提供有力支持。

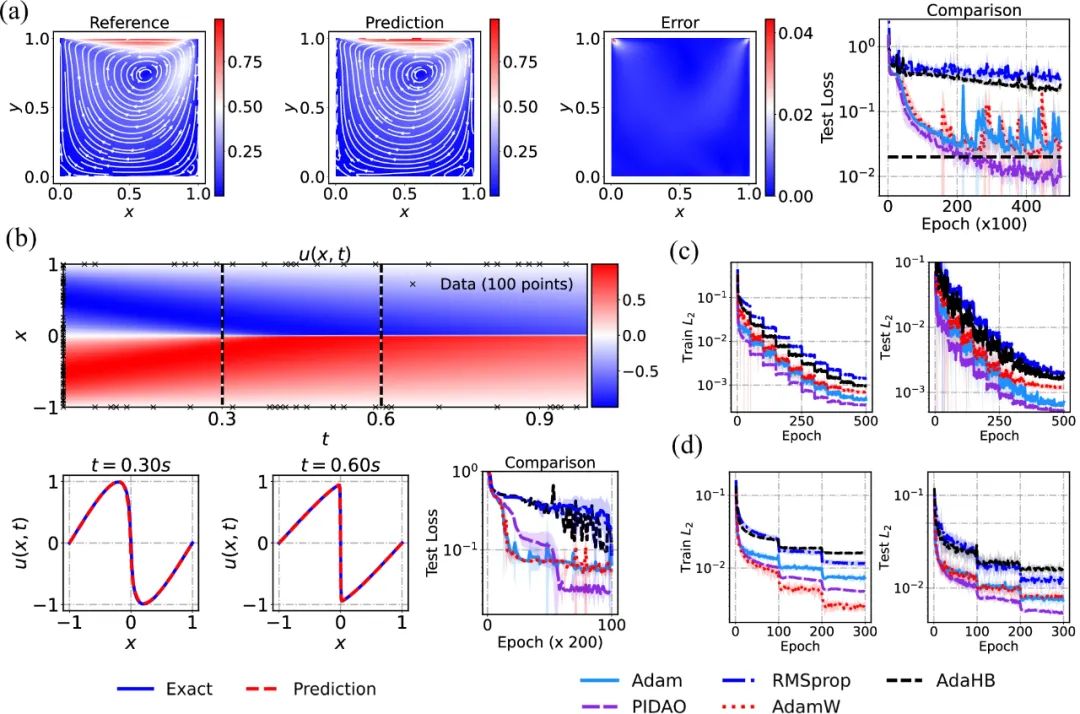
PIDAO与Adam等经典算法在神经网络求解偏微分方程问题上的性能对比

在多个测试场景中，研究团队还将PIDAO系列算法与基准优化算法（如Adam）进行了全面对比。结果显示，PIDAO系列算法不仅取得了更高的训练精度，还实现了更快的收敛速度。这一优异表现充分验证了PIDAO优化器的有效性和潜力。与传统优化算法相比，PIDAO在深度学习任务中展现出了更加出色的性能，为研究人员提供了更加高效、准确的优化工具。

▍结语

PIDAO优化器的提出，不仅有助于加速深度学习模型的训练，提高模型的性能和效率，更为基于控制理论方法研究深度学习问题提供了全新的思路。这一创新性的成果，有望推动深度学习领域的进一步发展，为人工智能技术的进步注入新的活力。

随着研究团队对PIDAO优化器的持续探索和创新，我们有理由相信，PIDAO将在深度学习领域发挥越来越重要的作用，成为推动人工智能技术进步的关键力量。

参考文章

https://doi.org/10.1038/s41467-024-54451-3

 

 

看累了吗？戳一下“在看”支持我们吧