👇 连享会 · 推文导航 | www.lianxh.cn


🍓 课程推荐:连享会:2025 寒假班
嘉宾:连玉君(初级|高级);杨海生(前沿)
时间:2025 年 1 月 13-24 日
咨询:王老师 18903405450(微信)

温馨提示: 文中链接在微信中无法生效。请点击底部「阅读原文」。或直接长按/扫描如下二维码,直达原文:

作者:浦进博 (中山大学)
邮箱:pujb@mail2.sysu.edu.cn
1. 简介
合成控制法与回归控制法,作为面板数据中备受推崇的因果推断手段,尤其擅长于处理组中个体数量稀少的场景。当前,这两种方法的统计验证主要依赖于安慰剂检验,然而,该检验所需的前提假设 (诸如随机分组) 往往难以在现实中达成。鉴于此,Chen 等 (2024) 引入了分位数回归技术,通过估算处理个体反事实结果的 2.5% 与 97.5% 分位数,巧妙地构建了每期处理效应的 95% 置信区间。然而,传统的线性分位数回归不仅收敛缓慢,还可能因函数设定不当而引入偏差。
为了克服这一难题,Chen 等 (2024) 提出了“分位数随机森林”这一机器学习方法,用于执行分位数回归,并据此构建了处理效应的置信区间。他们将此方法命名为“分位数控制法” (QCM)。作为一种非参数的集成学习范式 (例如,随机森林由 1000 棵决策树的平均结果构成),QCM 在面临异方差、自相关或函数误设等复杂情况时,仍能展现出强大的稳健性。
本文将介绍该方法的原理以及 Stata 实现。
2. 理论背景
在现有文献中,关于 SCM (合成控制法) 框架下治疗效果估计和推断的一个关键操作假设是, 和 之间存在横截面关系。我们假设 和 之间的关系由下式表征:
其中, 是一个未知的条件密度函数。上式意味着如果治疗从未发生,则治疗单元在所有控制单元条件下的结果分布将随时间保持稳定。
传统 SCM 假设治疗单元和控制单元的结果之间存在线性关系 (Abadie 等,2010;Hsiao 等,2012;Amjad 等,2018;Cattaneo等,2021),即:
其中 是 (伪) 真实线性投影参数, 是误差项。为了预测
的 (条件) 均值,需要估计 。虽然这种线性设定使得SCM易于实施和解释,但它遗漏了一些重要信息。
- 一方面,某些潜在因素可能对不同个体产生不对称影响,导致设定错误。
- 另一方面,即使在很多情况下,我们可以将线性合成控制视为真实过程的合理近似,但在关注均值预测时,不可避免地会忽略关于分位数的分布信息。例如,当一个地区的邻近地区经济衰退时,该地区更可能经历负面冲击,这表明该地区经济增长的分布向左偏移,并且在观察到邻近地区负增长率时,可能具有较厚的左尾部。
如果我们只关注条件均值,则可能会存在上述两种问题;而使用分位数随机森林的方法将会很好避免设定错误的问题,同时能够将分布信息描述更加准确全面。
2.1 数据
记 ,。
2.2 算法
对于处理后期间 的处理效应的 预测区间。
- Step1:使用处理前数据,通过随机森林 (QRF) 在分位数 和 上运行 对 的分位数回归。
- Step2:对于每个处理后期间 ,使用步骤 1 的结果和对照单元的处理后数据 计算条件分位数 和 。
通俗总结这套算法就是:利用随机森林技术来构建 100 棵决策树。这些树在构建过程中,会随机选择数据样本和特征指标。当这些树完成训练后,它们会各自给出一个预测结果。然后,在这 100 个预测结果,找出其中 2.5% 和 97.5% 分位点的预测值,这样就形成了一个预测区间。这个区间可以被用来估计反事实结果的可能性范围。
3. Stata 实操
3.1 安装命令
ssc install qcm, all replace
3.2 命令介绍
qcm depvar [indepvars] , trunit(#) trperiod(#) [options]
以下是一些重要的选项:
模型设置
counit(numlist):用于作为捐赠池的控制单元;preperiod(numlist):干预发生前的预处理时期;-
postperiod(numlist):干预发生及之后的后处理时期。
最优化设置
mtry(int):在每棵树上随机抽取作为候选的预测变量数量;minlsize(int):每个终端节点所需的最小观测值数量;minssize(int):分裂节点所需的最小观测值数量;fill(fil_method):用于填充缺失值的方法;cilevel(#_c):设置置信水平;默认为 95% 的置信区间。
安慰剂检验
placebo([{unit|unit(numlist)} period(numlist) cutoff(#_c)]):使用虚假处理单元进行空间安慰剂检验,或使用虚假处理时间进行时间安慰剂检验。
3.3 应用1:2004 香港经济一体化
下面的代码提供了一个实际应用的例子:
. use growth, clear
. xtset region time
. * 列出所有的标签,显示时间标签为2004年第一季度的单元编号。
. label list
. di tq(2004q1)
. /* 对GDP变量实施量化控制方法,其中trunit(9)指定处理单元为第9个单元 (这里指香港)
> trperiod(176)指定处理时间为第176个时间点。*/
. qcm gdp, trunit(9) trperiod(176)
. * 使用第三种风格的置信区间
. qcm gdp, trunit(9) trperiod(176) cistyle(3)
. * 实施空间安慰剂测试,其中预处理的均方预测误差 (MSPE) 是处理单元的两倍或更大的个体被删除。
. qcm gdp, trunit(9) trperiod(176) placebo(unit cut(2)) frame(growth)
. /* 显示时间标签为2002年第一季度的单元编号,这里是为了设置一个虚假的处理时间点,
> 实施时间安慰剂测试*/
. di tq(2002q1)
. qcm gdp, trunit(9) trperiod(176) placebo(period(168)) savegraph(growth, replace)
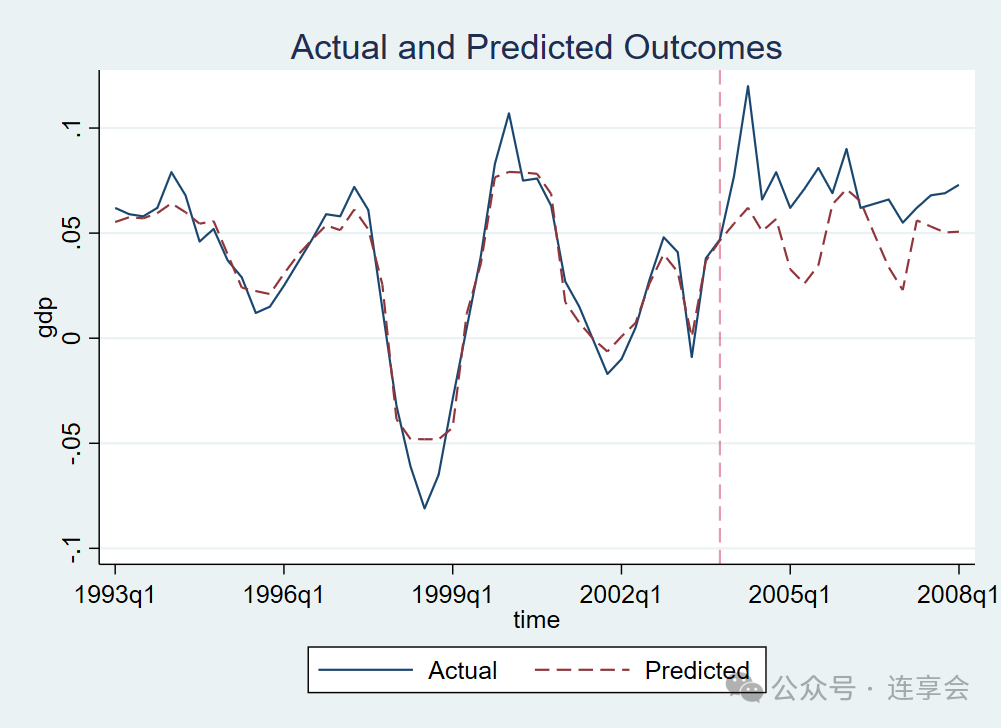
时间安慰剂检验中,2002-2004 年期间拟合效果较好,通过检验。
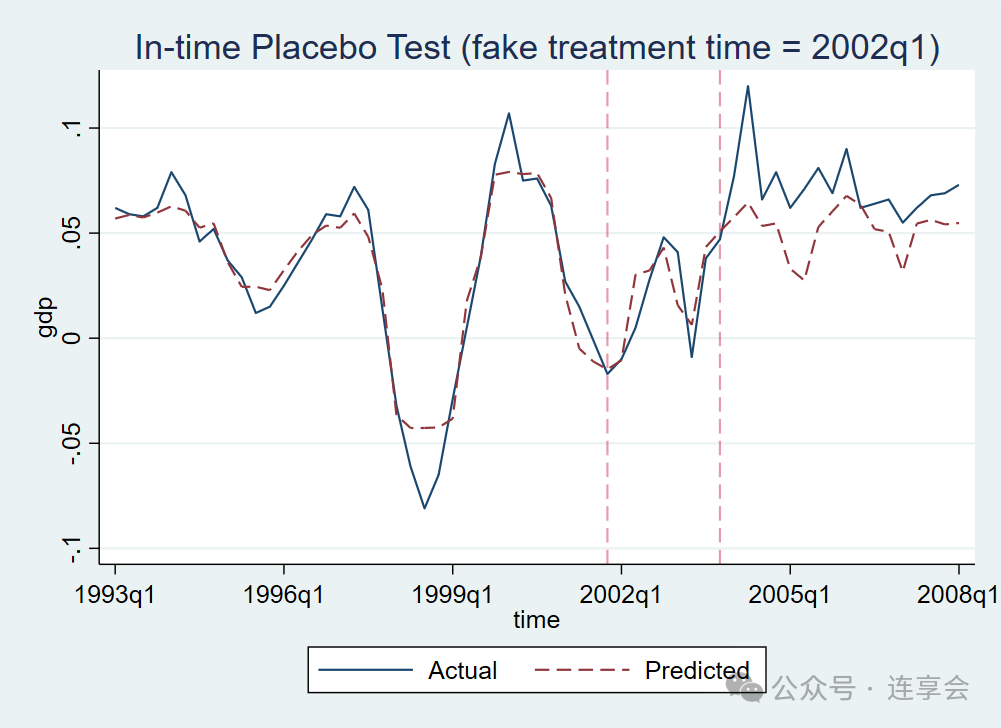
空间安慰剂检验中,可以算出经验 值为 0.5263,未通过检验。
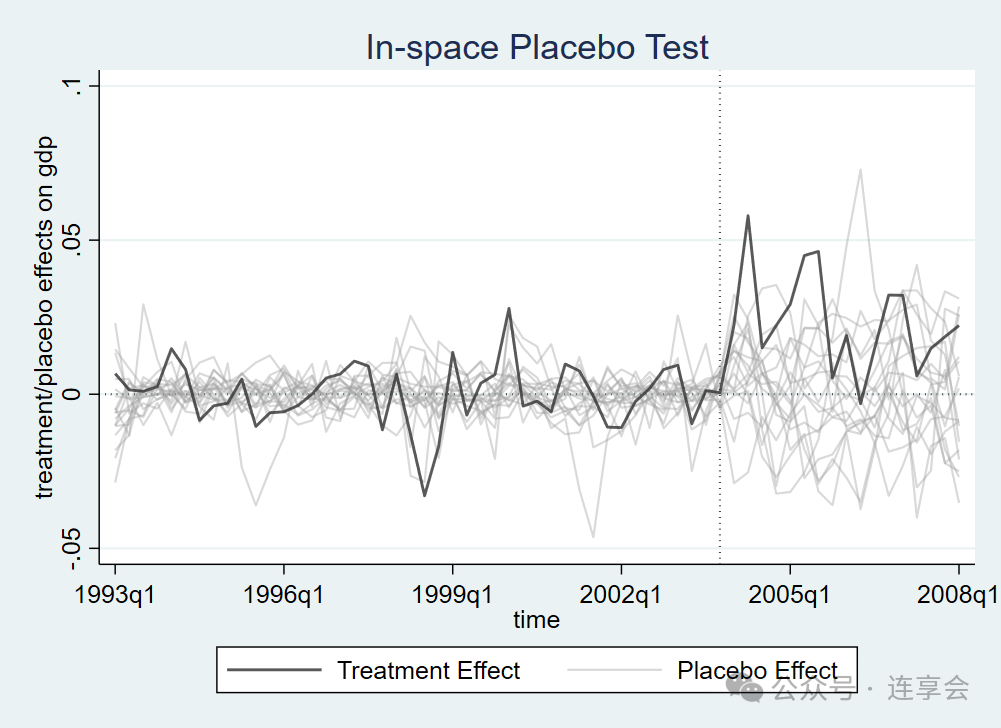
置信区间如下图所示,可以看到政策在实施后第二个季度存在正向显著的影响,之后的政策效果不显著异于零。
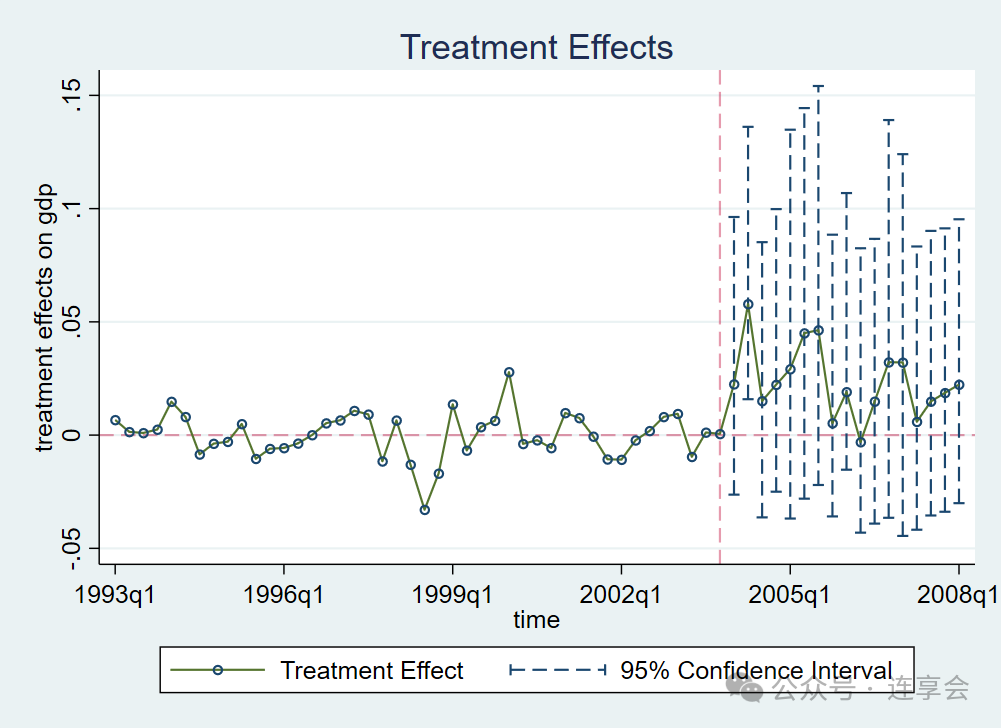
3.4 应用2:1989 禁烟法案
. lxhuse smoking,clear
. xtset state year
. qcm cigsale, trunit(3) trperiod(1989)
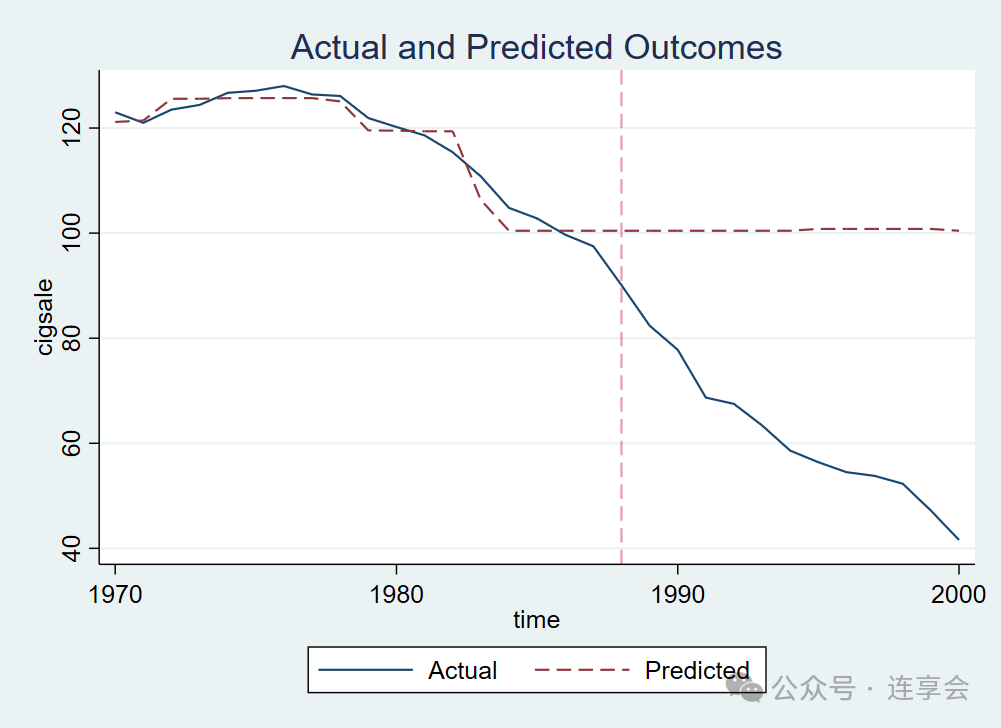
在上方展示的图表中,我们惊讶地发现,QCM 的预测结果竟然呈现为一条水平线!
这一现象背后的原因在于,随机森林算法本质上是一种上高维空间的“分段常数函数”。当训练数据中的协变量取值范围限定在 100 至 120 之间时,若测试数据包含低于 100 的值,算法会将这些数据归入训练集中最接近的节点,即 100 所在的节点。由此,便产生了所谓的“尾部聚集”效应。
4. 总结
在本文中,我们探讨了合成控制法 (SCM) 的最新进展,特别是将机器学习技术与 SCM 结合的创新方法——分位数控制法 (QCM)。QCM 通过分位数随机森林方法,有效地解决了传统线性分位数回归在处理异方差、自相关或函数误设等问题时的局限性。这种方法不仅提高了预测的稳健性,还能够提供更全面的分布信息,从而为因果推断提供了新的视角。
5. 参考文献
- Chen, Q., Xiao, Z., & Yao, Q. (2024). Quantile control via random forest. Journal of Econometrics, 105789. -Link- -PDF- -Google-
6. 相关推文
Note:产生如下推文列表的 Stata 命令为:
lianxh 合成控制 随机森林, m
安装最新版 lianxh 命令:
ssc install lianxh, replace
- 伍站锋, 2022, Stata:纠偏合成控制法介绍-allsynth, 连享会 No.854.
- 何庆红, 2020, Synth_Runner命令:合成控制法高效实现, 连享会 No.205.
- 何庆红, 2020, 合成控制法 (Synthetic Control Method) 及 Stata实现, 连享会 No.119.
- 周瑾, 2024, sdid_event命令:合成DID事件研究法, 连享会 No.1482.
- 李晶晶, 2022, 合成控制法简介, 连享会 No.910.
- 李胜胜, 2021, Stata:随机森林算法简介与实现, 连享会 No.532.
- 浦进博, 2024, Stata:非参数合成控制法命令—npsynth, 连享会 No.1458.
- 郭盼亭, 2023, Stata:基于Lasso的合成控制法-scul, 连享会 No.1167.
- 陈勇吏, 2020, Stata:合成控制法-synth-命令无法加载-plugin-的解决办法, 连享会 No.204.
- 陈少廷, 2022, Stata:合成控制法介绍-synth2, 连享会 No.1133.
- 马丁, 刘梦真, 2021, 机器学习:随机森林算法的Stata实现, 连享会 No.568.
- 高净鹤, 2022, Stata:合成控制法的预测区间-scpi, 连享会 No.1096.

🍓 课程推荐:公开课:Stata+R 软件基础
嘉宾:候丹丹
扫码进群 获取资料及听课链接!

尊敬的老师 / 亲爱的同学们:
连享会致力于不断优化和丰富课程内容,以确保每位学员都能获得最有价值的学习体验。为了更精准地满足您的学习需求,我们诚挚地邀请您参与到我们的课程规划中来。请您在下面的问卷中,分享您 感兴趣的学习主题或您希望深入了解的知识领域 。您的每一条建议都是我们宝贵的资源,将直接影响到我们课程的改进和创新。我们期待您的反馈,因为您的参与和支持是我们不断前进的动力。感谢您抽出宝贵时间,与我们共同塑造更加精彩的学习旅程!https://www.wjx.cn/vm/YgPfdsJ.aspx# 再次感谢大家宝贵的意见!


New! Stata 搜索神器:lianxh 和 songbl GIF 动图介绍
搜: 推文、数据分享、期刊论文、重现代码 ……
👉 安装:
. ssc install lianxh
. ssc install songbl
👉 使用:
. lianxh DID 倍分法
. songbl all

🍏 关于我们
- 直通车: 👉【百度一下: 连享会】即可直达连享会主页。亦可进一步添加 「知乎」,「b 站」,「面板数据」,「公开课」 等关键词细化搜索。
