机器学习（朴素贝叶斯）

来源：算法日常小记

朴素贝叶斯算法作为机器学习中经典算法，在机器学习分类任务中占据一席之地，尤其是在文本分类，垃圾邮件分类等问题上具有不错的泛化能力，作为最简单的生成式模型，下面我们具体了解下。

概率基础知识

条件概率：设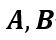

是两个事件，且

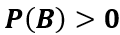，则在事件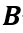

发生的条件下，事件

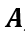发生的概率为：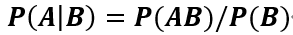

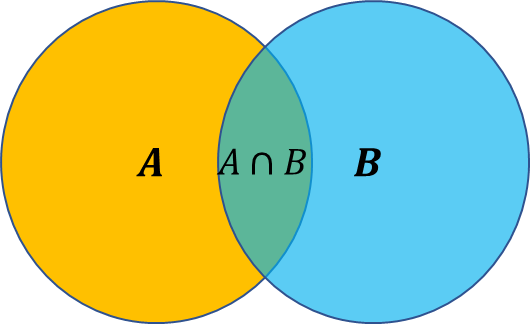
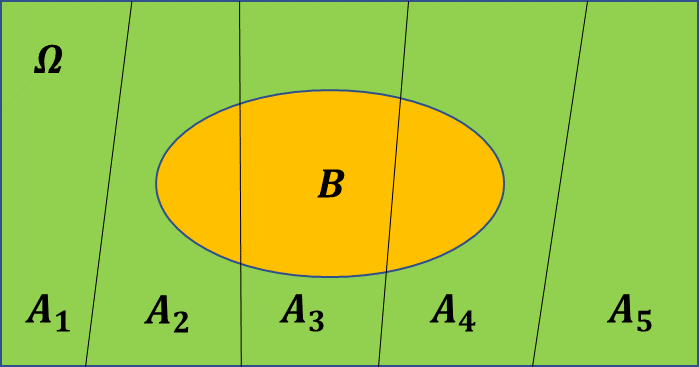
条件概率由文氏图可以更好的理解，其中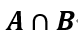

就是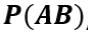

乘法公式：由条件概率公式得

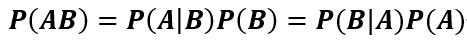
乘法公式推广：对于任何正整数，当时有：

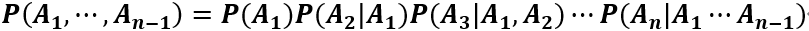
全概率公式：若事件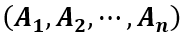两两互斥，即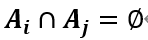，并且

，则对任意一个事件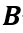，有如下公式成立

全概率由文氏图可以理解为

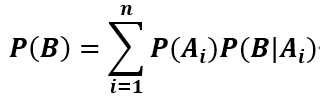
贝叶斯公式：由上面几个公式不难推出下面公式

朴素贝叶斯分类算法

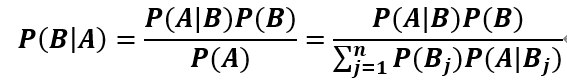
现在我们将上述贝叶斯公式应用到机器学习算法中，分类任务是已知特征预测类别的有监督学习任务，上述贝叶斯公式可写为：

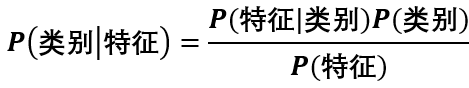
假设现在有个二分类问题，根据男士条件来预测女士嫁与不嫁，具体数据如下表：

身高	长相	收入	嫁与否
高	帅	高	嫁
矮	丑	低	不嫁
高	丑	低	不嫁
高	丑	高	嫁
矮	帅	低	不嫁
矮	丑	高	不嫁
矮	帅	高	嫁
高	丑	高	嫁

已有历史数据，现来了一个男士新的特征（矮，帅，高），来进行预测嫁与不嫁，根据贝叶斯公式我们可以得到以下两个公式，比较两个值的大小就可以预测出嫁与不嫁，不难看出我们只需要比较分子的大小就可以。

朴素贝叶斯算法假设各个特征之间相互独立，所以

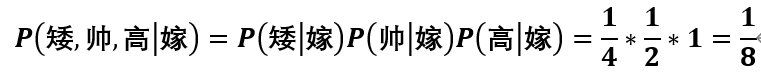
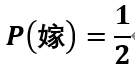
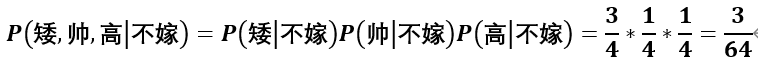
可见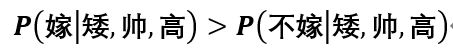，所以预测结果为嫁。

拉普拉斯平滑

现在又来了一个男士新的特征（矮，帅，低），来进行预测嫁与不嫁，当我们进行计算

时，发现为0，这就会导致

的最后概率为0，而这个错误的造成是由于训练量不足，会令分类器泛化能力大大降低，为了解决这个问题加入拉普拉斯平滑，它的思想非常简单，就是对每个类别下所有划分的计数加1，公式为：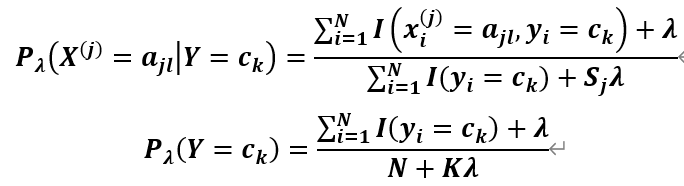

其中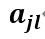

代表第j个特征的l个选择，

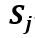代表第j个特征的个数，

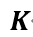代表种类，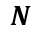

代表样本数，

。

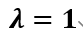加入拉普拉斯平滑后，我们看下特征（矮，帅，低）在嫁与不嫁的概率结果，

首先看

，首先身高的特征类别为2种，

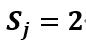，所以分母为6（嫁的个数4+特征类别数2），分子为2（嫁中为矮1+

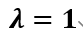），概率为1/3，按同样的方式求得

，

，最后结果为：

接下来就要用第二个公式求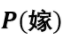，其中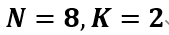，则最后概率为1/2。所以分子部分的概率为1/72。接下来用同样的方法求的分子部分概率为：

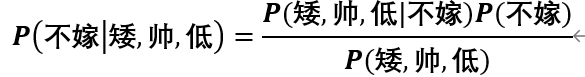
其中分子部分为：

后者概率大于前者，所以预测为不嫁。

频率派VS贝叶斯派

在参数估计上，频率派是MLE(最大似然估计)，贝叶斯派是MAP(最大后验估计)

具体不同，可查看
https://www.zhihu.com/question/20587681

朴素贝叶斯分类算法的优缺点

优点：算法逻辑简单，易于实现，分类过程中时间空间开销比较小

缺点：理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

声明：部分内容来源于网络，仅供读者学术交流之目的。文章版权归原作者所有。如有不妥，请联系删除。