| 《Deep-learning models for forecasting financial risk premia and their interpretations》https://www.researchgate.net/publication/370747157_Deep-learning_models_for_forecasting_financial_risk_premia_and_their_interpretations |
文章主要解决预测金融市场风险溢价的问题。作者将预测任务分解为时间序列和横截面模型，并利用跳跃连接的神经网络来提高模型性能。此外，通过引入可解释的方法——LIME，增强了模型的透明度，使其在金融风险管理和投资决策中具有实际应用价值。 |
• • • 引言• • •
金融风险溢价的测量是资产定价中的一个重要问题。风险溢价是指风险资产相对于无风险资产的预期超额回报，其估计对于投资者和资产定价模型都至关重要。
作者指出，由于资产回报的噪声性和非平稳性，使用机器学习（ML）技术来估计风险溢价面临挑战。在回顾Fama和MacBeth（1973）以及Fama和French（1993, 2015）的经典研究后，作者认为尽管线性模型在风险管理中广泛使用，但金融市场的复杂性意味着线性关系往往不足以捕捉资产因子与超额回报（风险溢价）之间的全部相互作用。
• 本文目标：利用机器学习方法，特别是深度学习，来预测风险溢价，并解决现有ML模型的“黑箱”问题，即模型的不透明性。
• 本文方法：将风险溢价预测分解为两个独立任务：时间序列模型和横截面模型，并使用具有跳跃连接的神经网络来训练深度神经网络。
本文核心的问题是解决风险溢价的估计，核心的方法可以分解为两个步骤。第一步是对于风险的分解，第二步是神经网络的设计。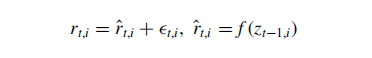
其中可以将个股在某时刻的超额收益分解为预测超额收益加上预测误差。𝑟𝑡,𝑖是观测到的超额回报，𝑟^𝑡,𝑖 是预测的超额回报，𝜖𝑡,𝑖是预测误差，𝑓是待学习的模型，𝑧𝑡−1,𝑖是输入特征。同时本文引入了均方误差（MSE）作为损失函数，用于评估模型预测的准确性。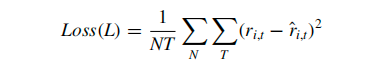
具体而言，作者将风险溢价预测分解为两个独立的任务：时间序列模型和横截面模型。时间序列模型预测平均月回报，横截面模型预测回报的横截面偏差。
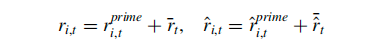
作者提出将月度回报 𝑟𝑖,𝑡分解为两部分：平均回报 𝑟ˉ𝑡和偏离平均的回报𝑟𝑖,𝑡(prime)。注意此处的平均回报是指全市场的平均回报，因此该变量即为时序部分预测，而个股偏离市场平均回报的部分即为横截面预测。
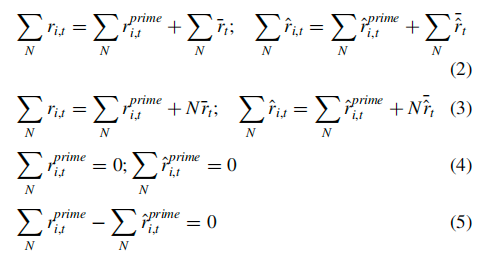
以上公式推导中比较关键的是从公式（3）到公式（4）的步骤，主要依据是下面公式中市场平均收益的定义，公式右侧全市场股票在月度平均收益的定义即为左侧股票总收益除以N个时间段。将上面公式代入公式（3）中即能推导出整体超额收益为0。
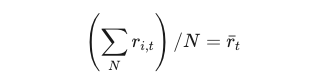
因此可以根据上面的公式对损失函数做进一步推导：
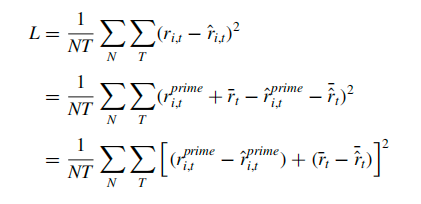
可以看到在最后公式的左边即为界面损失，右边为时序损失。作者提出，当训练单一模型 f 时，最小化上面公式中两个部分的损失可能并不合适。由于这些损失是独立的，作者认为应当分别针对每个部分进行优化，因此需要有两个独立的模型。于是后文的模型一是预测月平均回报的时间序列模型，模型二是捕捉横截面变化的截面网络，通过预测与平均值的偏差来实现。还有一个原因是，我们都知道股票市场回报是非平稳的。而使用机器学习的一个重要假设是样本外数据分布与样本内数据分布应当相同，然而由于股票市场数据的非平稳性，这一假设被违反了。因此从股票收益中移除时间序列成分会使剩余的横截面成分均值为零。理论上这会使得横截面模型的训练更容易。1. 问题背景
• 通常情况下，增加神经网络的层数会增加网络的容量，但当层数增加到一定程度后，网络性能会开始下降。这种现象不仅限于过拟合，即使在添加了正则化层（如批量归一化层）后，性能退化问题依然存在。
• 现有的深度学习优化器难以训练非常深的网络，可能是由于梯度消失或爆炸问题。
2. 跳跃连接（skip connections）
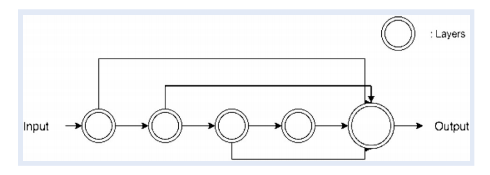
• 受到ResNet（He et al. 2016）和DenseNet（Huang et al. 2017）的启发，作者设计了一种新的模型架构，在每一层和最后一层之间添加跳跃连接。
• 跳跃连接允许每一层的输出直接传递到最后一层，从而避免了梯度消失或爆炸的问题，使得可以训练更深的网络。
• 具体来说，作者提出的模型在每一层和最后一层之间添加了跳跃连接。这种修改允许训练多达10层的神经网络而不出现性能退化，甚至可以达到更好的性能。实际上，这种架构的性能在15层时达到饱和，可能是由于最后一隐藏层的大小爆炸。
数据集
本文使用的数据集主要来自CRSP（Center for Research in Security Prices）数据库，涵盖了1957年3月至2016年12月期间在纽约证券交易所（NYSE）、纳斯达克（NASDAQ）和AMEX（American Stock Exchange）上市的公司的月度股票回报数据。以下是对数据集的详细介绍：
• 股票回报数据：包含约6,200只股票每个月的回报数据。回报数据包括总回报和超额回报。
• 公司特定特征：共使用了94个公司特定的特征。这些特征包括61个每年更新一次的特征，13个每季度更新一次的特征，20个每月更新一次的特征。还包括74个变量，对应于其标准工业分类（SIC）代码的前两位。
• 特征排名和归一化：对股票特征进行横截面排名，并将排名归一化到区间[−1,1][−1,1]，以消除异常值的影响。
• 宏观经济数据：使用Treasury bill rate作为无风险利率的代理变量。• 数据被分割为训练集、验证集和测试集。训练集包含了1957年至1986年的数据，验证集为1987年至1998年的数据，测试集为1999年至2016年的数据。• 使用滚动窗口方法进行模型训练，即每年对模型进行重新训练，使用前12年的数据作为验证集，使用更早的数据作为训练集。
公司特征
|
| mom1m | 1个月的动量 |
mvel1 | 公司市值 |
| retvol | 回报的波动性 |
| turn | 股票换手率 |
| dolvol | 美元交易量 |
| mom12m | 12个月的动量 |
| std_turn | 流动性的波动性 |
| indmom | 行业动量 |
| mom6m | 6个月的动量 |
| zerotrade | 零交易天数 |
| ill | 流动性不足 |
| chmom | 6个月动量的变化 |
|
SP | 价格销售比 |
| baspread | 买卖价差 |
| maxret | 最大日回报 |
| idiovol | 特质波动性 |
| ntis | 净股本扩张 |
| ep | 收益价格比 |
宏观经济特征
|
| 短期利率 |
|
| 长期利率 |
|
| 通货膨胀率 |
|
| 工业生产指数 |
|
| 失业率 |
|
| 消费者信心指数 |
|
| GDP增长率 |
|
| 货币供应量 |
|
结果分析
下表展示了不同机器学习模型在横截面风险溢价预测中的表现。表格中的R(OOScs)2表示样本外的横截面𝑅2值，用于衡量模型的预测能力。表格中的模型分为两类：一类是基于总回报训练的模型，另一类是基于横截面回报训练的模型。
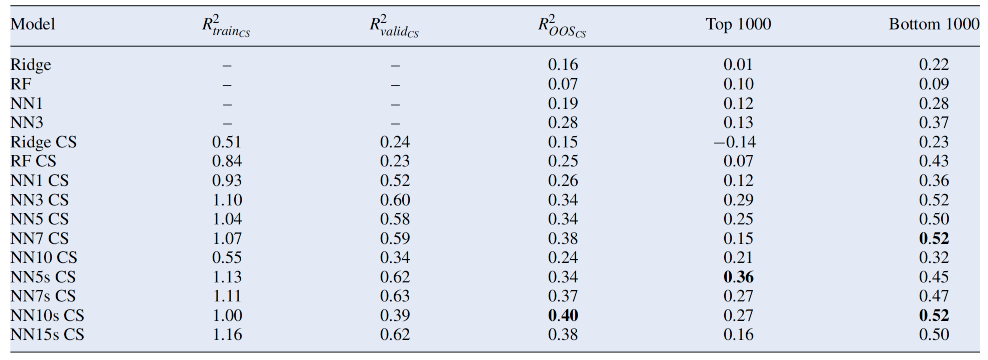
• 基于横截面回报训练的模型表现优于基于总回报训练的模型。• 神经网络模型的性能在7层时达到饱和，但在使用跳跃连接的情况下，可以训练到10层且性能没有下降。
• 深度神经网络模型（如NN10s CS）在训练集上的R2值最高，可能表明存在过拟合的风险。下表展示了不同模型在总回报预测中的表现。表格中的R(OOS)2表示样本外的总回报R2值，用于衡量模型的整体预测能力。
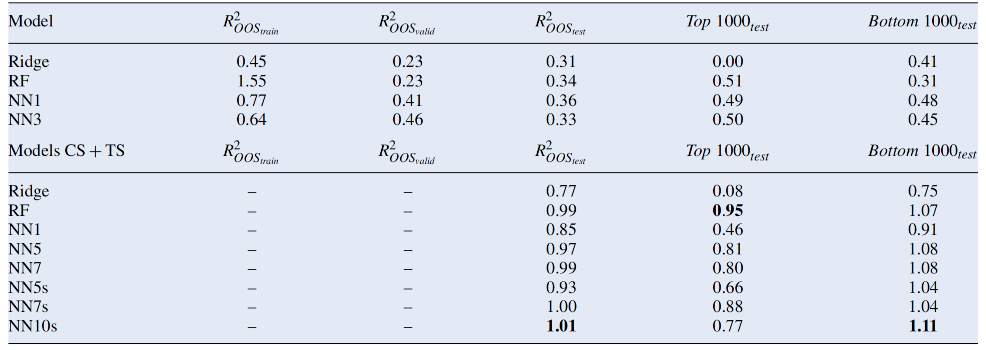
• 组合模型（CS+TS）的表现显著优于单一基于总回报训练的模型。• 使用跳跃连接的神经网络模型（如NN10s CS）在样本外测试中表现最佳，R(OOS)2提高了三倍。下面作者对表现最优的模型TS + NN10s CS进行性能分析。在上面的结果中可以看到横截面模型的性能显著优于基于总回报的模型。神经网络模型在7层时性能达到饱和，但使用跳跃连接的神经网络模型可以训练到10层，且性能没有下降。
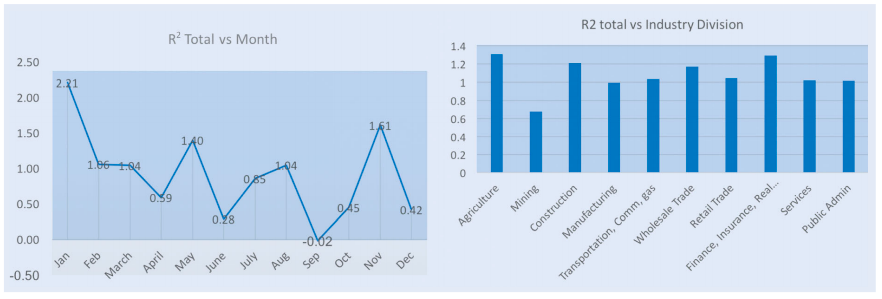
从年度和月度的角度去分析，最佳模型（TS+NN10s CS）的年度性能在某些年份表现不佳，可能是由于市场波动性增加（如2000年、2005年、2006年、2007年、2011年和2014年）。月度性能显示9月份表现最差，可能与“九月效应”有关。
• 作者在每个月的开始，根据模型对股票的预测回报进行排序，将股票分为十等分（即十分位数），采用简单的长-短策略，即购买预测回报最高的十分位的股票（长），卖空预测回报最低的十分位的股票（短）。
• 创建了两种类型的投资组合：等权重投资组合和按市值加权的投资组合。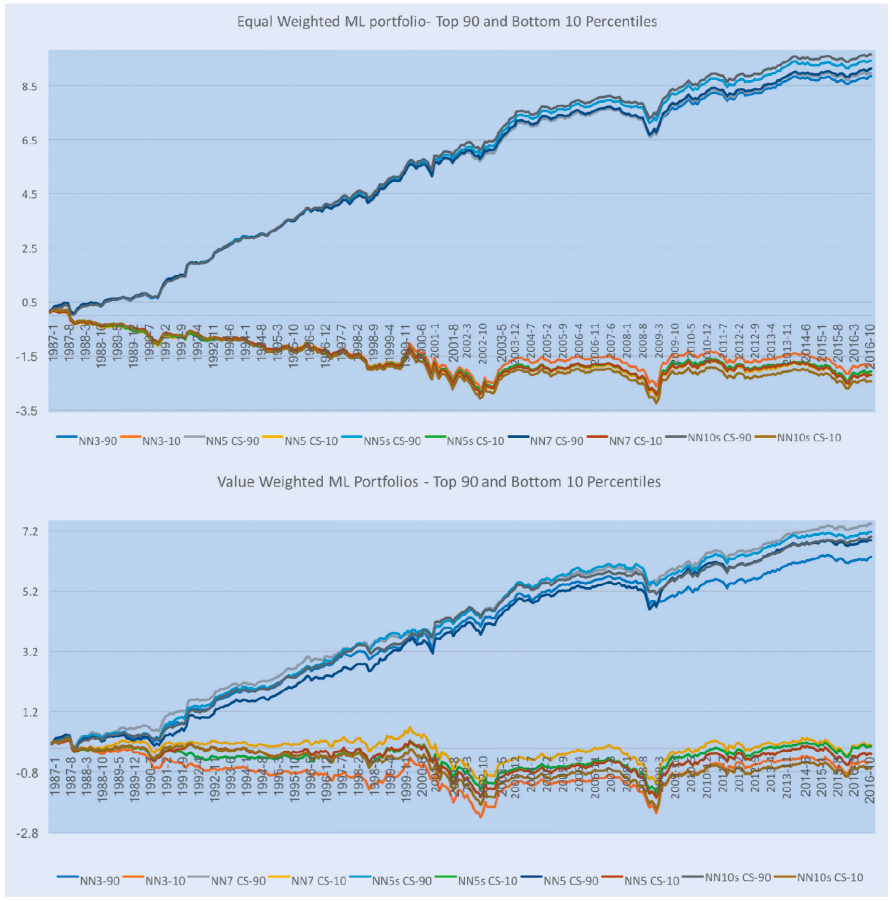
使用不同模型构建的投资组合显示，等权重投资组合的夏普比率较高，最大回撤较小。等权重投资组合的累积对数回报也高于价值加权投资组合。这一部分主要探讨了深度学习模型的可解释性，特别是如何通过局部近似方法解释黑盒模型的预测结果。本章使用了LIME（Local Interpretable Model-Agnostic Explanation）方法来解释深度神经网络的预测行为。LIME方法通过扰动输入数据点并计算每个扰动数据的预测值，来近似决策边界。然后，使用加权岭回归模型来确定每个特征在预测中的贡献。对于每个测试点，LIME可以计算出特征的重要性或贡献。
上图中展示了单个数据点的领先特征及其重要性。对于这个例子，短期反转（mom1m）是对模型预测贡献最大的特征，并且与预测的横截面回报负相关。
通过对所有数据点的特征重要性进行聚合，可以得到全局特征重要性。
上图为前15个最重要的特征的全局特征重要性。结果显示，短期反转（mom1m）、公司规模（mvel1）和回报波动性（retvol）是最重要的三个特征。
直方图展示了LIME系数（即特征重要性）的分布情况。对于重要特征，直方图有较长的尾部，例如mom1m、size和turnover。大多数特征的行为与现有文献一致，但也有一些特征的关系与文献不一致，例如流动性波动性（std_turn）。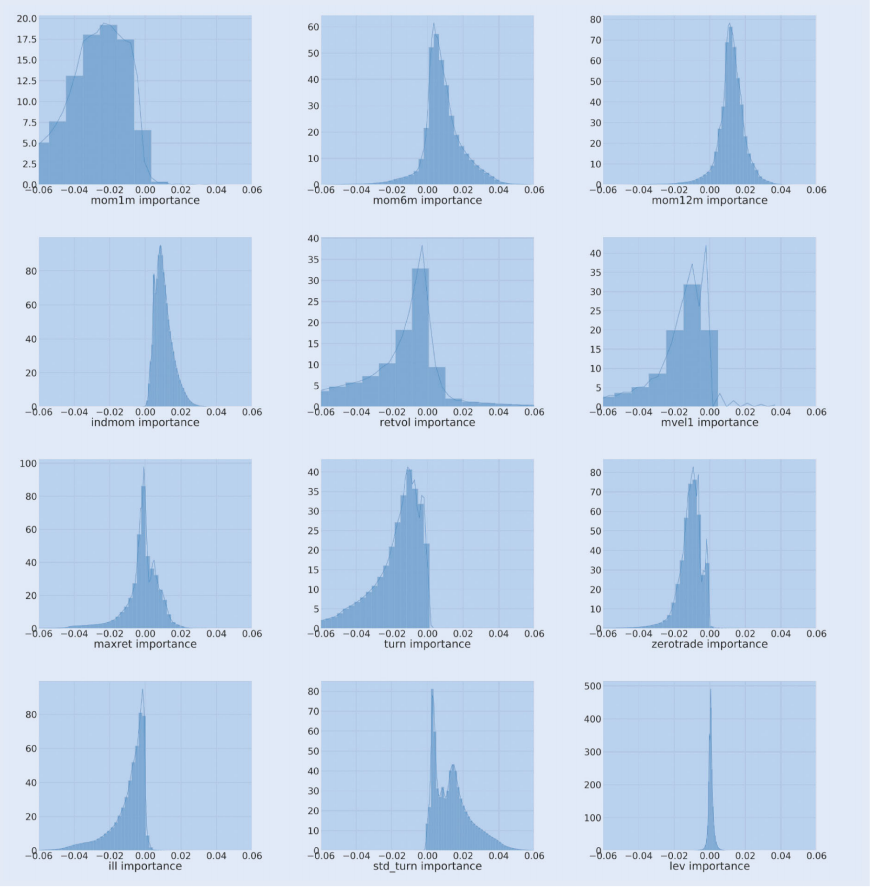
• 短期反转（mom1m）：与回报负相关，直方图显示大的负系数。• 12个月动量（mom12m）：与回报正相关，直方图显示大的正系数。• 行业动量（indmom）：如果某个行业表现良好，该行业内的公司表现也可能较好，直方图显示大的正系数。• 公司规模（mvel1）：小盘股表现优于大盘股，直方图显示正系数。• 回报波动性（retvol）：回报波动性与回报的关系不确定，直方图显示正负两方面的关系。• 换手率（turn）：高换手率的股票风险溢价较小，直方图显示负系数。• 流动性波动性（std_turn）：流动性波动性应与风险溢价负相关，但模型显示正相关，需进一步验证。本文展示了如何使用机器学习方法预测金融市场的风险溢价，并通过分解为时间序列和横截面模型来解决非平稳性问题。研究结果表明，深度神经网络模型在预测风险溢价方面优于线性模型，并且通过使用跳跃连接可以训练更深的模型。此外，论文还通过LIME方法对深度学习模型的解释性进行了分析，增加了投资者对模型预测的信心。总体而言，该方法为投资组合构建、绩效归因和风险管理提供了一个稳健的框架，并有助于更好地理解影响风险溢价的因素。• 模型深度问题：尽管通过跳连接解决了深度神经网络性能下降的问题，但模型在超过一定层数后仍可能出现性能饱和或下降的现象。• 数据集限制：LIME方法虽然提供了一种解释深度模型预测的方法，但其适用性仍限于某些类型的模型和数据集，特别是对于非图像相关的数据集和卷积神经网络模型。• 市场异常波动：模型在某些年份（如2000年、2005年、2006年、2007年、2011年和2014年）的预测表现较差，可能是由于市场的高波动性引起的，这需要进一步研究和改进。• • • End• • •
公众号开通合作功能，欢迎有需求的企业和个人点击公众号后台消息查看
Time is an ally.
