

这篇文章探讨了理解和构建机器学习(ML)模型所需的核心数学概念。我们将深入研究线性代数和微积分,展示它们在模型训练和优化中的应用。最终,你将对这些基础知识及其实际应用有更精确的理解。
数学在机器学习中的重要性
数学是机器学习的基石。理解算法背后的数学原理可以帮助你理解模型的工作原理、为何做出特定预测以及如何提升模型性能。对于机器学习来说,两个最关键的数学领域是线性代数和微积分。
线性代数处理大型数据集,涉及矩阵乘法和变换等操作,是构建和优化机器学习模型的基础。向量之间的距离可以帮助我们对数据进行归一化,或者将正则化项添加到损失函数中,或作为通过深度神经网络层的一部分变换。
另一方面,微积分在学习过程中至关重要,用于理解这些模型中的变化和优化。例如,计算梯度是训练算法(如梯度下降)所必需的。
掌握这些数学概念可以让你开发更高效的算法,排除问题,并提高解决复杂问题的能力。通过深入研究机器学习的数学原理,你可以不再将模型视为黑盒,开始理解驱动它们的复杂机制。
数学在机器学习中的重要性2
扎实的数学基础对于任何想要在机器学习领域取得卓越成绩的人来说都是必不可少的。数学不仅是理论上的;它是支撑每个机器学习算法的实用工具。以下是它的重要性:
模型理解与开发:数学让你从根本上理解模型的工作原理,使你能够开发或改进新模型。
算法优化:基于微积分的优化技术对于最小化误差和提高模型准确性至关重要。
数据处理:线性代数提供了有效处理和操控大型数据集的方法,这在数据预处理和模型训练中至关重要。
性能提升:正则化等数学概念有助于防止过拟合,从而增强模型对新数据的泛化能力。
问题解决:扎实的数学基础使你具备系统地解决复杂问题的分析能力。
线性代数和微积分在机器学习中的应用
数学在机器学习中有着深度的应用。以下是线性代数和微积分在各种机器学习算法中的应用概述:
线性代数在机器学习中的应用
向量和矩阵:机器学习算法经常使用向量和矩阵来表示数据。例如,整个数据集可以表示为一个矩阵,每一行描述为一个向量(即数据集中的一个样本)。如果 X 是数据矩阵,每行 x_i 代表一个数据点。
矩阵运算:矩阵乘法用于数据变换、距离计算和执行各种线性变换。例如,在神经网络中,输入数据 X 与权重矩阵 W 相乘,得到 Z = XW。
特征值和特征向量:这些用于降维技术,例如主成分分析(PCA),其中数据的协方差矩阵 C 被分解为其特征值和特征向量,以转换到一个新的坐标系,数据方差排列轴。
奇异值分解(SVD):SVD 用于推荐系统和解线性系统。为此,我们将矩阵 A 分解为三个矩阵:
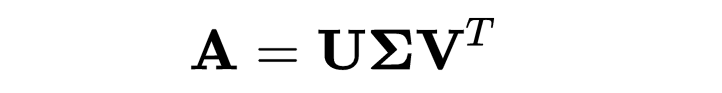
其中 U 和 V 是正交矩阵,Σ 是对角矩阵。
微积分在机器学习中的应用
导数和梯度:
导数度量函数的变化率(即任意点的斜率)。在机器学习中,梯度(偏导数的向量)用于最小化损失函数。例如,在梯度下降中,我们按如下方式更新参数 θ:
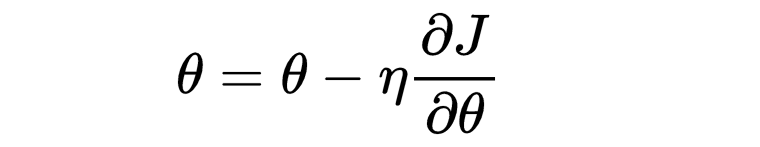
其中 J 是损失函数,η 是学习率。
链式法则:链式法则用于反向传播,以计算神经网络中每个权重的损失函数梯度。如果函数 f 由两个函数 g 和 h 组成,即 f(x) = g(h(x)),那么 f 的导数如下:
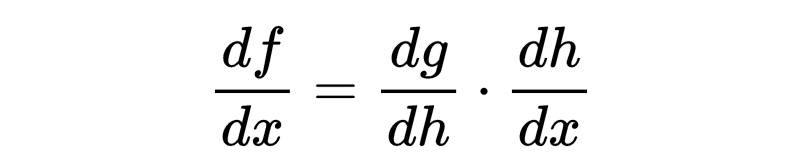
优化技术:基于微积分的技术(例如梯度下降)对于训练模型至关重要。这些技术包括计算梯度,以迭代地更新模型参数以减少损失。例如,梯度下降中参数 θ 的更新规则为
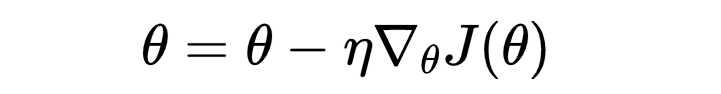
向量范数
一个函数

被称为范数,如果它满足以下性质:
非负性:对于所有 x^2∈Rx^2,有 f(x)≥0f。
确定性:如果 f(x)=0,则 x=0。
齐次性:对于所有 x∈R^n和t∈R,有 f(tx)=∣t∣f(x)。
三角不等式:对于所有 x,y∈R^n,有 f(x+y)≤f(x)+f(y)。
我们使用记号 f(x)=∥x∥,这表明范数是对实数绝对值的推广。范数可以看作是向量 x∈R^n的长度的度量:如果 ∥⋅∥是一个范数,则两个向量 (x,y)∈R^n之间的距离可以通过 ∥x−y∥来衡量。
示例:欧几里得范数(ℓ2)定义为:
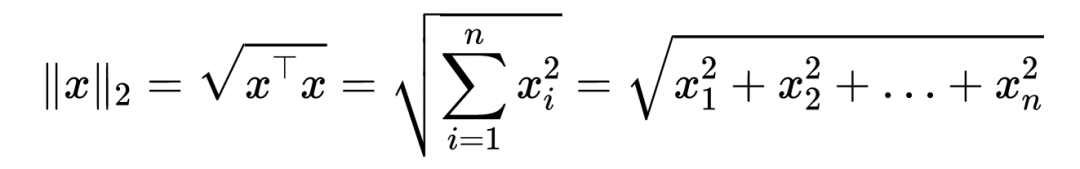
类似地,绝对值和范数(ℓ1)定义为:
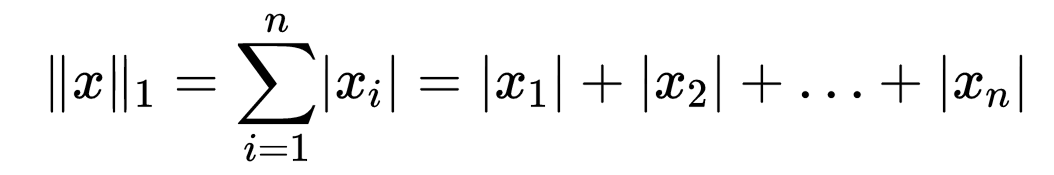
而切比雪夫范数(ℓ∞)定义为:
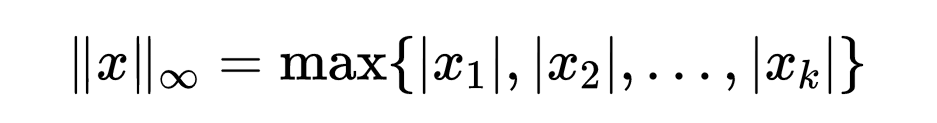
更一般地,对于 p⩾1,向量的闵可夫斯基范数(ℓp)定义为:
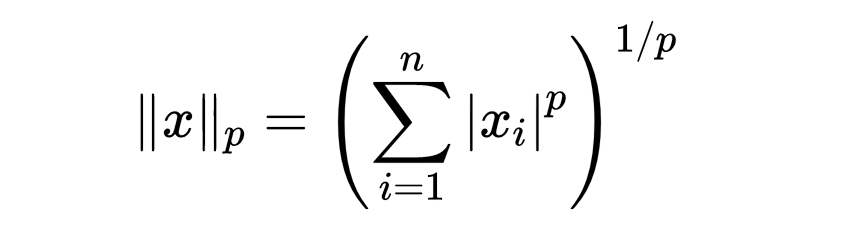
对于 p=1和 p=2,闵可夫斯基范数正是上面定义的 ℓ1和 ℓ2范数。闵可夫斯基范数也可以为 p∈(0,1]定义;然而,对于 p∈(0,1],它严格来说不是范数,因为它不满足三角不等式。给定范数 k⋅k的单位球是集合:
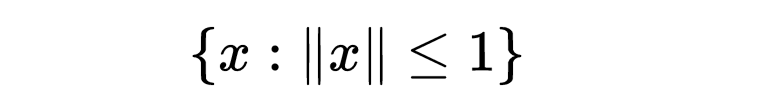
下图展示了不同范数在 R^2中的单位球。对于 p=2,单位球是一个圆(对于 n=3是一个球体),而对于 p=1,单位球是一个正方形(对于 n=3是一个立方体)。该图还展示了,当 p 趋于无穷大 时,ℓp 范数趋于ℓ1 范数。
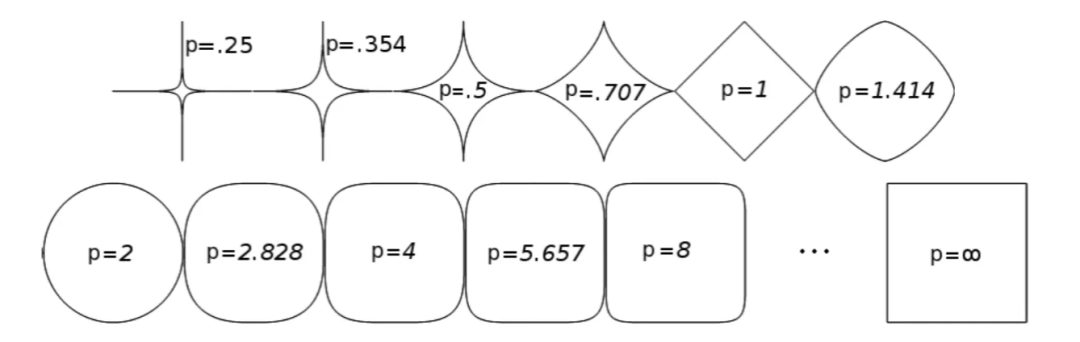
以上所有的 Rn范数是等价的,这意味着下面定义的收敛性、函数连续性等都不依赖于特定范数。例如,如果一个序列相对于一个范数收敛到一个固定点,那么对上述所有范数而言,收敛性都成立。
线性代数在机器学习中的应用
线性代数在机器学习中至关重要。它为理解数据表示和变换提供了基础,对于开发和优化机器学习模型至关重要。让我们深入探讨基本概念及其实际应用。
基本概念:向量、矩阵及运算
向量
向量是一个包含多个数值的数组,表示大小和方向。向量可以表示空间中的数据点。例如,3D 空间中的一个向量为:
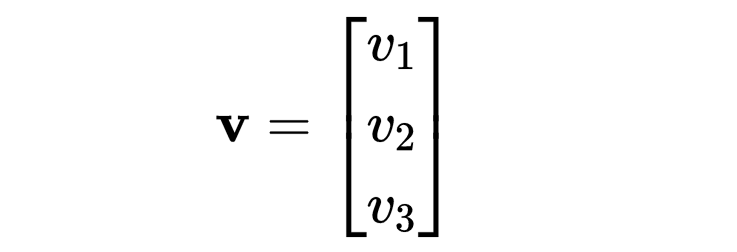
向量表示数据集的特征,其中每个元素对应一个特定的特征。
矩阵
矩阵是一个由数值组成的数组,表示为行列的网格。它可以看作是向量的集合,其中矩阵的每一行都是一个向量。矩阵可以表示数据集、变换等。例如,一个有 m 行 n 列的矩阵表示如下:

在机器学习中,矩阵表示整个数据集,其中行是数据点(即样本),列是特征。
矩阵运算
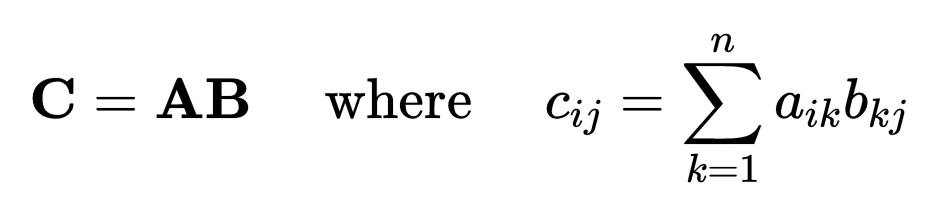

注意,与上面的矩阵 A 相比,行和列的索引发生了交换。
特征值和特征向量
特征值和特征向量是理解线性变换的基础。给定一个方阵 A,那么特征向量 v 和对应的特征值 λ 满足以下方程:
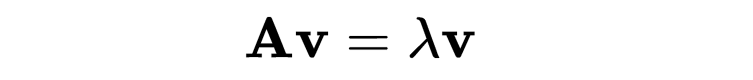
想象你在一片草地上推一辆手推车。
手推车的滚动方向就是特征向量;
手推车的加速或减速幅度就是特征值;
而方阵就是描述手推车上的力的一种数学表示。
这个方程通过 A 变换 v,得到的是 v 的一个缩放版本。特征值和特征向量常用于机器学习算法中,如主成分分析(PCA)。
主成分分析(PCA)就像一种数据“压缩技术”,它帮助我们从复杂的高维数据中找出最重要的“特征”,即差异最大的方向或变化最明显的部分,然后用更少的维度来简化和表示这些数据,确保在减少数据复杂度的同时,保留尽可能多的重要信息。
矩阵分解与降维
主成分分析(PCA)是一种降维技术,它将数据转换到一个新的坐标系,其中最大方差位于前几个坐标(即主成分)上。该算法的步骤如下:
标准化数据:对每个特征减去均值并除以标准差。
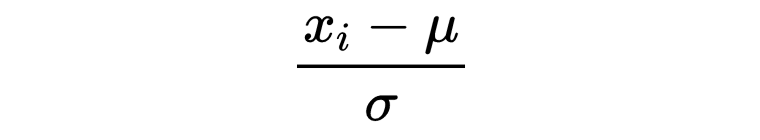
计算协方差矩阵:
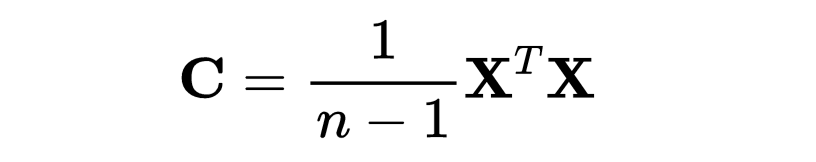
协方差是用来衡量两个变量之间关系的一种统计量。通俗地说,协方差告诉我们,当一个变量发生变化时,另一个变量是如何随之变化的。
如果两个变量在协方差计算中表现为正数,这意味着当一个变量增加时,另一个变量也倾向于增加,反之亦然。这叫做正相关。
如果协方差是负数,则意味着当一个变量增加时,另一个变量倾向于减少,反之亦然。这叫做负相关。
如果协方差接近零,则表示两个变量之间没有明显的线性关系,它们的变化是独立的。
计算协方差矩阵的特征值和特征向量。方差最大的轴的方向在特征向量中,方差的量(即大小)在特征值中。
按特征值递减顺序排序特征向量,并选择前 k 个特征向量。因此,前 k 个特征值捕捉到最大的方差。
使用选择的特征向量对数据进行变换。
奇异值分解(SVD)是一种矩阵分解技术,它将矩阵 A 分解为三个矩阵:
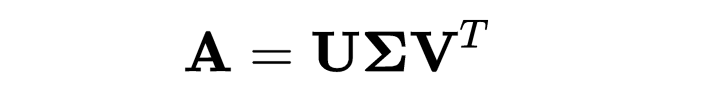
其中,U 和 V 是正交矩阵,Σ 是奇异值的对角矩阵。SVD 用于推荐系统、潜在语义分析等。
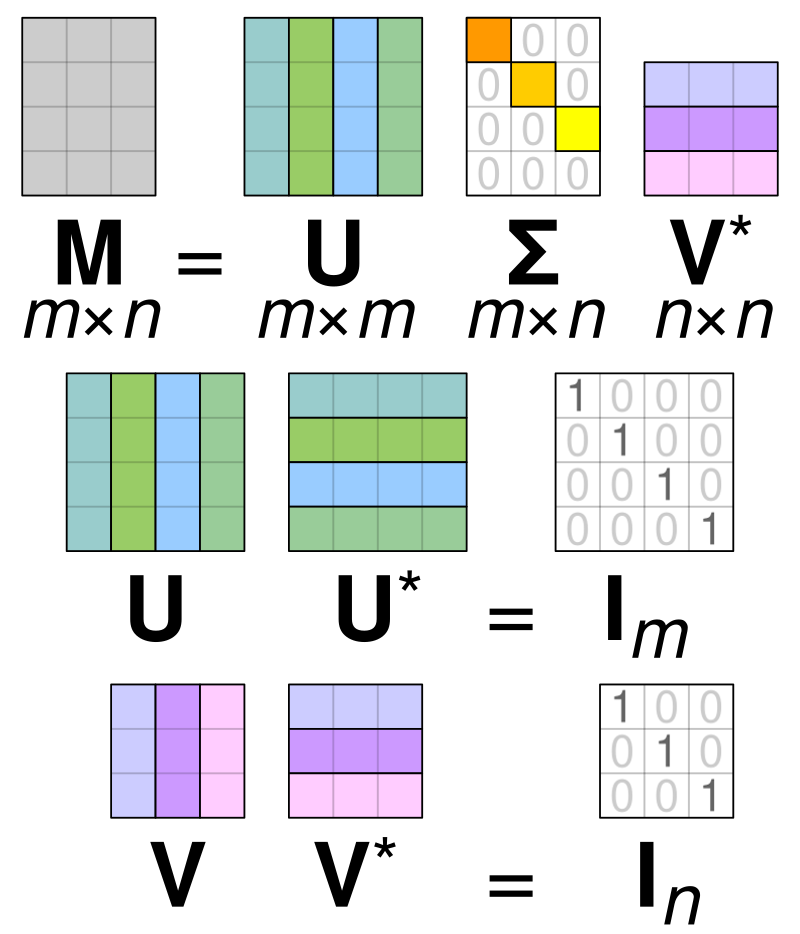
因此,它将任何线性变换分解为三个几何变换的组合。具体来说,首先是一个旋转(或反射)V,然后是按坐标逐一进行的缩放 Σ,最后再进行另一个旋转(或反射)。
实际应用
主成分分析(PCA) 降低数据集的维度,同时保留尽可能多的方差。这使得数据更容易可视化并降低计算成本。
import numpy as npfrom sklearn.decomposition import PCAimport matplotlib.pyplot as plt
# Generate synthetic datanp.random.seed(0)data = np.random.randn(100, 5)# Standardize the datadata -= np.mean(data, axis=0)# Apply PCApca = PCA(n_components=2)data_pca = pca.fit_transform(data)# Plot the resultsplt.scatter(data_pca[:, 0], data_pca[:, 1])plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')plt.title('PCA on Synthetic Data')plt.show()
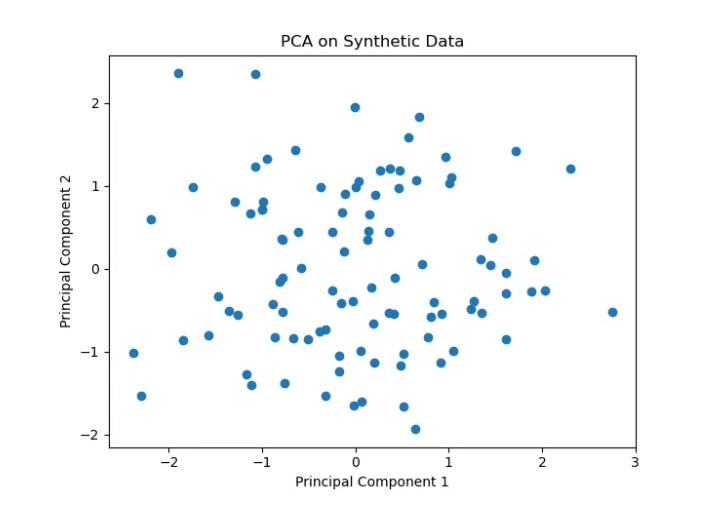
奇异值分解(SVD) 用于推荐系统中预测用户偏好。
import numpy as npfrom scipy.sparse.linalg import svds
# Example user-item rating matrix
R = np.array([ [5, 3, 0, 1], [4, 0, 0, 1], [1, 1, 0, 5], [1, 0, 0, 4], [0, 1, 5, 4],])*1.0
# Apply SVDU, sigma, Vt = svds(R, k=2)sigma = np.diag(sigma)# Predict ratingspredicted_ratings = np.dot(np.dot(U, sigma), Vt)print(predicted_ratings)
输出:
[[ 5.13406479 1.90612125 -0.72165061 1.5611261 ]
[ 3.43308995 1.28075331 -0.45629689 1.08967559]
[ 1.54866643 1.0449763 1.78873709 3.96755551]
[ 1.17598269 0.80359806 1.40136891 3.08786154]
[-0.44866693 0.5443561 3.09799526 5.15263893]]
微积分在机器学习中的应用
微积分在理解和优化机器学习模型中起着至关重要的作用。它为分析和改进算法提供了工具,尤其是在优化方面。
基本概念:导数与积分
导数测量函数随着输入变化而变化的程度。它是微积分中的基本概念,对于理解机器学习中的优化至关重要。函数 f(x)相对于x的导数记为 f′(x)或
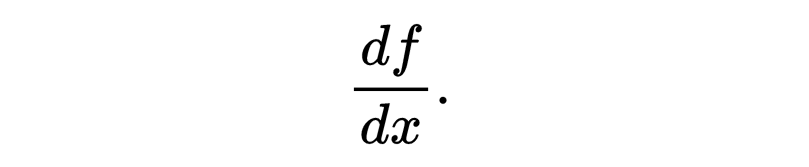
例如,函数 f(x)的导数为:
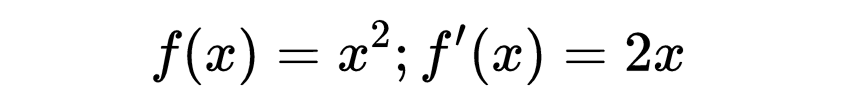
积分测量曲线下的面积。在机器学习中,积分的使用比导数少,但在理解分布和概率模型时可能很重要。函数 f(x)在区间 [a, b] 上的积分记为:
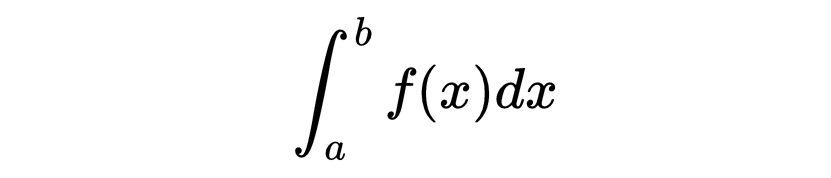
偏导数和梯度
偏导数用于处理多变量函数。它测量当一个输入变量变化时,函数的变化程度,而其他变量保持不变。函数 f(x,y)相对于x的偏导数记为:
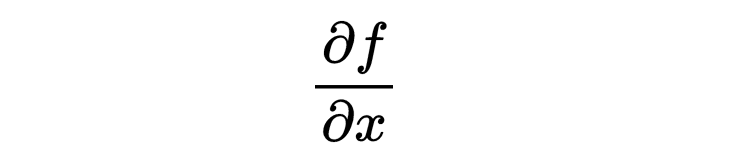
例如,如果
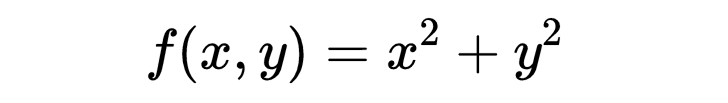
那么:
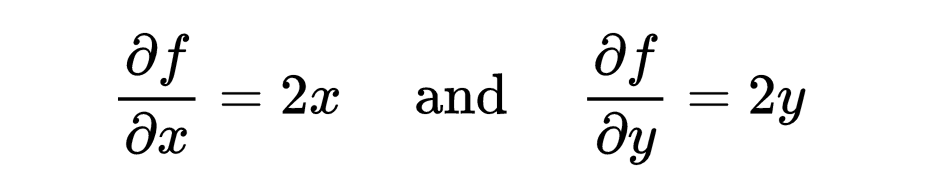
梯度是偏导数的向量,指向函数最陡的增加方向。对于函数 f(x,y),梯度记为 ∇f并表示为:
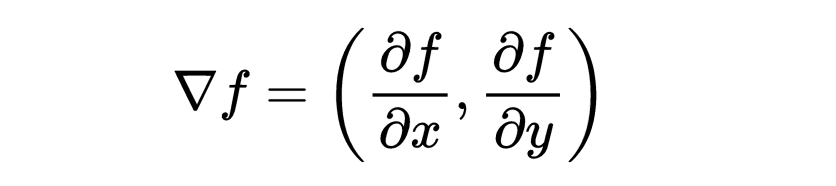
更一般地,任意向量值函数的梯度如下所示。
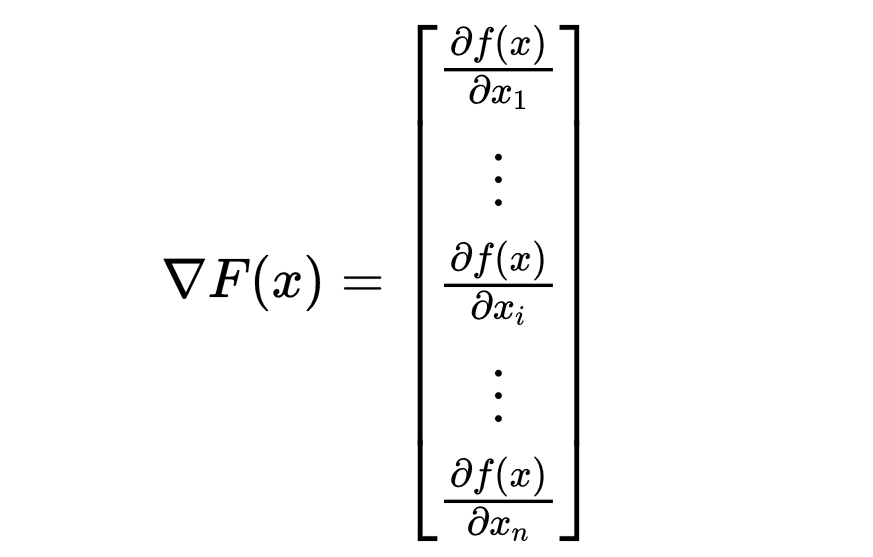
在机器学习中,梯度用于优化,通过在负梯度方向上更新模型参数以最小化损失函数。
示例:
证明二次函数
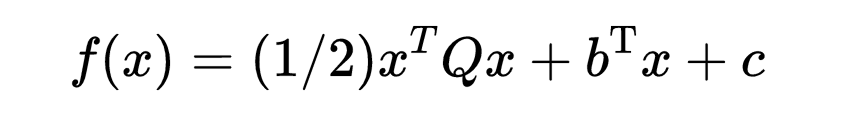
的梯度为
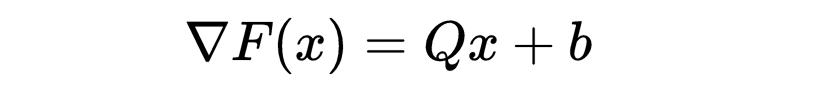
在点x_0处,函数f的泰勒展开式为:
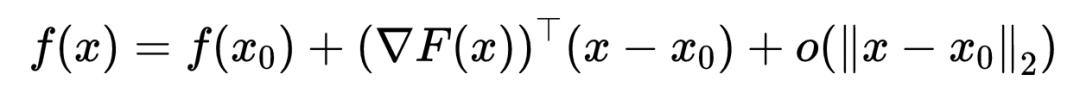
因此,仿射函数
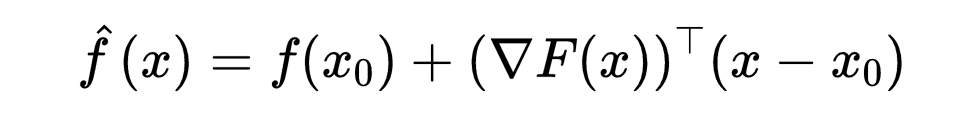
可以写成以下向量内积形式(设z = f (x)):
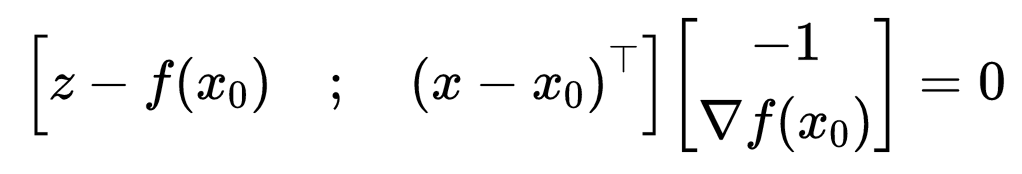
换句话说,方程 (1) 定义了一个通过一个点的超平面:
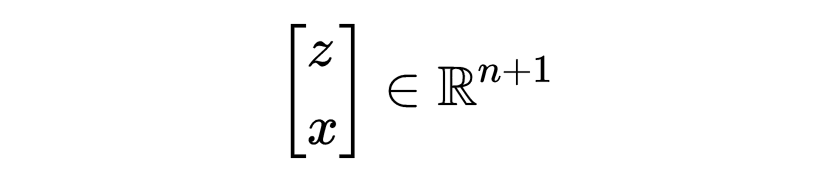
这个点是:
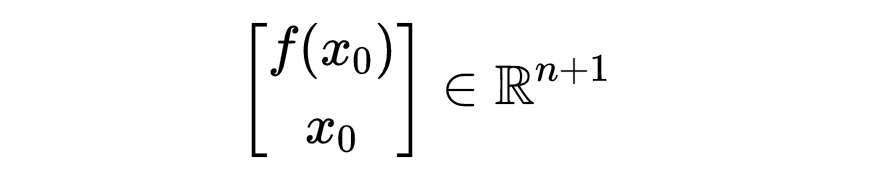
超平面的法线由以下公式给出:
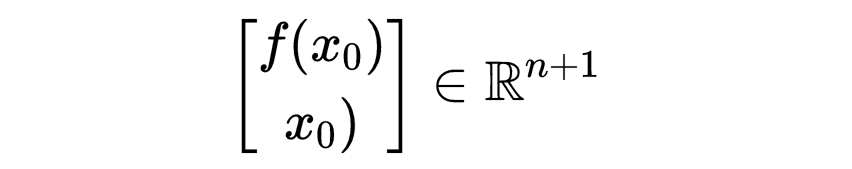
这一点在下图中得到了说明。
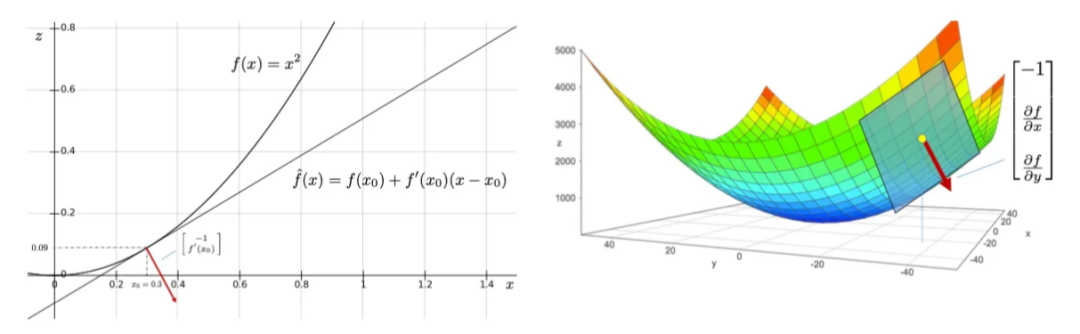
让我们进一步理解梯度的物理意义。梯度在 x_0∈R^d处垂直于由
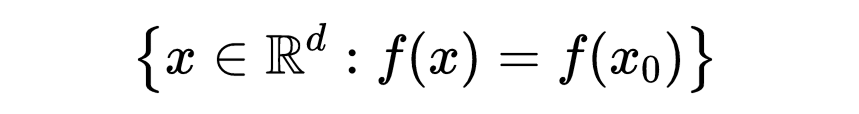
定义的等高线。此外,∇f(x_0)指向最陡上升的方向:沿着梯度方向将导致f在x_0附近的最大可能增加。下图展示了这一点。
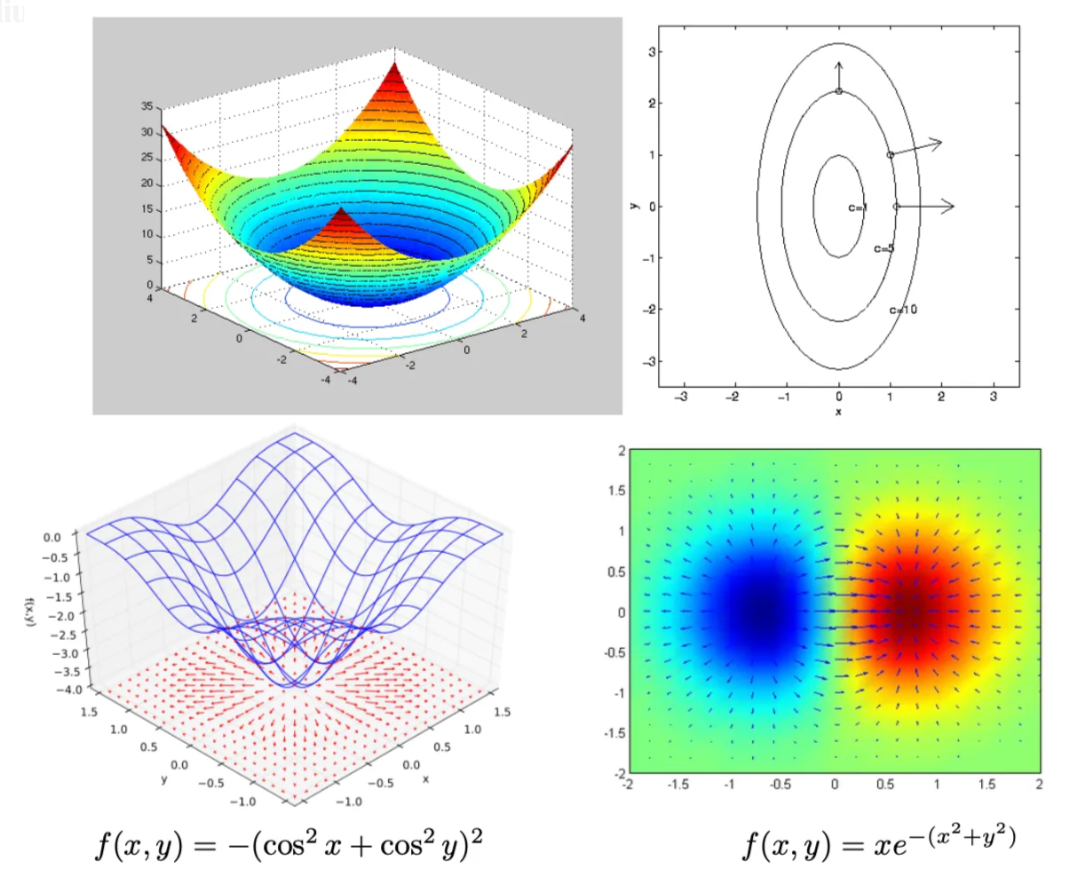
链式法则和反向传播
链式法则是微积分中的一个基本定理,用于计算复合函数的导数。如果函数z依赖于y,而y依赖于 x,那么 z 相对于x 的导数为:
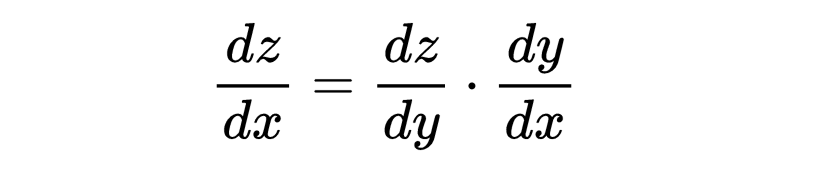
例如,如果 z=f(y)且 y=g(x),那么:
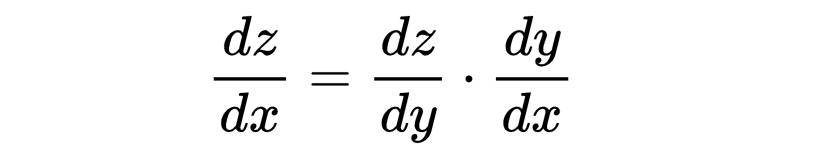
反向传播是一种用于训练神经网络的算法。它使用链式法则计算损失函数相对于网络中每个权重的梯度。这允许通过更新权重来最小化损失。
反向传播的步骤如下:
前向传播:计算网络的输出。
计算损失:计算预测值与实际值之间的损失。
反向传播:使用链式法则计算损失相对于每个权重的梯度。
更新权重:使用梯度调整权重以最小化损失。
实际应用
梯度下降 是一种优化算法,通过迭代地向最陡下降方向(即负梯度方向)移动来最小化损失函数。
梯度下降算法:
随机初始化参数(权重)。
计算损失函数相对于参数的梯度。
以步长(学习率)的大小在梯度的相反方向上更新参数。
重复步骤 2 和 3,直到收敛。
数学上,梯度下降的参数更新规则为:
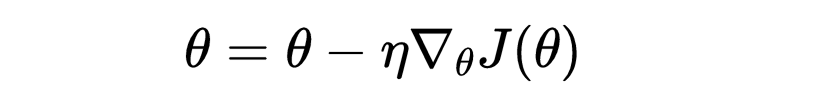
其中:

实际示例:梯度下降
import numpy as np
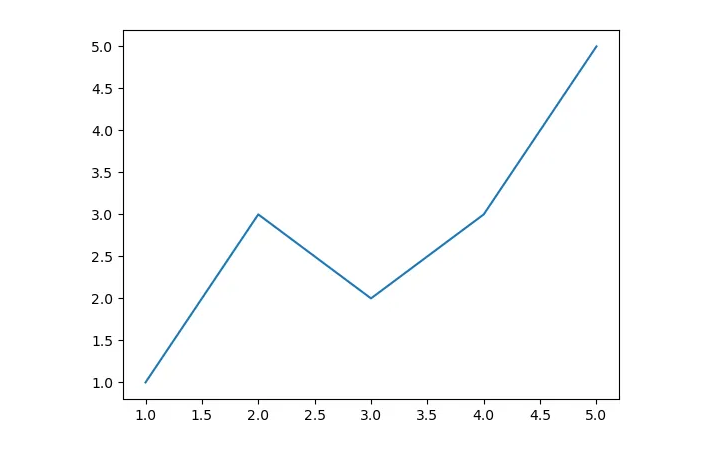
# Example dataX = np.array([1, 2, 3, 4, 5])y = np.array([1, 3, 2, 3, 5])# Parametersm = 0b = 0learning_rate = 0.01epochs = 1000# Gradient descentfor _ in range(epochs): y_pred = m * X + b dm = -2 * np.sum((y - y_pred) * X) / len(X) db = -2 * np.sum(y - y_pred) / len(X) m -= learning_rate * dm b -= learning_rate * dbprint(f"Optimized parameters: m = {m}, b = {b}")
输出:
优化后的参数:m = 0.8015522329369132, b = 0.3943959465768995
我们再尝试使用 1000 次迭代。
输出:
优化后的参数:m = 0.8000000000000033, b = 0.39999999999998903
注意:该解逐渐接近其近似的数值结果,y 截距为 0.4,斜率 m 为 0.8。下图展示了这一近似情况。
线性代数和微积分在模型训练中的应用
线性代数和微积分是训练机器学习模型不可或缺的工具。这些数学概念支撑了模型从数据中学习、优化参数并进行预测的操作。
线性代数在模型训练中的应用
数据表示:如前所述,数据集通常表示为矩阵,其中每一行代表一个数据点(即样本),每一列代表一个特征。例如,包含 m 个数据点和 n 个特征的数据集描述为一个 m×n 的矩阵 XXX。
线性变换:在许多模型中(如线性回归),预测值是输入特征的线性组合。这可以表示为矩阵乘法:y=Xw,其中 y是预测值向量,X是输入矩阵,w是权重向量。
矩阵分解:如主成分分析(PCA)等技术使用特征值和特征向量来减少数据的维度,使模型训练和数据可视化更容易。奇异值分解(SVD)用于推荐系统,将用户-物品交互矩阵分解为潜在因素。
微积分在模型训练中的应用
优化:微积分,特别是导数,用于最小化损失函数。损失函数相对于模型参数的梯度指示参数应如何更新以减少误差。
梯度下降:这是一种迭代优化算法,用于最小化损失函数。它依赖于计算损失函数相对于参数的梯度(偏导数),并在负梯度方向上更新参数。
反向传播:在神经网络中,反向传播利用链式法则计算损失函数相对于每个权重的梯度。这允许有效地计算所需的更新以最小化损失。
使用这些数学概念进行模型优化的示例
示例 1:使用梯度下降进行线性回归
线性回归旨在找到最适合数据点的线,通过最小化预测值与实际值之间的均方误差(MSE)来实现。
数学公式:
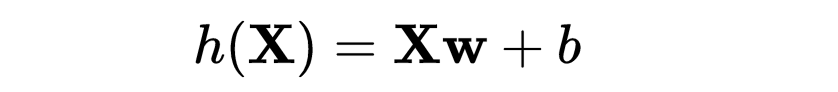
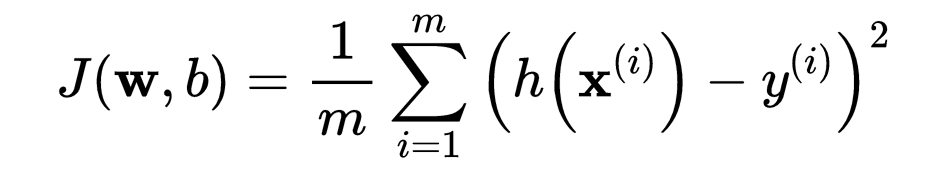
使用梯度下降更新权重 w 和偏差 b:
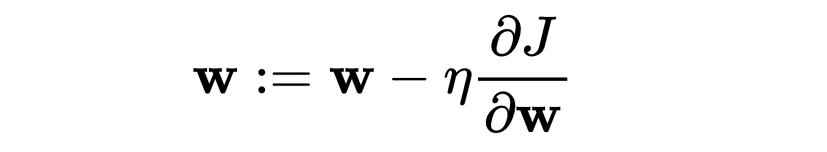
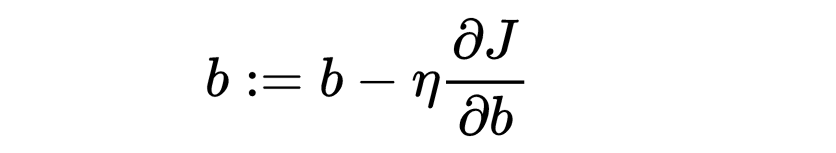
import numpy as np
# Example dataX = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)y = np.array([1, 3, 2, 3, 5])# Add a column of ones to include the bias term in the weight vectorX_b = np.c_[np.ones((X.shape[0], 1)), X]# Parameterslearning_rate = 0.01n_iterations = 1000m = len(y)# Initialize weightstheta = np.random.randn(2, 1)# Gradient Descentfor iteration in range(n_iterations): gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y.reshape(-1, 1)) theta -= learning_rate * gradientsprint(f"Optimized parameters: {theta.ravel()}")
输出:
优化后的参数:[0.38853948 0.80317438]
注意,以上 X 的翻转使得 m 和 b 的近似值与前面的梯度下降示例相比有所不同。
示例 2:使用反向传播进行神经网络训练
神经网络使用反向传播算法进行训练,该算法依赖于链式法则来高效计算梯度。
数学公式:
前向传播:计算网络的输出。
计算损失:计算损失(如分类的交叉熵损失)。
反向传播:使用链式法则计算损失相对于每个权重的梯度。
更新权重:使用计算出的梯度更新权重。
import torchimport torch.nn as nnimport torch.optim as optim
# Define a simple neural networkclass SimpleNN(nn.Module):def __init__(self): super(SimpleNN, self).__init__() self.fc1 = nn.Linear(2, 3) self.fc2 = nn.Linear(3, 1)
def forward(self, x): x = torch.relu(self.fc1(x)) x = torch.sigmoid(self.fc2(x))return x# Example dataX = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])y = torch.tensor([[0.0], [1.0], [1.0], [0.0]])# Initialize model, loss function, and optimizermodel = SimpleNN()criterion = nn.BCELoss()optimizer = optim.SGD(model.parameters(), lr=0.1)# Training loopfor epoch in range(10000): optimizer.zero_grad() output = model(X) loss = criterion(output, y) loss.backward() optimizer.step()print("Finished Training")print(output)
输出:
训练结束
tensor([[0.0259],
[0.8772],
[0.8772],
[0.1237]], grad_fn=)
注意,X 的输出值逐渐接近 y 的真实值。
案例研究和实际示例
线性代数和微积分在开发和优化机器学习模型中至关重要的真实世界示例
线性代数和微积分是许多成功的机器学习应用的基础。让我们探索一些实际的例子,了解这些数学工具如何在模型开发和优化中发挥关键作用。
图像识别中的卷积神经网络(CNNs)
线性代数广泛用于支持 CNN 的卷积操作中。通过反向传播,微积分用于优化网络,通过更新权重来最小化损失函数。
自然语言处理(NLP)中的词嵌入
像 word2vec 这样的技术使用矩阵分解来捕捉词之间的关系。基于微积分的优化算法(如梯度下降)用于训练这些模型。
推荐系统
奇异值分解(SVD)对用户-物品交互矩阵进行分解。这种分解使系统能够预测用户尚未评分的物品的偏好。
自动驾驶
自动驾驶汽车的目标检测和路径规划的机器学习模型在数据表示和变换中严重依赖于线性代数。微积分用于优化和控制算法。
具体应用的逐步演练
让我们深入探讨两个详细的示例:使用SVD构建推荐系统和训练CNN进行图像分类。
示例 1:使用SVD的推荐系统
我们将上述示例分解为可理解的步骤。
步骤 1:数据准备
我们从一个用户-物品评分矩阵开始,其中行代表用户,列代表物品。矩阵中的条目是用户对物品的评分。
import numpy as np
# Example user-item rating matrixR = np.array([ [5, 3, 0, 1], [4, 0, 0, 1], [1, 1, 0, 5], [1, 0, 0, 4], [0, 1, 5, 4],])*1.0
步骤 2:应用SVD
我们将评分矩阵 R 分解为三个矩阵:
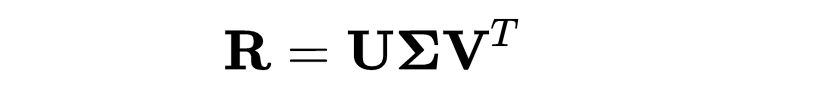
from scipy.sparse.linalg import svds
# Apply SVDU, sigma, Vt = svds(R, k=2)sigma = np.diag(sigma)print("U matrix:\n", U)print("Sigma matrix:\n", sigma)print("V^T matrix:\n", Vt)
输出:
U matrix:
[[-0.66924125 -0.43689593]
[-0.44308727 -0.29717498]
[ 0.13631518 -0.51589728]
[ 0.11077382 -0.39999635]
[ 0.5700326 -0.54282768]]
Sigma matrix:
[[6.22925557 0. ]
[0. 9.03171974]]
V^T matrix:
[[-0.78203025 -0.20891356 0.45754472 0.36801718]
[-0.47488998 -0.26234348 -0.3005118 -0.78444124]]
步骤 3:重构矩阵
我们使用分解后的矩阵重构原始矩阵R,以预测缺失的评分。
# Reconstruct the matrixR_pred = np.dot(np.dot(U, sigma), Vt)print("Predicted ratings:\n", R_pred)
输出:
Predicted ratings:
[[ 5.13406479 1.90612125 -0.72165061 1.5611261 ]
[ 3.43308995 1.28075331 -0.45629689 1.08967559]
[ 1.54866643 1.0449763 1.78873709 3.96755551]
[ 1.17598269 0.80359806 1.40136891 3.08786154]
[-0.44866693 0.5443561 3.09799526 5.15263893]]
步骤 4:评估模型
我们可以通过比较已知值的预测评分和实际评分来评估模型。
from sklearn.metrics import mean_squared_error
# Known ratingsknown_ratings = R[R.nonzero()]
predicted_ratings = R_pred[R.nonzero()]# Calculate Mean Squared Errormse = mean_squared_error(known_ratings, predicted_ratings)print("Mean Squared Error:", mse)
输出:
Mean Squared Error: 0.7111239245689356
示例 2:使用CNN进行图像分类
步骤 1:加载和预处理数据
我们将使用CIFAR-10数据集,这是一个流行的图像分类数据集。
import torchimport torchvisionimport torchvision.transforms as transforms
# Define transformationstransform = transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),])# Load datasetstrainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)trainloader = torch.utils.data.DataLoader(trainset, batch_size=100, shuffle=True)testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False)
步骤 2:定义CNN模型
我们定义一个简单的CNN模型,包含卷积层、池化层和全连接层。
import torch.nn as nnimport torch.nn.functional as F
class SimpleCNN(nn.Module):def __init__(self):super(SimpleCNN, self).__init__()self.conv1 = nn.Conv2d(3, 6, 5)self.pool = nn.MaxPool2d(2, 2)self.conv2 = nn.Conv2d(6, 16, 5)self.fc1 = nn.Linear(16 * 5 * 5, 120)self.fc2 = nn.Linear(120, 84)self.fc3 = nn.Linear(84, 10)def forward(self, x): x = self.pool(F.relu(self.conv1(x))) x = self.pool(F.relu(self.conv2(x))) x = x.view(-1, 16 * 5 * 5) x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x)return xnet = SimpleCNN()
步骤 3:定义损失函数和优化器
我们使用交叉熵损失和随机梯度下降(SGD)进行优化。
import torch.optim as optim
criterion = nn.CrossEntropyLoss()optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
步骤 4:训练模型
我们通过将数据传递给网络,计算损失,并使用反向传播更新权重来训练CNN。
for epoch in range(6): # Loop over the dataset multiple times running_loss = 0.0for i, data in enumerate(trainloader, 0): inputs, labels = data
optimizer.zero_grad() # Zero the parameter gradients
outputs = net(inputs) loss = criterion(outputs, labels) loss.backward() optimizer.step()
running_loss += loss.item()if i % 100 == 99: # Print every 100 mini-batches print(f"[{epoch + 1}, {i + 1}] loss: {running_loss / 100:.3f}") running_loss = 0.0
print("Finished Training")
输出:
[1, 100] loss: 2.304
[1, 200] loss: 2.303
[1, 300] loss: 2.304
[1, 400] loss: 2.302
[1, 500] loss: 2.301
[2, 100] loss: 2.299
[2, 200] loss: 2.297
[2, 300] loss: 2.295
[2, 400] loss: 2.293
[2, 500] loss: 2.288
Finished Training
步骤 5:评估模型
我们在测试数据集上评估训练后的CNN,以衡量其性能。
correct = 0total = 0with torch.no_grad():for data in testloader:images, labels = dataoutputs = net(images)_, predicted = torch.max(outputs.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()
print(f"Accuracy of the network on the 10000 test images: {100 * correct / total:.2f}%")
输出:
Accuracy of the network on the 10000 test images: 18.06%
随机猜测的准确率为10%,因为有十个类别。我们是否可以超过18.06%的准确率?当然可以,让我们继续训练。以下是继续训练相同模型六个额外周期的输出。
输出:
[1, 100] loss: 2.281
[1, 200] loss: 2.267
[1, 300] loss: 2.242
[1, 400] loss: 2.199
[1, 500] loss: 2.132
[2, 100] loss: 2.085
[2, 200] loss: 2.017
[2, 300] loss: 1.993
[2, 400] loss: 1.956
[2, 500] loss: 1.923
[3, 100] loss: 1.898
[3, 200] loss: 1.863
[3, 300] loss: 1.841
[3, 400] loss: 1.810
[3, 500] loss: 1.767
[4, 100] loss: 1.753
[4, 200] loss: 1.729
[4, 300] loss: 1.693
[4, 400] loss: 1.664
[4, 500] loss: 1.663
[5, 100] loss: 1.644
[5, 200] loss: 1.635
[5, 300] loss: 1.603
[5, 400] loss: 1.621
[5, 500] loss: 1.590
[6, 100] loss: 1.590
[6, 200] loss: 1.572
[6, 300] loss: 1.570
[6, 400] loss: 1.556
[6, 500] loss: 1.553
Finished Training
再进行六个周期的训练:
输出:
Accuracy of the network on the 10000 test images: 51.91%
有许多其他方法可以改善多层感知器,这些超出了本篇文章的范围。
结论
在本篇文章中,我们探讨了支撑机器学习的基础数学概念。
理解机器学习的数学基础不仅仅是理论上的练习;对于任何认真掌握这一领域的人来说,这都是一个实际的必要条件。原因如下:
模型开发:扎实的数学基础可以让你开发和改进新算法。你可以超越将机器学习模型视为黑盒的做法,开始根据自己的需求更好地定制模型。
优化:许多机器学习算法依赖于源自微积分的优化技术。理解这些原理可以让你更有效地调整模型,提高其性能。
数据处理:线性代数对于高效处理和操作数据至关重要。从数据预处理到模型评估,涉及矩阵和向量的操作在机器学习中无处不在。
故障排除:深入理解机器学习背后的数学可以帮助你更有效地诊断和解决问题。你可以识别出模型表现不佳的原因,并进行有针对性的调整。