
SymPy 是一个 Python 库,专注于符号计算,提供了处理数学表达式、方程和公式的工具。与数值计算库不同,SymPy 能够进行符号微分、积分、极限等运算,适用于代数运算、微积分和方程求解等。与传统的数值计算库(如 NumPy)不同,SymPy 主要用于处理数学表达式、方程和公式的符号计算,而不是进行数值计算。
它支持多项式运算、矩阵操作、特征值计算等线性代数功能,并能处理数论和组合数学中的问题。SymPy 还具备简化数学表达式的功能,并能绘制数学函数和图形。作为一个完全用 Python 实现的开源库,SymPy 易于集成到 Python 环境中,广泛应用于学术研究、教育以及需要符号计算的领域。
什么是 SymPy?
它是计算机代数系统(computer alegebra systems,CAS)的一部分:一个允许我们进行代数和数学计算的库。
主要功能:
安装SymPy
简化和展开
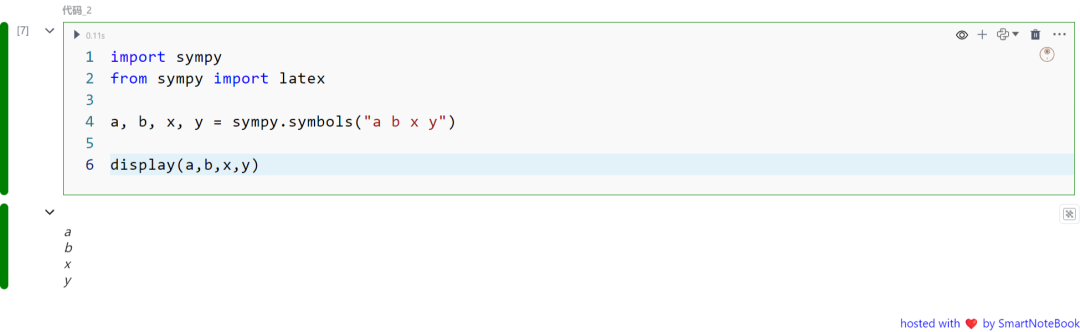
首先,导入 SymPy。然后定义 SymPy 变量,才能使用它们。通过创建 SymPy 的 symbols 来实现这一点。这些符号代表了数学变量:
import sympyfrom sympy import latex
a, b, x, y = sympy.symbols("a b x y")
display(a,b,x,y)
然后,我们可以构建表达式和方程:
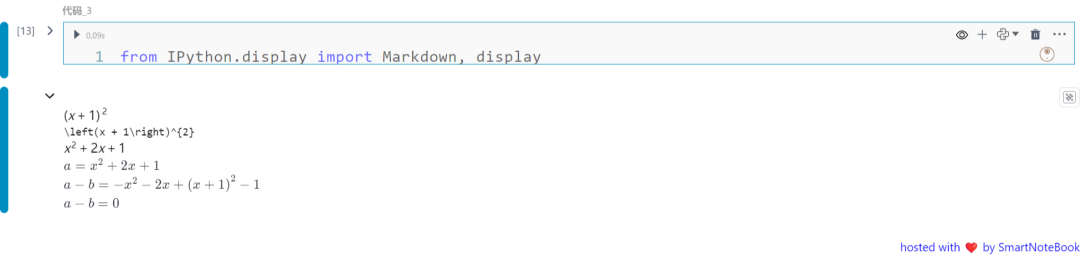
from IPython.display import Markdown, display
a = (x + 1)**2b = x**2 + 2*x + 1 display(a)print(latex(a)) display(b)
expanded = sympy.expand(a)display(Markdown(f"$a = {latex(expanded)}$"))
a_minus_b = a-bdisplay(Markdown(f"$a-b = {latex(a_minus_b)}$"))
display(Markdown(f"$a-b$ $= {latex(sympy.simplify(a_minus_b))}$"))
等式判断
我们可以测试两个表达式是否相同,方法如下:

变量赋值和评估
在定义了一个 SymPy 符号并将其分配给 Python 变量后,不能简单地给 Python 变量赋值。如果这样做,变量将不再是一个符号。相反,你需要使用 subs() 方法将值与 SymPy 符号关联起来:
x, y = sympy.symbols("x y")expr = x+yresult = expr.subs({x: 2, y: 5})print(f"{expr=}, {result=}")

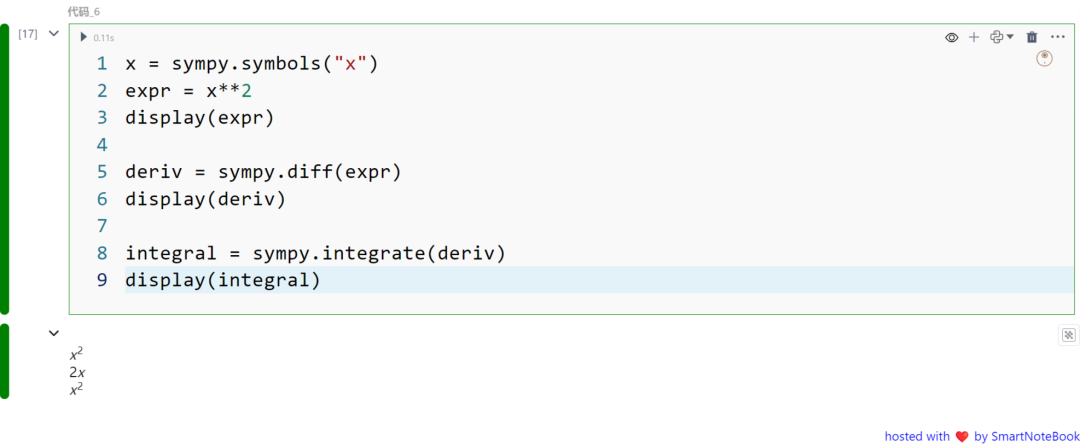
微分和积分
在 SymPy 中,积分和微分非常简单:
x = sympy.symbols("x")
expr = x**2display(expr)
deriv = sympy.diff(expr)display(deriv)
integral = sympy.integrate(deriv)display(integral)
求解二次方程
求解二次方程很简单,只需提供二次方程的系数,然后运行 SymPy 的 solve() 函数即可:
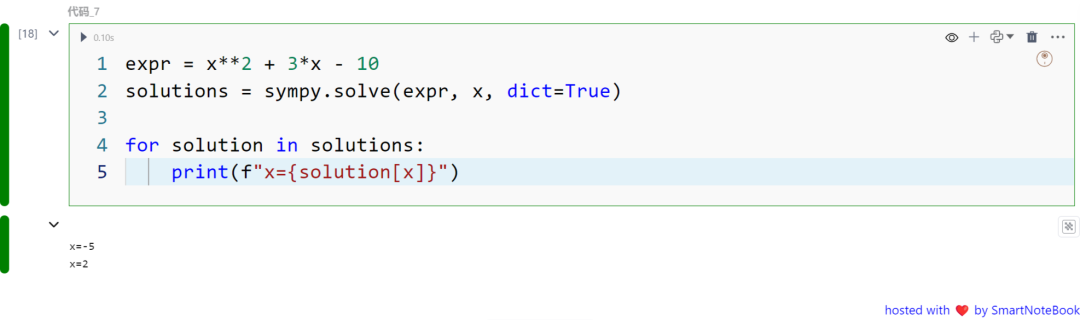
expr = x**2 + 3*x - 10solutions = sympy.solve(expr, x, dict=True)
for solution in solutions: print(f"x={solution[x]}")
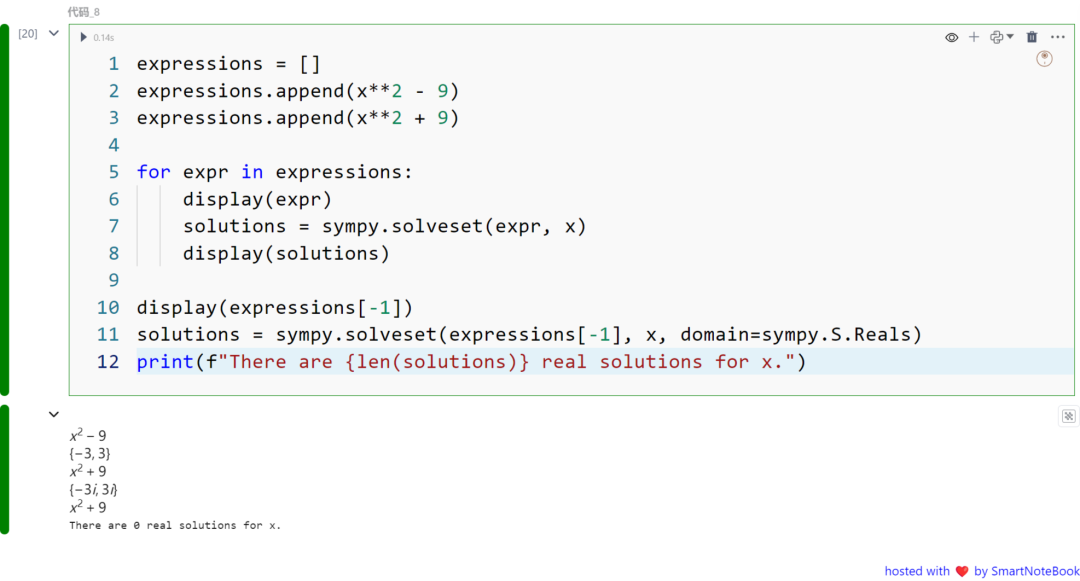
有时,我们只希望看到实数解,而不是复数解。(复数解是包含虚数部分的解,即以负数平方根表示的解。)在这种情况下,我们可以使用 solveset() 并指定仅允许实数的域。例如:
expressions = []expressions.append(x**2 - 9) expressions.append(x**2 + 9)
for expr in expressions: display(expr) solutions = sympy.solveset(expr, x) display(solutions)
display(expressions[-1])solutions = sympy.solveset(expressions[-1], x, domain=sympy.S.Reals)print(f"There are {len(solutions)} real solutions for x.")
转换为数值
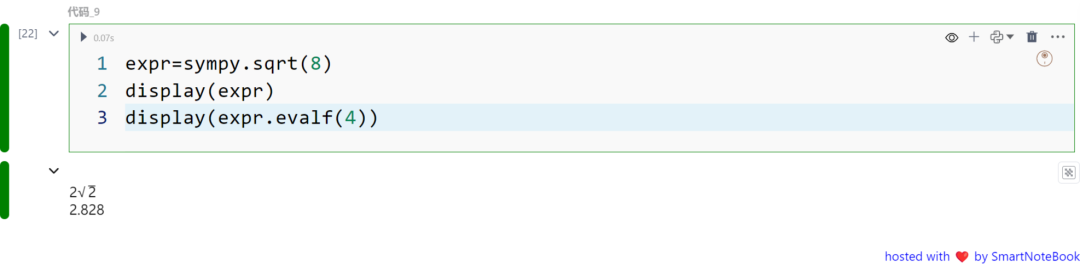
SymPy 返回的结果是精确的数学符号。但有时我们希望将这些结果转换为数值表示,可以使用evalf 函数。示例如下:
expr=sympy.sqrt(8)display(expr)display(expr.evalf(4))
绘制图形
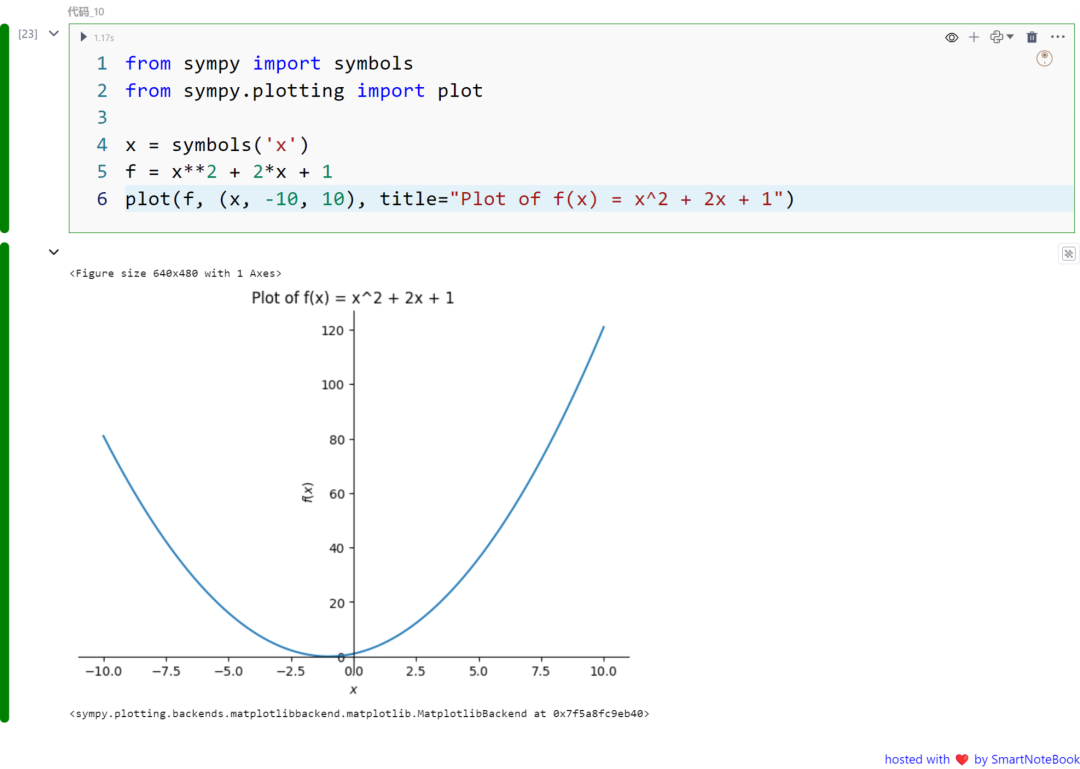
使用 SymPy 绘制图形使用 SymPy 的 plot 函数,支持函数、隐函数和参数方程,下面是小几个例子。
from sympy import symbolsfrom sympy.plotting import plot
x = symbols('x')f = x**2 + 2*x + 1plot(f, (x, -10, 10), title="Plot of f(x) = x^2 + 2x + 1")
from sympy import symbolsfrom sympy.plotting import plot
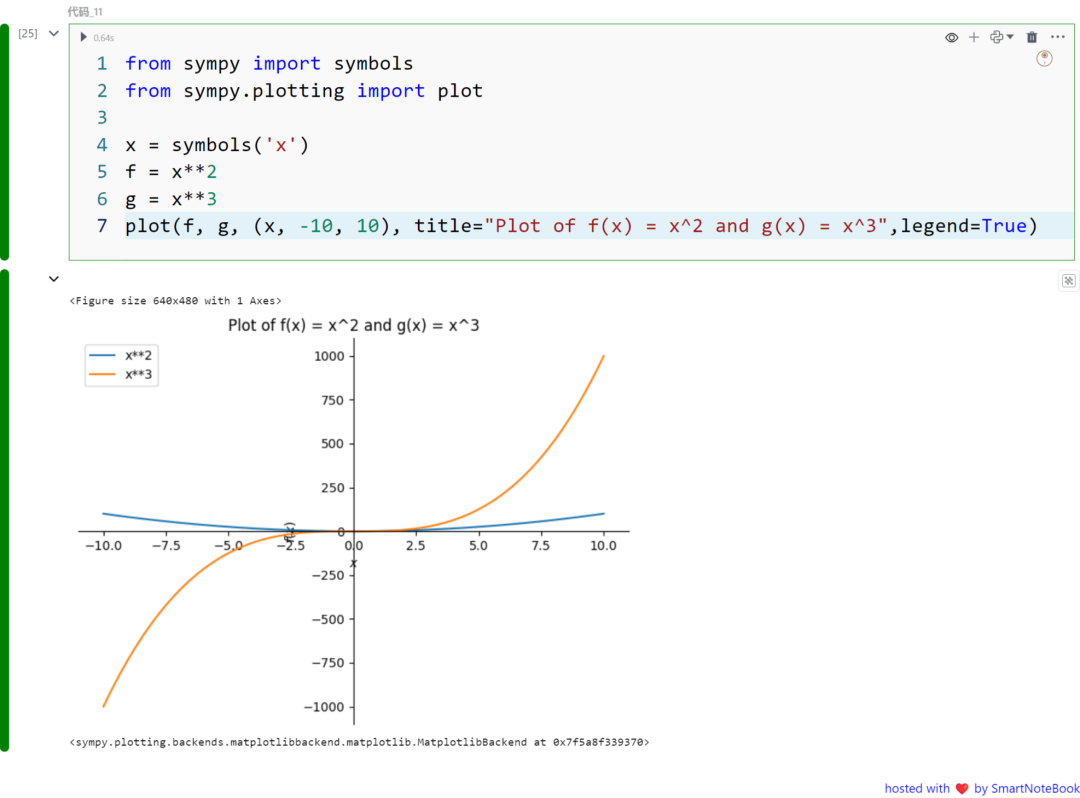
x = symbols('x')f = x**2g = x**3plot(f, g, (x, -10, 10), title="Plot of f(x) = x^2 and g(x) = x^3",legend=True)
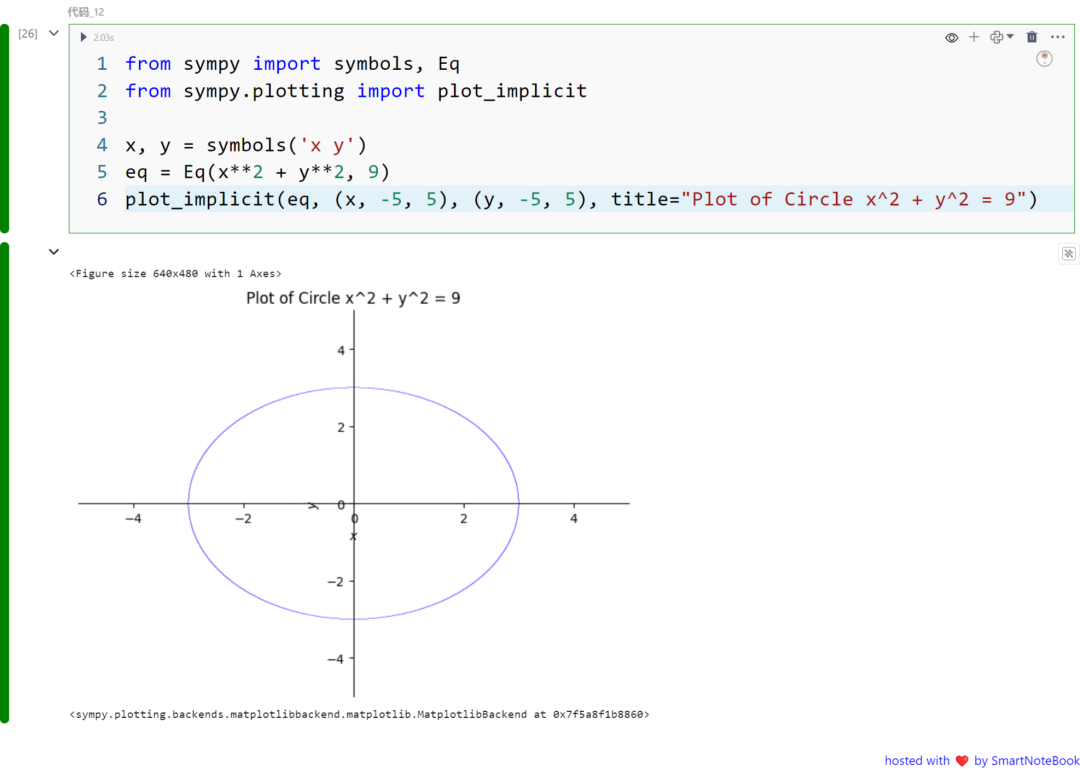
from sympy import symbols, Eqfrom sympy.plotting import plot_implicit
x, y = symbols('x y')eq = Eq(x**2 + y**2, 9)plot_implicit(eq, (x, -5, 5), (y, -5, 5), title="Plot of Circle x^2 + y^2 = 9")
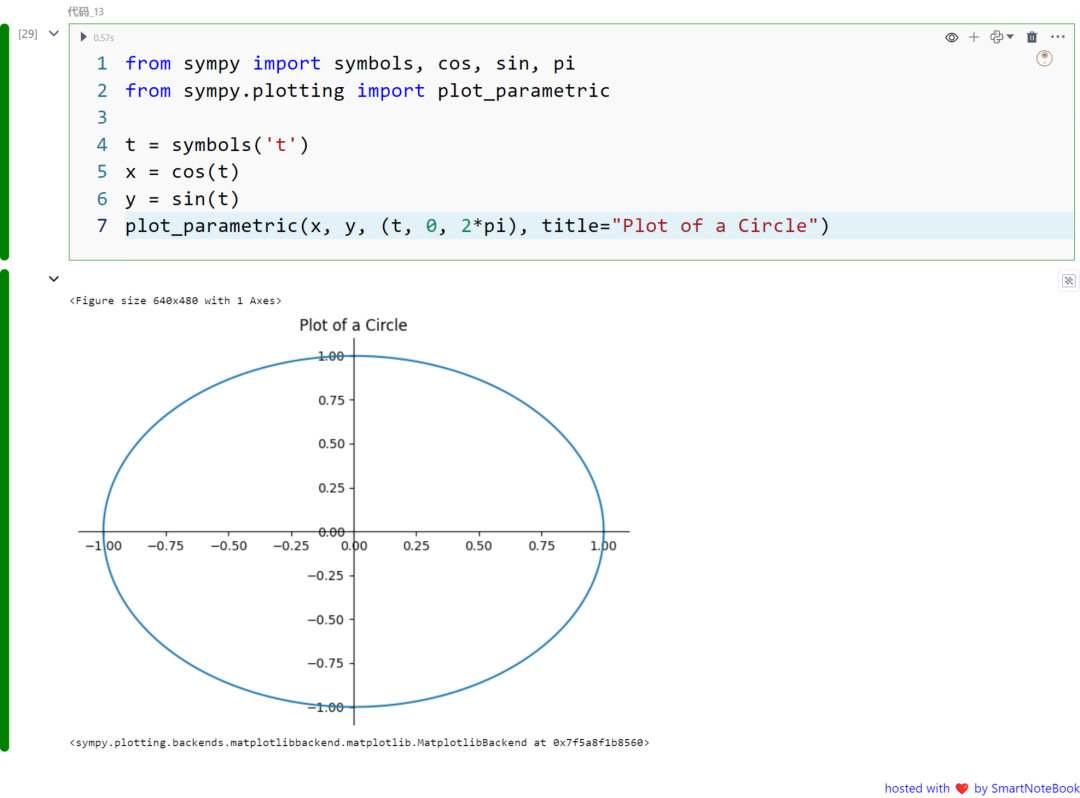
from sympy import symbols, cos, sin, pifrom sympy.plotting import plot_parametric
t = symbols('t')x = cos(t)y = sin(t)plot_parametric(x, y, (t, 0, 2*pi), title="Plot of a Circle")
SymPy 非常适合需要代数运算的问题。它可以用于求解复杂的方程和进行微积分运算。这里提供了一个快速入门的概述,并展示了一些使用 SymPy 的简单例子。