图中第二行就是卷积与反卷积的示意图,下面通过一个简单的例子来解释上图的内容。假设有4x4大小的二维矩阵D,有3x3大小的卷积核C,图示如下:
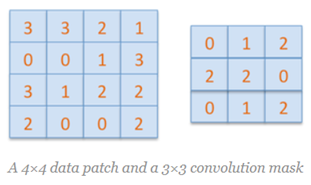
直接对上述完成卷积操作(不考虑边缘填充)输出卷积结果是2x2的矩阵

其中2x2卷积的输出结果来自D中第二行第二列像素位置对应输出,相关的卷积核与数据点乘的计算为:
0x3+1x3+2x2+2x0+2x0+0x1+0x3+1x1+2x2=12,可以看出卷积操作是卷积核在矩阵上对应位置点乘线性组合得到的输出,对D=4x4大小的矩阵从左到右,从上到下,展开得到16个维度的向量表示如下:
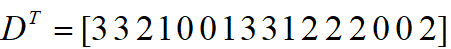
我们同样可以把3x3的卷积核表示如下:
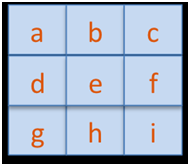
为了获得卷积核的4x4的向量表示,我们可以对其余部分填充零,那么卷积核在D上面移动的位置与对应的一维向量表示如下:
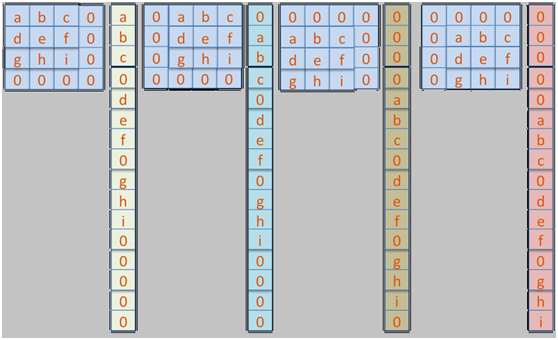
考虑到卷积核C与D的点成关系,合并在一起还可以写成如下形式:
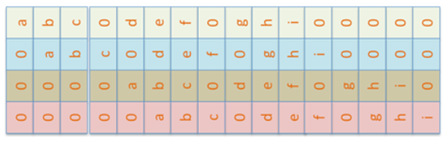
把上面卷积核中的字符表示替换为实际卷积核C,得到:

所以上述的卷积操作可以简单的写为:
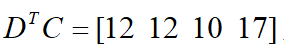
重排以后就得到上面的2x2的输出结果。
什么!还不明白,那我最后只能放一个大招了!我搞了个一维的转置卷积的例子:
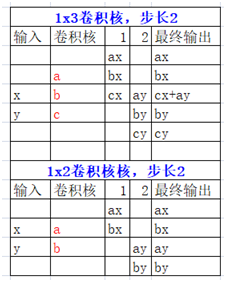
有个前提,你得先理解什么是卷积跟一维卷积,二维卷积等基本概念。这个例子就很直接,我用Excel绘制的,先看图:
解释一下,一维卷积的本来是1xN,转置变为Nx1的,然后同样用输入的数据跟卷积核点乘,点成的方式如上,如果有重叠的部分,就加在一起就好啦,这部分还可以通过代码来验证演示一波,pytorch的代码演示如下:
你好
from __future__ import print_function
import torch
import numpy as np
# 输入一维数据
d = torch.tensor([1.,2.])
# 一维卷积核
f = torch.tensor([3.0,4.0])
# 维度转换dd
d = d.view(1,1,2)
f = f.view(1,1,2)
# 一维转置卷积
ct1d = torch.nn.ConvTranspose1d(in_channels=1, out_channels=1, kernel_size=2, stride=2, bias=0)
ct1d.weight = torch.nn.Parameter(f);
# 打印输出
print("输入数据:", d)
print("输出上采样结果:", ct1d(d))
运行结果如下:

根据我的手绘Excel图,可以认为:
[x, y] = [1, 2],卷积核[a, b] = [3, 4],输出结果[ax, bx, ay, by] = [3, 4, 6, 8]
这个就是转置卷积上采样!这下还不明白我真的没法啦!
参考:
https://iksinc.online/2017/05/06/deconvolution-in-deep-learning/
2015 ICCV论文《Learning Deconvolution Network for Semantic Segmentation》