
今天是3月14日,是圆周率日(π日)。作为数据和Python从业者,我们以一种独特的方式纪念这个特殊的日子——通过整理下几个使用Python计算π的朴素方案。这不仅是对数学的致敬,也是对Python编程的致敬。
在庆祝π日的今天(3月14日),我们将通过四种不同的方法展示计算π的方式。这些方法分别是逼近法、蒙特卡罗方法、莱布尼兹公式和Chudnovsky算法。每种方法都有其独特的原理和逼近π的方式,让我们一起来探索这些方法的奥秘,并感受数学之美与编程的魅力。
逼近法
逼近法通过将多边形(逐步提升多边形的边数)的边长逼近成圆的周长,从而逼近π的值。这是一种直观且易于理解的方法。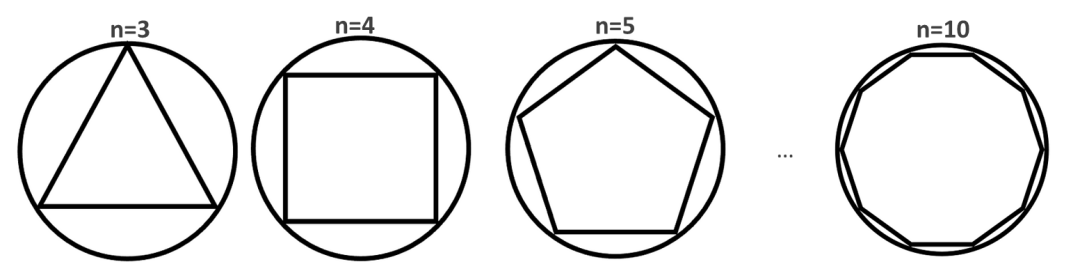
随着n变得越来越大,多边形变得越来越像圆形。如果正多边形边数n非常大,我们可以将正多边形的周长近似等于圆的周长,也就可以近似求出π。具体的推理过程忽略,直接参考下面代码:
import mathdef approximate_pi(n, d=2): r = d/2 a = 360/n x = (2 * r**2 * (1 - math.cos(math.radians(a))))**0.5 perimeter = x * n pi = perimeter / d return pifor n in [3,4,5,10,100,1000,10000,100000]: print(n, "-->", approximate_pi(n))
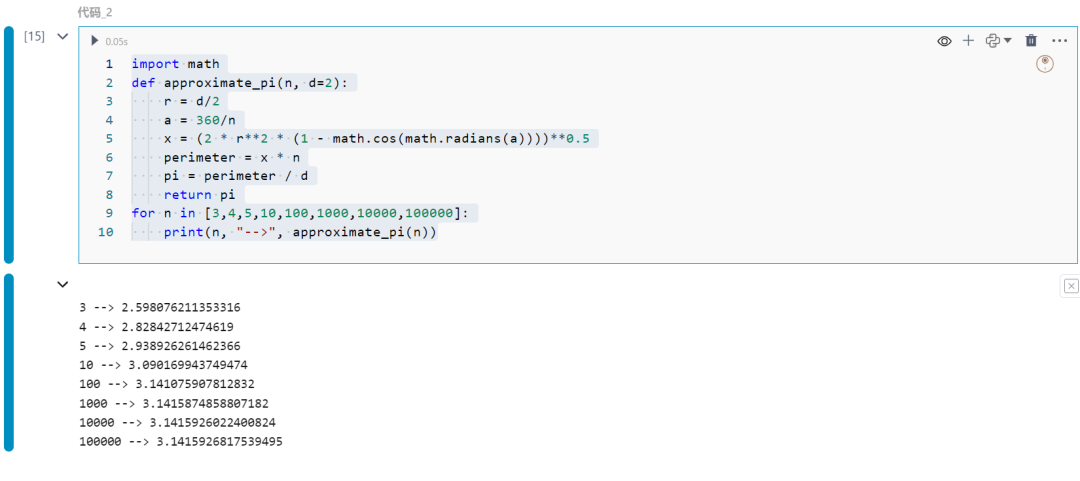
随着N 逐步变大,π约精确。
蒙特卡罗方法(The Monte Carlo Method)
蒙特卡罗方法是一种基于概率的算法,通过随机采样的方式来估计π的值。这种方法模拟了在一个单位正方形内随机撒点,然后统计落在单位圆内的点的比例,通过这个比例来估计π的值。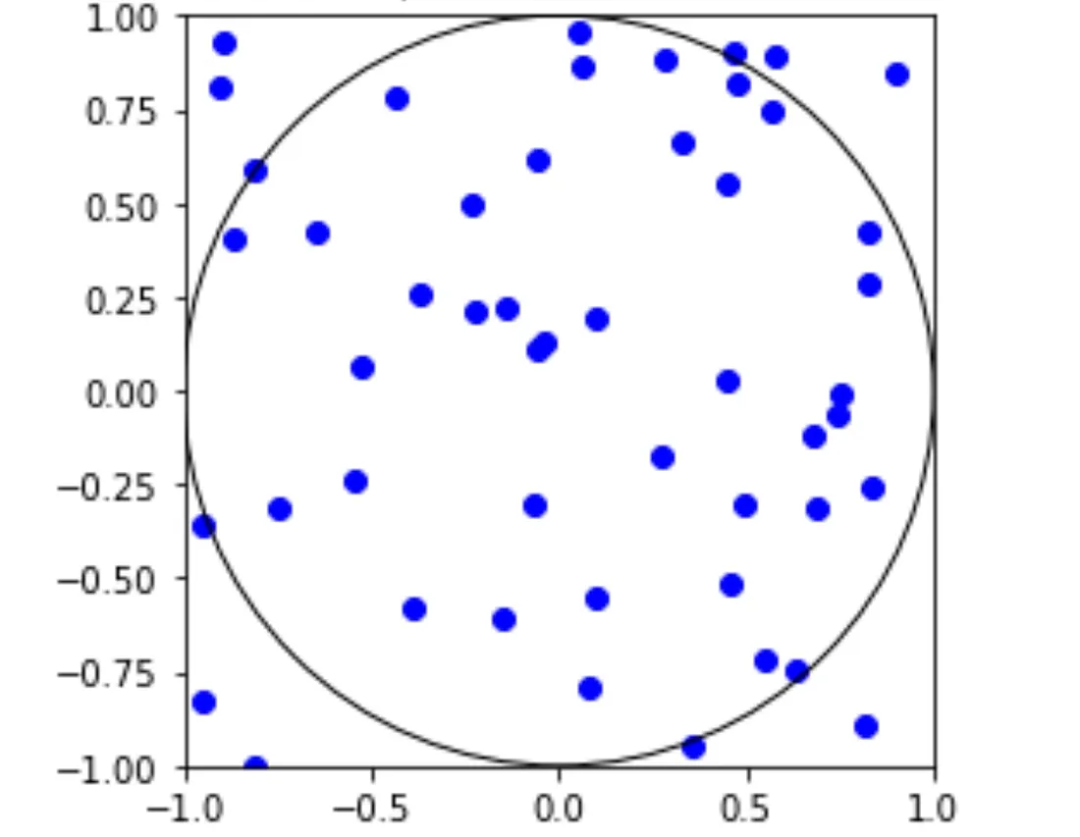
如上图假设一个半径为1.0、以原点 (0,0) 为中心的圆,以及一个从 -1.0 到 1.0 的正方形。通过随机在正方形内设置点,我们可以计算圆内的点数与总点数的比例,进而近似推导出圆的面积与正方形的面积之间的关系。随着随机坐标点的数量增加,圆内的点数与总点数的比例将逐渐趋近于 π 值。因此,我们可以利用这种统计的方法,通过计算圆内点数与总点数的比例乘以4来近似π的值。
import random
def pi_estimate(N): inside_quadrant = 0 for i in range(0, N): x_i = random.random() * 2 - 1 y_i = random.random() * 2 - 1 if (x_i ** 2 + y_i ** 2) <= 1: inside_quadrant += 1 return (inside_quadrant / N) * 4
for n in [10, 100, 1_000, 10_000, 100_000, 1_000_000, 10_000_000]: print(f"n={n} ", pi_estimate(n))

应用列表推导式,简化为一行代码:
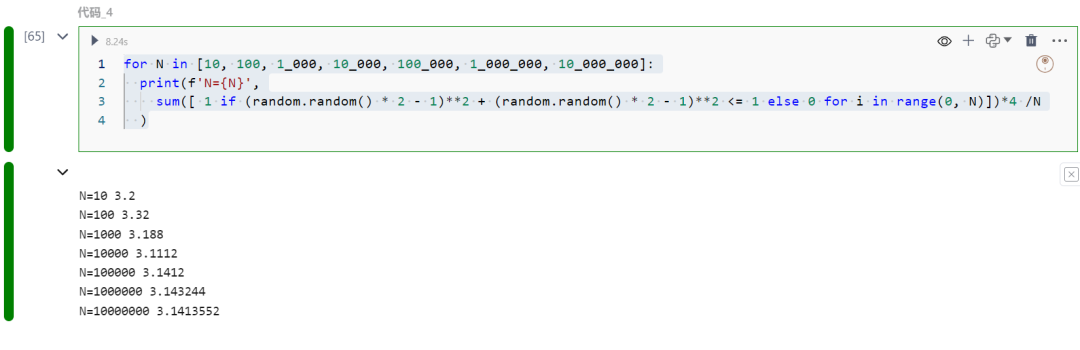
for N in [10, 100, 1_000, 10_000, 100_000, 1_000_000, 10_000_000]: print(f'N={N}', sum([ 1 if (random.random() * 2 - 1
)**2 + (random.random() * 2 - 1)**2 <= 1 else 0 for i in range(0, N)])*4 /N )
无穷级数方式(例如:π的莱布尼茨公式)
π莱布尼兹公式,它是一种基于级数展开的方法。通过使用无穷级数,可以逐步逼近π的值。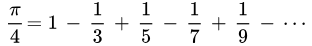
使用求和符号可记作(证明略):
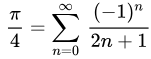
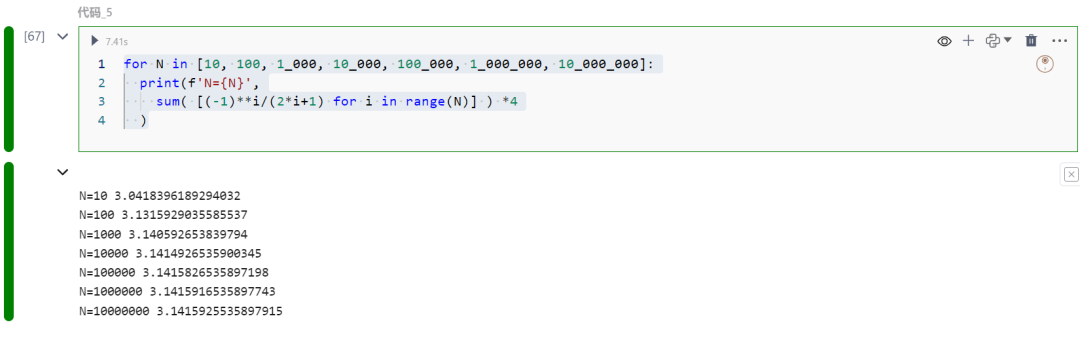
for N in [10, 100, 1_000, 10_000, 100_000, 1_000_000, 10_000_000]: print(f'N={N}', sum( [(-1)**i/(2*i+1) for i in range(N)] ) *4 )
Chudnovsky 算法(楚德诺夫斯基算法)
Chudnovsky算法是一种高效的算法,能够快速计算π的值。这种算法基于超越函数的性质和复杂的数学理论,通过迭代和逼近的方式,可以快速而准确地计算π的值。1988年,两兄弟大卫和格雷戈里·丘德诺夫斯基(David and Gregory Chudnovsky)发表了一种引人注目的算法,彻底改变了π的计算方法。Chudnovsky算法是一种快速而优雅的方法,可以在每一次求和步骤中生成14位或更多位的π,这是基于印度数学天才斯里尼瓦萨·拉马努金(Srinivasa Ramanujan)的一些公式。
详情参考:https://en.wikipedia.org/wiki/Chudnovsky_algorithm
Chudnovsky算法已被用于实现多项π的世界纪录计算,例如2009年的2.7万亿位、2011年的10万亿位、2016年的22.4万亿位、2019年的31.4万亿位、2020年的50万亿位、2021年的62.8万亿位以及2022年的100万亿位。
Chudnovsky算法python 实现参考:https://github.com/wblazej/pi-chudnovsky/blob/master/src/pi.py
代码如下:
import math
class PI: digits: int
def __init__(self, digits: int): self.digits = digits self.c = 640320 self.c3_over_24 = self.c ** 3 self.one = 10 ** digits
def calc(self): n = int(self.digits / math.log10(self.c3_over_24 / 6 / 2 / 6) + 1) _, q, t = self.bs(0, n) sqrt_c = self.sqrt(10005 * self.one) return (q * 426880 * sqrt_c)
def bs(self, a, b): if b - a == 1: if a == 0: pab = qab = 1 else: pab = (6 * a - 5) * (2 * a - 1) * (6 * a - 1) qab = a ** 3 * self.c3_over_24
tab = pab * (13591409 + 545140134 * a)
if a & 1: tab = -tab else: m = (a + b) pam, qam, tam = self.bs(a, m) pmb, qmb, tmb = self.bs(m, b) pab = pam * pmb qab = qam * qmb tab = qmb * tam + pam * tmb return pab, qab, tab
def sqrt(self, n): floating_point_precision = 10 ** 16 n_float = float((n * floating_point_precision) x = (int(floating_point_precision * math.sqrt(n_float)) * self.one) n_one = n * self.one
while True: x_old = x x = (x + n_one
if x == x_old: break
return x
pi=PI(10000).calc()pi
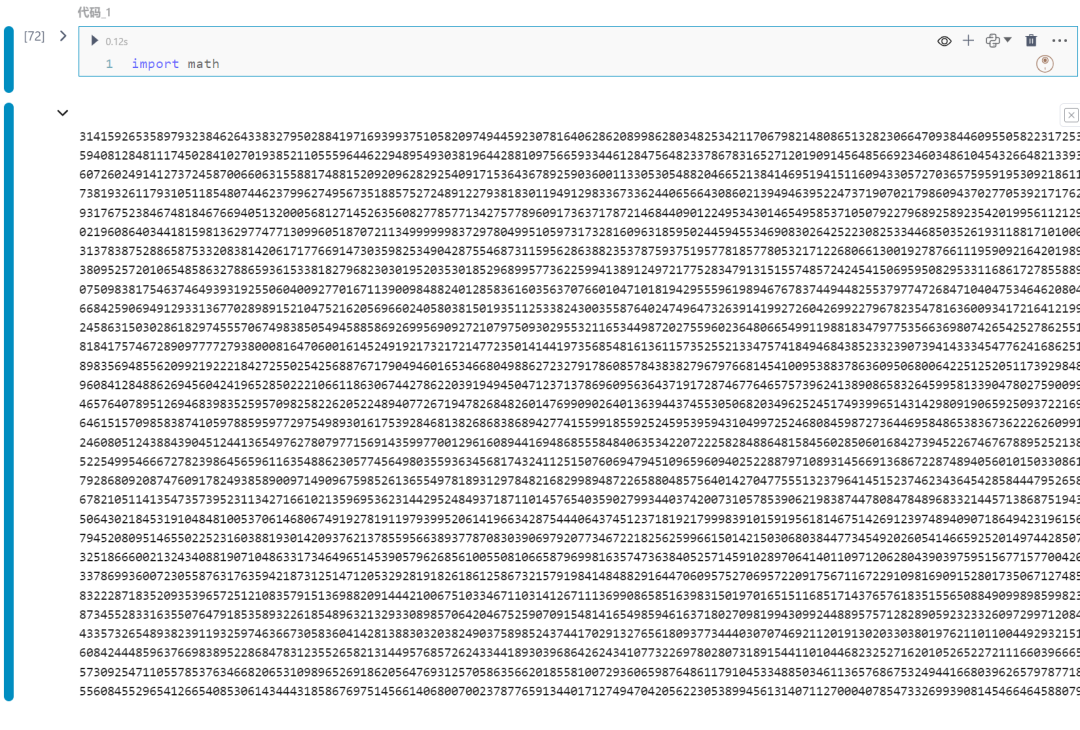
以上代码输出1万位的π,经过和http://www.geom.uiuc.edu/~huberty/math5337/groupe/digits.html 比对是一致的。
庆祝圆周率日的日子里,我们通过四种不同的方法展示了计算π的方式:逼近法、蒙特卡罗方法、莱布尼茨公式和Chudnovsky算法。每种方法都有其独特的原理和逼近π的方式,从直观到数学化,从概率到级数展开,以及更高效的Chudnovsky算法。这些方法的探索不仅是对数学的致敬,也是对Python编程的致敬,展现了数学之美与编程的魅力。