今天为大家带来的是2023年12月认证Python八级真题解析回顾。
CCF编程能力等级认证,英文名Grade Examination of Software Programming(以下简称GESP),由中国计算机学会发起并主办,是为青少年计算机和编程学习者提供学业能力验证的平台。GESP覆盖中小学全学段,符合条件的青少年均可参加认证。GESP旨在提升青少年计算机和编程教育水平,推广和普及青少年计算机和编程教育。
GESP考察语言为图形化(Scratch)编程、Python编程及C++编程,主要考察学生掌握相关编程知识和操作能力,熟悉编程各项基础知识和理论框架,通过设定不同等级的考试目标,让学生具备编程从简单的程序到复杂程序设计的编程能力,为后期专业化编程学习打下良好基础。
本次为大家带来的是2023年12月份Python 八级认证真题解析。
一、单选题(每题2分,共30分)

1、小杨要从A城到B城,又想顺路游览一番。他有两个选项:1、坐高铁路到C城游览,再坐高铁或飞机到B城;2、坐船到D城游览,再坐船、高铁或飞机到B城。请问小杨从A城到B城共有几种交通方案可以选择?( )。
A. 2
B. 3
C. 5
D. 6
【答案】C
【解析】本题本质是一道数学题目,将问题分为2部分,第一部分为A->C->B,有2种方案,第二部分为A->D->B,有3种方案,加起来是5种,选择C。
2、在 Python 定义 fuc1()函数如下。有关调用该函数的说法,正确的是( )。
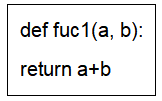
A. 调用 func1()函数时,如果参数 a 为类似二维数组 list,b 为一维 list,函数调用不会报错;
B. 调用 func1()函数时,如果参数 a 为类似二维数组 list,b 为一维 list,函数调用将会报错;
C. 调用 func1()函数时,如果参数 a 和 b 的类型均为 tuple,b 也为 tuple,函数调用将会报错;
D. 调用 func1()函数时,如果参数 a 和 b 的类型为 dict,函数调用将会报错;
【答案】A
【解析】本题考察的是“+”号的运算,其中A,B选择是关于列表的加法,是将两个列表的拼接成一个列表,不会报错。C选项是关于元组的加法,元组是不可修改的,但是两个元组相加是生成了另一个元组,并不会修改原始元组,不会报错。D选项是关于字典的加法,字典相加也是将两个字典合并成一个新的字典,不会报错。选择A。
3、下面有关 Python 类和对象的说法,错误的是( )。
A. 对象的生命周期开始时,会执行构造函数。
B. 对象的生命周期结束时,会执行析构函数。
C. 类的析构函数可以为虚函数。
D. 类的构造函数可以为虚函数。
【答案】D
【解析】本题中,对象的生命周期开始和结束分别会执行构造函数和析构函数,所以A,B,正确。对于虚函数,在python中是虚函数的装饰器有@abstractmethod和@virtual,并且是通过继承和方法重写来实现的,其中构造函数不能当成虚函数使用,因为创建一个对象时我们总是要明确指定对象的类型,尽管我们可能通过基类的指针或引用去访问它但析构却不一定,我们往往通过基类的指针来销毁对象。这时候如果析构函数不是虚函数,就不能正确识别对象类型从而不能正确调用析构函数。选择D。
4、使用邻接矩阵表达 n 个顶点的有向图,则该矩阵的大小为( )。
A. n×(n+1)
B. n×n
C. n×(n−1)
D. 2n×(n−1)/2
【答案】B
【解析】邻接矩阵的行列分别为n个,大小则为n*n。选择B。
5、5 位同学排队,其中⼀位同学不能排在第⼀,则共有多少种可能的排队⽅式?( )。
A. 5
B. 24
C. 96
D. 120
【答案】C
【解析】本题是排序题目,5位同学排序方法有A55,减去指定同学排在第一位的情况A44,则有120-24=96,选择C。
6、⼀个⽆向图包含 n 个顶点 ,则其最⼩⽣成树包含多少条边?( )。
A. n - 1
B. n
C. n + 1
D. 最⼩⽣成树可能不存在。
【答案】D
【解析】n个顶点的组成的树有n-1条边,但是没有保证为连通图,所以不能判断是否存在最小生成树,选择D。
7、已知三个 double 类型的变量a、b和theta分别表⽰⼀个三角形的两条边长及⼆者的夹角(弧度),则下列哪个表达式可以计算这个三角形的⾯积?( )。
A. a * b * s in(theta) / 2
B. (a + b) * s in(theta) / 20
C. a * b * cos(theta) / 2
D. sqrt(a * a + b * b - 2 * a * b * cos(theta))
【答案】A
【解析】本题是数学题目,三角形的面积是(底*高)/2,其中,如果以b为底,还缺少高,通过三角函数,h=a*sin(theta),带入公式,a*b* sin(theta)/2,选择A。
8、对有 n 个元素的⼆叉排序树进⾏中序遍历,其时间复杂度是( )。
A. O(1)
B. O(log(n))
C. O(n)
D. O(n2)
【答案】C
【解析】树的遍历是将每个元素遍历一次,因此时间复杂度为O(n),选择C。
9、假设输⼊参数m和n满⾜m≤n,则下⾯程序的最差情况的时间复杂度为( )。

A. O(log(n))
B. O(n)
C. O(n × m)
D. O(m × log(n)
【答案】A
【解析】本题是辗转相除法求最大公倍数,所以时间复杂度为O(log(n)),选择A。
10、下⾯程序的时间复杂度为( )。
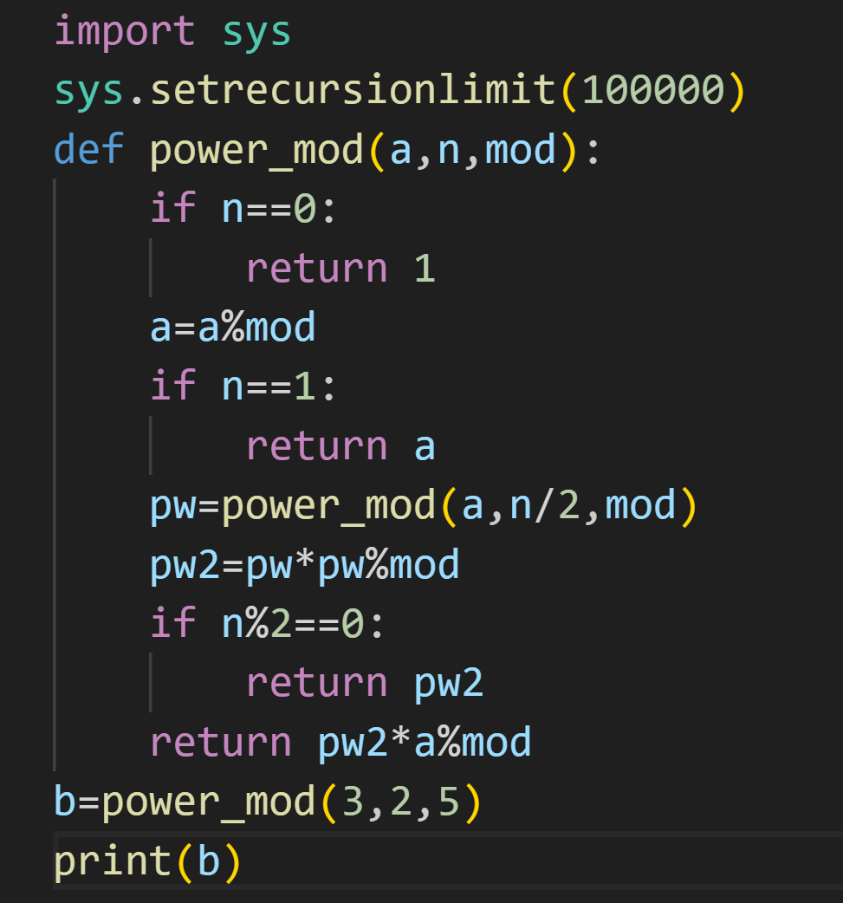
A. O(n)
B. O(an)
C. O(log(n))
D. O(log(n) × a)
【答案】C
【解析】本题是关于快速幂的程序,是计算a**n%mod,每次n的值都会/2,所以时间复杂度为O(logn),选择C。
11、下⾯程序的时间复杂度为( )。

A. O(2n)
B. O(2m × (n - m))
C. O(c(n, m))
D. O(m × (n - m))
【答案】D
【解析】本题是使用了递归算法,并且对求出的值进行了记录,简化了算法的时间复杂度,通过打表的方法,记录对应的值,可以发现总共访问了m*(n-m)个元素,选择D。
12、下⾯的程序使⽤出边的邻接表表达有向图,则下列选项中哪个是它表达的图?( )。
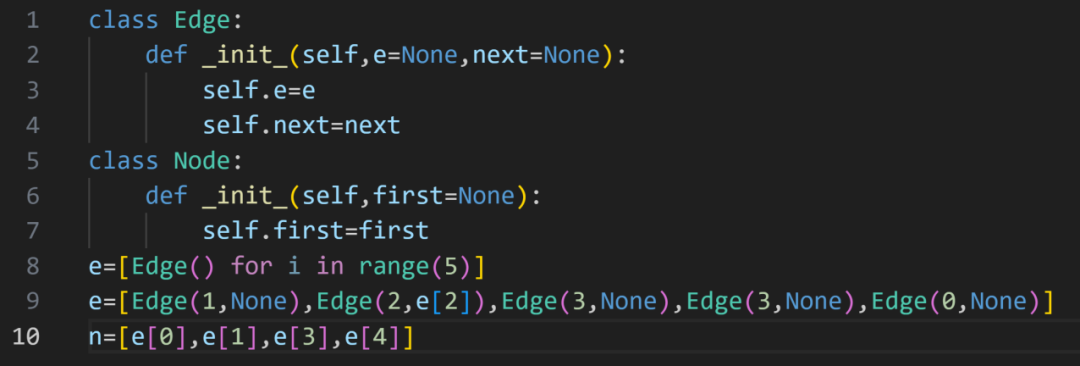
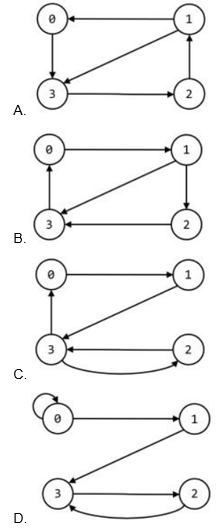
【解析】结构体edge里的next指向的是下一条边,Node里的first指向的是每个点的第一条边,所以0号点指向1号点,1号点指向2,3号点,2号点指向3号点,3号点指向0号点,
概念图是
最接近的符合代码描述的选项是B。
13、下⾯程序的输出为( )。

A. 12
B. 18
C. 36
D. 42
【答案】B
【解析】本题是三重for循环,a,b,h取值范围都为(1,10],当满足条件(a+b)*h==20时,计数器+1。因为(a+b)*h==20,所以h的值有1,2,4,5,10,那对应的a+b的值有20,10,5,4,2 方案数分别为1,9,4,3,1,总共18种,选择B。
14、下⾯程序的输出为( )。
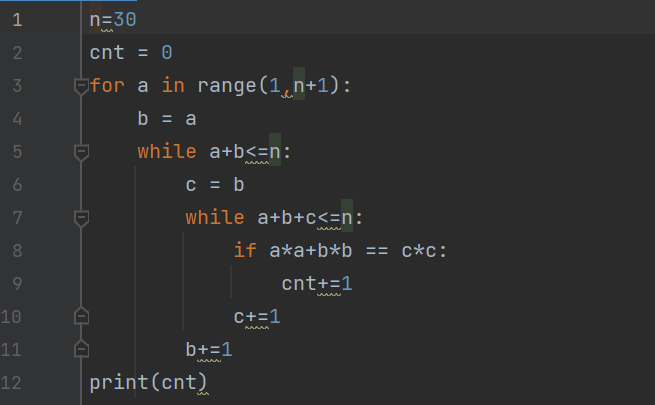
A. 3
B. 6
C. 11
D. 22
【答案】A
【解析】本题代码中要求a,b,c都是正整数,满足a+b+c<=30且a^2+b^2=c^2,符合要求的a,b,c有3 4 5;5 12 13;6 8 10共3种,选A。
15、下⾯的程序中 ,⼆维数组 h 和 v 分别代表如下图所⽰的⽹格中的⽔平边的时间消耗和垂直边的时间消耗。程序使⽤动态规划计算从左下角到右上角的最⼩时间消耗 ,则横线处应该填写下列哪个选项的代码?( )。


A.dis[i][j] = min(dis[i - 1][j] + v[i - 1][j], dis[i][j - 1] + h[i][j - 1]);
B.dis[i][j] = min(dis[i - 1][j] + h[i - 1][j], dis[i][j - 1] + v[i][j - 1]);
C.dis[i + 1][j + 1] = min(dis[i][j + 1] + v[i][j + 1], dis[i + 1][j] + h[i + 1][j]);
D.dis[i + 1][j + 1] = min(dis[i][j + 1] + h[i][j + 1], dis[i + 1][j] + v[i + 1][j]);
【答案】C
【解析】本题要求计算从网格的左下角到右上角的最小时间消耗。二维数组v和h分别表示网格中的水平边和垂直边的时间消耗。程序使用动态规划方法计算这个最小时间。
动态规划状态转移方程需要根据网格的边长和时间消耗来设置。在第11行的输出dis[y][x],我们注意到枚举的范围是
二、判断题(每题2分,共20分)

1、python语言非常强大,可以用来求解方程的解。例如,如果变量x为float类型的变量,则执行语句x * 2 - 4 = 0;后,变量x的值会变为2.0。
【答案】错误
【解析】本题中x*2-4=0既不是赋值语句,也不是判断语句,所以不能通过编译。错误。
2、⼀个袋⼦中有3个完全相同的红⾊⼩球、2个完全相同的蓝⾊⼩球 。每次从中取出1个 ,且不放回袋⼦ ,这样 进⾏3次后 ,将取出的⼩球依次排列 ,则可能的颜⾊顺序有7种。
【答案】正确
【解析】将所有情况进行枚举,分别为:红红红,红红蓝,红蓝红,蓝红红,红蓝蓝,蓝红蓝,蓝蓝红。正确。
3、杨辉三角 ,是⼆项式系数的⼀种三角形排列 ,在中国南宋数学家杨辉1261年所著的《详解九章算法》⼀书中 出现 ,是中国数学史上的⼀项伟⼤成就。
【答案】正确
【解析】本题是历史题,杨辉三角,是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉所著的《详解九章算法》中出现。正确。
4、N个顶点的有向完全图(不带⾃环)有N × (N-1)/2条边。
【答案】错误
【解析】有向完全图,(x,y)和(y,x)不算同一条边,所以有n*(n-1)条边。错误。
5、如果待查找的元素确定 ,只要哈希表的⼤⼩不⼩于查找元素的个数 ,就⼀定存在不会产⽣冲突的哈希函数。
【答案】正确
【解析】在极端情况下,可以先将待查找元素放进哈希表中,再根据位置构造一个由if-else判断组成的哈希函数:当查找元素与某一项待查找相同时,返回对应的位置。虽然这样构造的哈希函数的时间复杂度较高,但满足不会产生冲突。正确。
6、动态规划算法的时间复杂度⼀般为:必要状态的数量 ,乘以计算⼀次状态转移⽅程的时间复杂度。
【答案】正确
【解析】动态规划的时间复杂度⼀般为状态数*转移复杂度。正确。
7、已知 int 类型的变量 a 、 b 和 h 中分别存储着⼀个梯形的顶边长、底边长和⾼ ,则这个梯形的⾯积可以通 过表达式 (a + b) * h / 2 求得。
【答案】错误
【解析】本题考察梯形的面积公式,正确。
8、判断图是否连通只能⽤⼴度优先搜索算法实现。
【答案】错误
【解析】还可以使用深度优先算法。错误。
9、在N个元素的⼆叉排序树中查找⼀个元素 ,最好情况的时间复杂度是0(logN)。
【答案】错误
【解析】最好的情况下是O(1),一次就可以找到。错误。
10、给定float类型的变量x,且其值大于等于0,我们可以通过二分法求出根号x即x1/2
【答案】正确
【解析】二分法要求查找的元素是有序排列的,f(x)=x1/2在x∈[0,+∞)上是单调递增。正确。
三、编程题(每题25分,共50分)

1、奖品分配
问题描述
班上有N名同学 ,学号从0到N-1。有M种奖品要分给这些同学,其中,第i种奖品总共有ai个 (i = 0,1,...,M -1)。巧合的是,奖品的数量不多不少,每位同学都可以恰好分到⼀个奖品,且最后剩余的奖品不超过1个(即:N ≤
a0 +a1+....+aM-1 ≤ N+1))。
现在,请你求出每个班级礼物分配的⽅案数,所谓⽅案,指的是为每位同学都分配⼀个种类的奖品。只要有⼀位同学获得了不同种类的奖品,即视为不同的⽅案。⽅便起见,你只需要输出⽅案数对109+7取模后的结果即可。
共有T个班级都⾯临着奖品分配的问题,你需要依次为他们解答。
输入描述
第一行一个整数 T,表示班级数量。
接下来工行,每行若千用单个空格隔开的正整数。首先是两个正整数 N,M,接着是 M 个正整数a0 ,a1,....,aM-1 ,保证N ≤ a0 +a1+....+aM-1 ≤ N+1。
输出描述
输出T行,每行一个整数,表示该班级分配奖品的方案数对 109+ 7取模的结果。
特别提醒
在常规程序中,输入、输出时提供提示是好习惯。但在本场考试中,由于系统限定,请不要在输入、输出中附带任何提示信息。
样例输入1

样例输出1

样例解释1
对于第1个班级,学号为0,1,2的同学可以依次分别获得奖品 0,1,1,也可以依次分别获得奖品1,0,1,也可以依次分别获得奖品1,1,0,因此共有3种方案。
对于第2个班级,学号为0,1,2 的同学可以依次分别获得奖品0,1,1,也可以依次分别获得奖品 1,0,1,也可以依次分别获得奖品1,1,0,可以依次分别获得奖品1,1,1,因此共有4种方案。
对于第3个班级,可以把编号为1的奖品分配给5名同学中的任意一名,共有5种方案;再把编号为2的奖品分配给剩余4名同学中的任意一名,共有4种方案;最后给剩余3名同学自然获得0号奖品。因此,方案数为5x4=20。
样例输入2

样例输出2

数据规模
对于30%的测试点,保证 N≤10。
对于另外30%的测试点,保证 M =2。
对于所有测试点,保证 N ≤ 1,000; 保证T ≤ 1,000;保证 M ≤ 1,001。
【解题思路】根据样例1中是数据,3 2 1 2,人数n=3,种类m=2,商品总数为1+2=3个,商品数和人数相同,所以可以使用组合数来统计有多少种方案,C(3,1)*C(2,2)=3。
3 2 1 3,人数n=3,种类m=2,商品总数1+3=4个,此时商品数大于人数,我们可以不必要考虑人数,只考虑商品数,所以使用组合数得到:C(4,1)*C(3,3)=4个。
因此我们发现用组合数来处理排列方式,可以使用杨辉三角预处理下所有情况的组合数,放到列表C中,然后再根据实际情况n和m的组合,寻找到相应的值。
【参考程序】
def main():
P = 10**9 + 7
max_n = 1001
C = [[0 for _ in range(max_n + 1)] for __ in range(max_n + 1)]
for i in range(max_n + 1):
for j in range(i + 1):
if j == 0 or j == i:
C[i][j] = 1
else:
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % P
T = int(input())
for t in range(T):
inp = list(map(int, input().strip().split(' ')))
n = inp[0]
a = inp[2:]
if n + 1 == sum(a):
n += 1
ans = 1
for m in a:
ans = ans * C[n][m] % P
n -= m
assert n == 0
print(ans)
if __name__ == "__main__":
main()
2、大量的工作沟通
问题描述
某公司有N名员工,编号从0至 N-1。其中,除了0 号员是老板,其余每名员工都有一个直接领导。我们假设编号为i的员工的直接领导是 fi。
该公司有严格的管理制度,每位员工只能受到本人或直接领导或间接领导的管理。具体来说,规定员工x可以管理员工y,当且仅当x=y,或x=fy或x可以管理fy。特别,0号员工老板只能自我管理,无法由其他任何员管理。
现在,有一些同事要开展合作,他们希望找到一位同事来主持这场合作,这位同事必须能够管理参与合作的所有同事。如果有多名满足这一条件的员工,他们希望找到编号最大的员工。你能帮帮他们吗?
输入描述
第一行一个整数 N,表示员工的数量。
第二行 N-1个用空格隔开的正整数,依次为 f1,f2,...,fn-1。
第三行一个整数 Q,表示共有 Q 场合作需要安排。
接下来Q行,每行描述一场合作: 开头是一个整数 m(2≤ m≤ N),表示参与本次合作的员工数量;接着是m个整数,依次表示参与本次合作的员工编号 (保证编号合法且不重复)。
保证公司结构合法,即不存在任意一名员工,其本人是自己的直接或间接领导。
输出描述
输出Q行,每行一个整数,依次为每场合作的主持人选。
特别提醒
在常规程序中,输入、输出时提供提示是好习惯。但在本场考试中,由于系统限定,请不要在输入、输出中附带任何提示信息。
样例输入1

样例输出1

样例解释1
对于第一场合作,员工3,4有共同领导2,可以主持合作。
对于第二场合作,员工2本人即可以管理所有参与者。
对于第三场合作,只有0号老板才能管理所有员工。
样例输入2

样例输出2

数据规模
对于25%的测试点,保证 N ≤ 50。
对于50%的测试点,保证 N ≤ 300。
对于所有测试点,保证3≤ N ≤ 105;保证Q ≤ 100,保证 m≤ 104
【解题思路】分析样例可得本题是求最近的共同祖先问题。从样例1中可得3,4的最近共同祖先是2;2,3,4的共同祖先是2;1,4的共同祖先是0。我们可以先把所有元素的祖先进行预处理,放到列表中,然后每个元素的深度也存储到列表中,通过BFS搜索算法来求出元素的共同祖先,并记录在列表中。
【参考程序】
def main():
n = int(input())
father = [-1] + list(map(int, input().split(' ')))
child = [[] for i in range(n)]
for i in range(1, n):
child[father[i]].append(i)
depth = [0 for i in range(n)]
anc = [[] for i in range(n)]
max_anc_id = [i for i in range(n)]
queue = [0]
# BFS
while queue:
node = queue[0]
queue = queue[1:]
anc[node].append(father[node])
for i in range(1, 20):
if anc[node][i - 1] == -1:
anc[node].append(-1)
else:
anc[node].append(anc[anc[node][i - 1]][i - 1])
for c in child[node]:
depth[c] = depth[node] + 1
max_anc_id[c] = max(c, max_anc_id[node])
queue.append(c)
def lca(u, v):
if depth[u] > depth[v]:
u, v = v, u
for i in range(20):
if (depth[v] - depth[u]) & (1 << i):
v = anc[v][i]
assert depth[u] == depth[v]
if u == v:
return u
for i in range(len(anc[u]) - 1, -1, -1):
if anc[u][i] != anc[v][i]:
u = anc[u][i]
v = anc[v][i]
if father[u] != father[v]:
_u, _v = u, v
while u != -1 and v != -1:
u = father[u]
v = father[v]
u, v = _u, _v
assert father[u] == father[v]
return father[u]
q = int(input())
for _ in range(q):
x = list(map(int, input().split(' ')))[1:]
ans = x[0]
for u in x[1:]:
ans = lca(ans, u)
print(max_anc_id[ans])
if __name__ == "__main__":
main()