组合优化问题是一类在计算机科学和运筹学中常见的问题,比如旅行商问题、背包问题、图着色问题等。这类问题通常涉及在给定数量的候选解中找到最优解。传统的解决方法通常采用穷举法或者近似算法,但组合优化问题解的数量往往是随问题的规模呈指数增长,当问题规模增大时,以上方法就显得很低效。
机器学习技术为解决这类问题提供了一种新的方法,利用机器学习求解组合优化问题也是人工智能的前沿方向,在今年的各大顶会收录论文中,相关的科研成果数目也十分可观。
我这次就帮同学们整理了20篇机器学习组合优化方向的顶会论文,都是今年最新,包含图匹配、旅行商问题、二次分类问题、因果发现等多个细分方向。
扫码添加小享,回复“组合优化”
免费获取全部论文及代码合集

1.Revocable Deep Reinforcement Learning with Affinity Regularization for Outlier-Robust Graph Matching. ICLR, 2023
具有亲和正则化的可撤销深度强化学习
「简述:」论文提出了一种基于深度强化学习的图匹配方法RGM。该方法采用顺序节点匹配方案,自然适用于选择性内匹配策略来对抗离群点。此外,作者还设计了一个可撤销动作框架,以提高代理在复杂约束图匹配中的灵活性,还提出了一种二次近似技术来正则化亲和度得分,以在存在离群点的情况下进行。因此,当亲和度得分停止增长时,代理可以及时完成内匹配,否则需要额外的参数(即内点的数量)来避免匹配离群点。
2.Towards Quantum Machine Learning for Constrained Combinatorial Optimization: a Quantum QAP Solver. ICML, 2023
量子机器学习在约束组合优化中的应用
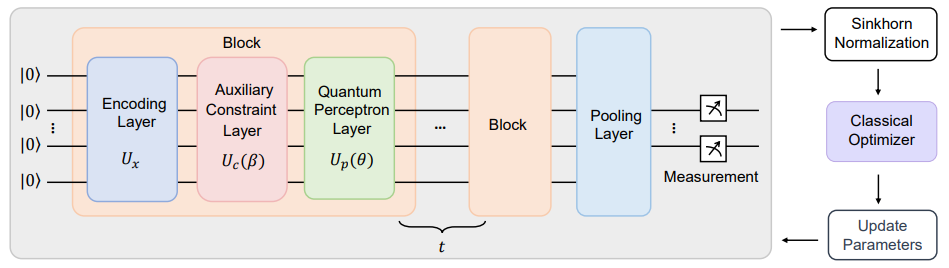
「简述:」论文提出了一个用于解决组合优化问题的新型量子神经网络(QNN)。这个神经网络被命名为QAP-QNN,它能将二次分配问题(QAP)转化为约束顶点分类任务。QAP-QNN将匹配约束和节点排列不变性考虑在内。此外,文章还在TorchQauntum模拟器上研究了图匹配和旅行商问题这两个QAP任务,实验结果表明该方法的有效性。
3.LinSATNet: The Positive Linear Satisfiability Neural Networks. ICML, 2023.
正线性可满足性神经网络
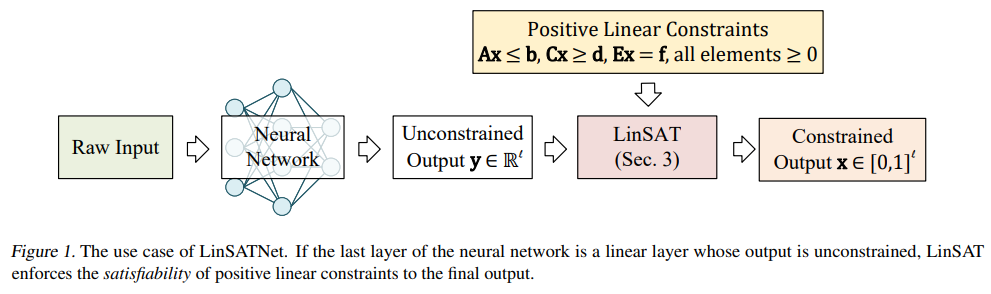
「简述:」本文介绍了一种将线性可满足性引入神经网络的方法,并提出了第一个基于经典Sinkhorn算法扩展的可微分可满足性层。作者展示了这种技术在解决约束问题方面的有效性,包括神经路由、部分图匹配和金融投资组合预测等场景。据作者所知,目前还没有一次性神经网络求解器可以解决这些情况。
4.Optimizing Solution-Samplers for Combinatorial Problems: The Landscape of Policy-Gradient Methods. NeurIPS, 2023.
优化组合问题的解决方案采样器
「简述:」本文介绍了一种新理论框架,用于分析深度神经网络和强化学习方法在解决组合问题方面的有效性。作者提出了一些问题,比如是否存在具有足够表达能力、可处理性和良性优化景观的生成模型。通过对这些问题的研究,作者得出了肯定的答案,并证明了该方法适用于多种组合问题。同时,作者还引入了一种新颖的正则化过程,有助于解决梯度消失和避免不良的静止点。

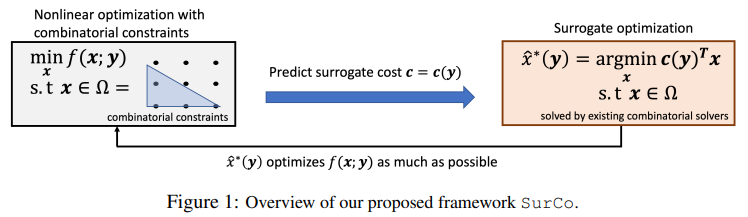
5.SurCo: Learning Linear Surrogates For Combinatorial Nonlinear Optimization Problems. ICML, 2023.
学习组合非线性优化问题的线性替代方案
「简述:」论文介绍了一种名为SurCo的方法,用于解决具有非线性成本函数和组合约束条件的实际优化问题。作者提出了学习线性替代成本的SurCo,它可以用于现有的组合求解器中,以输出原始非线性组合优化问题的好解决方案。作者还提出了三种SurCo变体,并通过实验表明,在现实世界的优化问题中,SurCo比最先进的方法和领域专家方法更快地找到了更好的解决方案。
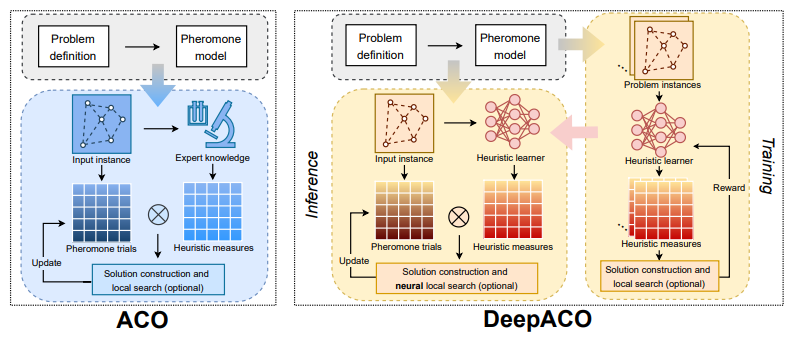
6.DeepACO: Neural-enhanced Ant Systems for Combinatorial Optimization. NeurIPS, 2023.
用于组合优化的神经增强蚂蚁系统
「简述:」论文提出了一种名为DeepACO的通用框架,利用深度强化学习自动进行知识驱动的启发式设计。DeepACO旨在加强现有ACO算法的启发式措施,并在未来ACO应用中省去繁琐的手动设计。作为一种神经增强的元启发式方法,DeepACO使用单个神经模型和一组超参数在八个组合优化问题上始终优于ACO同类算法。作为神经组合优化方法,DeepACO在典型路由问题上的表现与特定问题方法相当或更好。
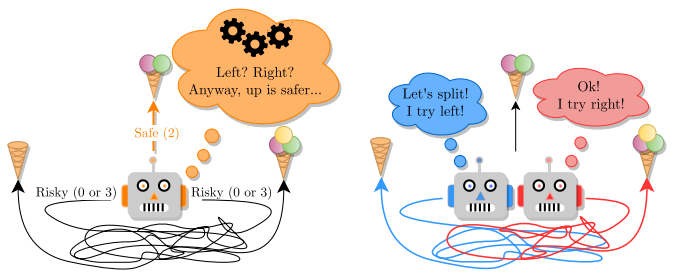
7.Winner Takes It All: Training Performant RL Populations for Combinatorial Optimization. NeurIPS, 2023.
训练用于组合优化的高性能RL群体
「简述:」本文介绍了一种使用强化学习解决组合优化问题的方法,并提出了训练一组互补策略的建议。作者认为,同时使用多个策略可以提高解决问题的效率。作者引入了Poppy,一种简单的训练程序,用于生成一组互补策略。实验结果表明,这种方法在四个流行的NP-hard问题上获得了很好的结果。
8.ROCO: A General Framework for Evaluating Robustness of Combinatorial Optimization Solvers on Graphs. ICLR, 2023
一种用于评估图上组合优化求解器鲁棒性的通用框架
「简述:」论文提出了一种评估组合优化求解器鲁棒性的通用框架。无论求解器是经典的,还是基于学习的,都可以用这个框架来评估其鲁棒性。作者还开发了一个实用的鲁棒性度量,解决了输入实例扰动的不可微分挑战,并通过实验展示了最先进求解器在硬实例上的性能下降。这引发了对组合优化求解器鲁棒性的关注。

9.Towards Omni-generalizable Neural Methods for Vehicle Routing Problems. ICML, 2023.
面向车辆路线问题的泛化神经方法
「简述:」本文研究了面向车辆路径问题的学习方法,并提出了一种新的元学习方法。现有的方法通常在固定大小和节点分布的任务上进行训练和测试,因此其泛化性能有限。作者考虑了VRP中大小和分布两个方面的泛化问题,并提出了一种通用的元学习框架,该框架能够有效地训练一个初始化模型,使其能够在推理过程中快速适应新任务。此外,作者还开发了一种简单而高效的近似方法来减少训练开销。
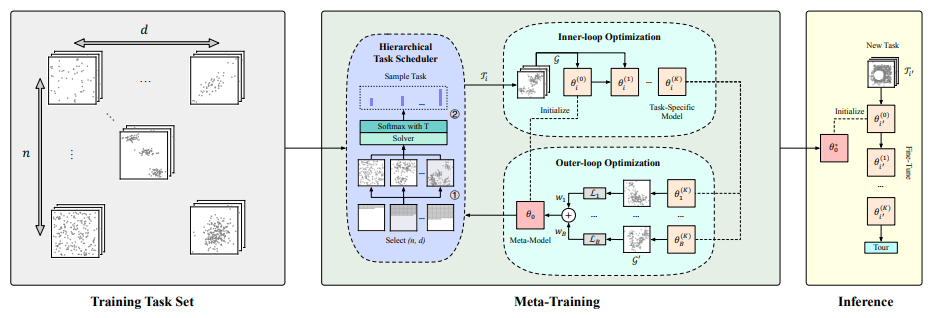
10.Meta-SAGE: Scale Meta-Learning Scheduled Adaptation with Guided Exploration for Mitigating Scale Shift on Combinatorial Optimization. ICML, 2023.
用于缓解组合优化中规模变化的规模元学习调度自适应方法
「简述:」论文提出了一种名为Meta-SAGE的新方法,用于提高深度强化学习模型在组合优化任务上的可扩展性。该方法通过使用规模元学习器和调度自适应来适应测试时更大尺度的问题。作者引入了局部性偏差,以鼓励选择附近的位置来确定下一个位置。实验结果表明,Meta-SAGE优于先前的自适应方法,并在代表性CO中显著提高了可扩展性。
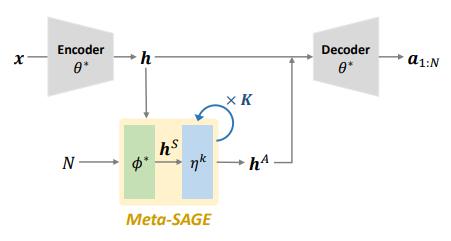
11.Efficient Meta Neural Heuristic for Multi-Objective Combinatorial Optimization. NeurIPS, 2023.
多目标组合优化的高效元神经启发式算法
「简述:」论文提出了一种高效的元神经启发式算法(EMNH),用于解决多目标组合优化问题。该算法通过并行学习提高训练效率,并使用对称采样方法稳定训练。在微调过程中,该算法采用高效分层方法,以系统地解决所有子问题。实验结果表明,EMNH在解决方案质量和学习效率方面优于现有的神经启发式算法,同时消耗的时间更短。
12.Improved Algorithms for Multi-period Multi-class Packing Problemswith Bandit Feedback. ICML, 2023.
多周期多物品装箱问题的改进算法
「简述:」论文讨论了一个复杂的优化问题,即线性上下文多类多期装箱问题(LMMP)。这个问题要求在给定预算下,尽可能地优化物品的打包方式,以最大化总价值。作者提出了一种新的估计方法,可以更快地收敛,并降低遗憾。作者还提出了一种 bandit 策略,这是一种基于估计参数的决策方法。当上下文是非退化时,这种策略的遗憾是次线性的,这意味着它的性能随着时间的推移会逐渐提高。此外,作者还解决了一个公开问题,并将结果扩展到了多类设置。
扫码添加小享,回复“组合优化”
免费获取全部论文及代码合集

13.Let the Flows Tell: Solving Graph Combinatorial Optimization Problems with GFlowNets. NeurlPS, 2023.
用GFlowNets解决图组合优化问题
「简述:」论文讨论了使用GFlowNets来解决组合优化(CO)问题。由于组合优化问题是NP-hard的,因此无法使用精确算法来解决,这使得它们成为应用机器学习方法的理想领域。GFlowNets是一种强大的工具,可以有效地从复合未归一化密度中进行顺序采样,并有可能在CO中实现这种解决方案搜索过程的摊销,以及生成多样化的解决方案候选。作者为不同的组合优化问题设计了马尔可夫决策过程(MDP),并提出训练条件GFlowNets来从解空间中进行采样。
14.A GNN-Guided Predict-and-Search Framework for Mixed-Integer Linear Programming. ICLR, 2023.
一种基于图神经网络的混合整数线性规划预测和搜索框架
「简述:」论文提出了一种结合机器学习和优化的混合整数线性规划预测和搜索框架,旨在有效地识别高质量的可行解。具体来说,作者首先利用图神经网络预测每个变量的边际概率,然后在预测解的适当定义球内搜索最佳可行解。作者在公开数据集上进行了广泛的实验,结果表明所提出的框架相对于MILP求解器SCIP和Gurobi在原始差距上分别提高了51.1%和9.9%的性能。
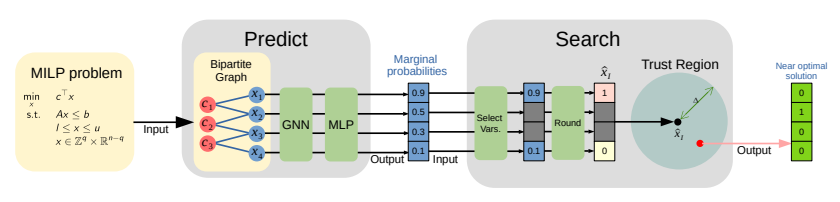
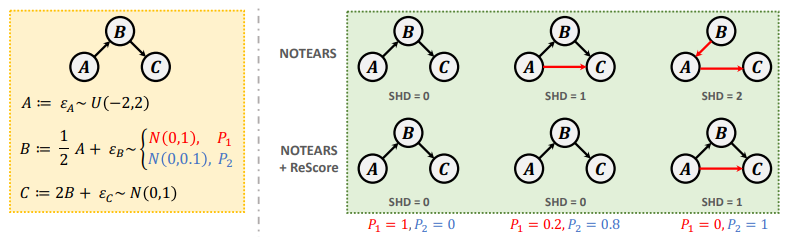
15.Boosting Causal Discovery via Adaptive Sample Reweighting. ICLR, 2023.
通过自适应样本重加权来增强因果发现
「简述:」论文介绍了一种基于重加权得分函数的因果发现方法,通过动态学习样本的自适应权重来提高因果发现的性能。作者提出了一个简单而有效的模型无关框架,称为ReScore,其中权重根据每个样本的重要性程度进行量化调整。在大量实验中,ReScore可以显著提高结构学习性能,并同时减轻虚假边的影响,适用于异构数据。
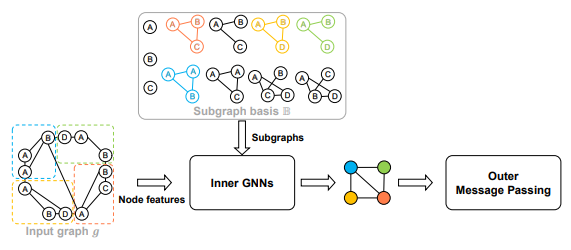
16.CktGNN: Circuit Graph Neural Network for Electronic Design Automation. ICLR, 2023.
用于电子设计自动化的电路图神经网络
「简述:」论文介绍了一种用于电子设计自动化的电路图神经网络(CktGNN),它可以同时自动化电路拓扑生成和设备尺寸调整。该方法利用嵌套图神经网络(GNN)的两级框架对电路图进行编码,提高了设计效率。作者还引入了一个开放电路基准(OCB),这是一个开源的数据集,可以用于评估和比较各种模拟电路设计的性能。实验表明,CktGNN通过基于表示的优化框架具有显著优势,为学习型开源模拟电路设计自动化铺平了道路。
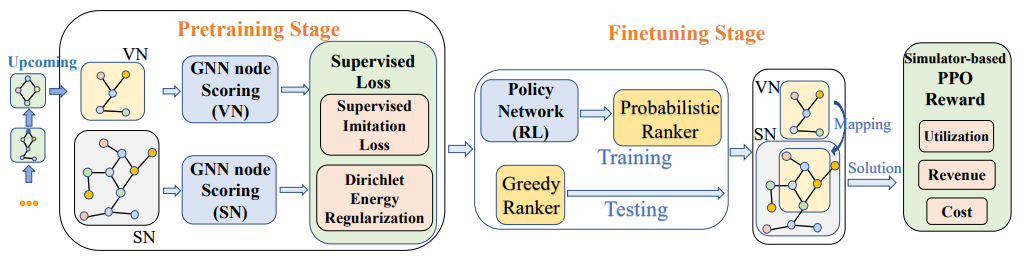
17.GAL-VNE: Solving the VNE Problem with Global Reinforcement Learning and Local One-Shot Neural Prediction. KDD, 2023.
用全局强化学习和局部单次神经预测解决VNE问题
「简述:」论文介绍了一种名为GAL-VNE的方法,用于解决虚拟网络嵌入问题。作者提出了在全局范围内使用强化学习来提高整体性能,并在每个请求的局部范围内使用一次性解决方案生成方案来提高效率。作者还提出了一种基于图神经网络的节点排序器,并使用模仿监督进行预训练和正则化。最后,使用强化学习微调GNN排序器以直接涉及商业目标。实验结果表明,该方法优于经典和基于学习的方法。
18.Two-Stage Predict+Optimize for Mixed Integer Linear Programs with Unknown Parameters in Constraints. NeurIPS, 2023.
具有未知参数约束的MILP问题的两阶段预测+优化
「简述:」论文提出了一个新的框架,称为“两阶段预测+优化”,用于处理约束优化问题中的未知参数。这个框架在训练过程中结合了优化问题的信息,以产生更好的预测质量。它不仅可以处理出现在优化目标中的未知数,还可以处理出现在约束中的未知数。作者还提供了一个通用的训练算法,可以用于所有混合整数线性程序,大大扩展了该框架的应用范围。实验结果表明,该训练框架的预测性能优于所有经典和当前最先进的方法。
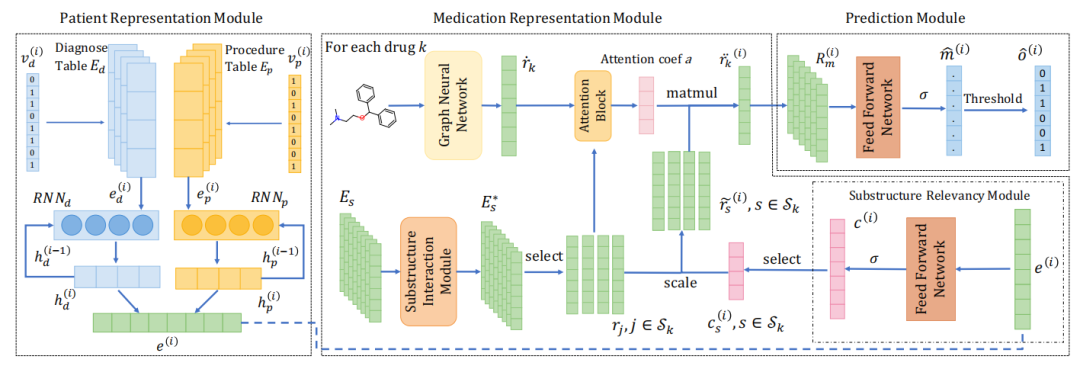
19.MoleRec: Combinatorial Drug Recommendation with Substructure-Aware Molecular Representation Learning. WWW, 2023.
结合子结构感知分子表示学习的组合药物推荐系统
「简述:」论文提出了一种新的药物推荐方法,MoleRec。该方法利用分子子结构的感知学习,通过考虑药物子结构与目标疾病之间的关系,以及子结构之间的相互作用和每个子结构对患者健康状况的影响,来推荐个性化的药物组合。这种方法能够提高推荐的准确性和安全性。在MIMIC-III数据集上的实验结果表明,MoleRec达到了新的最佳性能。
20.Learning to Optimize with Stochastic Dominance Constraints. AISTATS, 2023.
学习使用随机优势约束进行优化
「简述:」论文介绍了一种名为Light Stochastic Dominance Solver(light-SD)的方法,用于解决带有随机优势约束的优化问题。作者利用拉格朗日函数的性质,将内部优化问题转化为代理近似的学习问题,从而避免了不可操作性并得到易于处理的更新或甚至闭式解来计算梯度。作者证明了算法的收敛性,并通过实验进行了测试。该方法在从金融到供应链管理等多个代表性问题上表现出优越的性能。