降维是机器学习处理高维数据的必要手段,也是发掘数据价值的关键路径。它是一种简化复杂数据集以便更容易处理的方法,目标是将高维的数据投影或者转换到低维空间,同时尽可能保留原数据中的关键信息。
目前常用的降维技术有主成分分析(PCA)、线性判别分析(LDA)、奇异值分解(SVD)等,可以帮助我们减少计算的复杂性,提高模型的性能和效率。
这次学姐就整理了一部分数据降维相关的论文以及常用降维技术的Python示例代码来和大家分享,篇幅原因只做简单介绍,需要全部论文以及完整代码的同学看这里:
扫码添加小享,回复“降维”
免费获取全部论文+完整Python代码

降维方法论文
1.A comprehensive survey on computational learning methods for analysis of gene expression data in genomics
一项关于基因表达数据分析中计算学习方法的综合调查
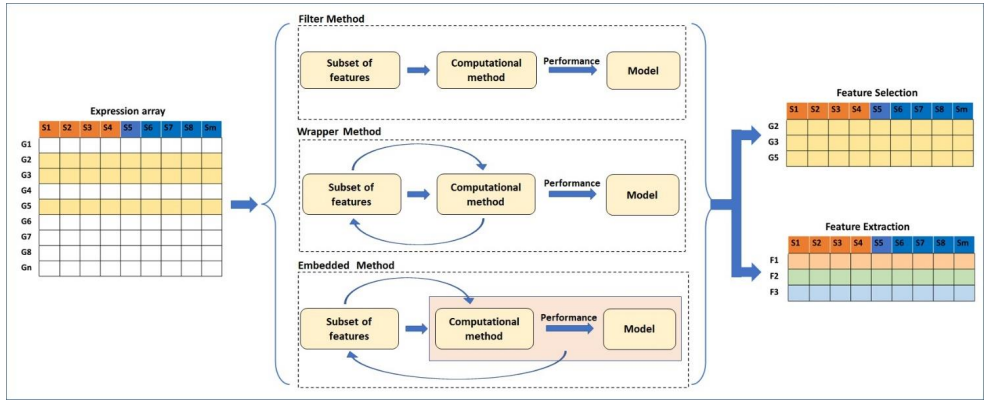
「简述:」基因表达数据分析中使用了各种统计和机器学习方法,这些方法可以处理高通量基因表达数据,进行样本分类、特征基因发现等复杂分析。本综述概述了这些计算方法,包括数据预处理、特征工程、分类与发现等方面,有助于研究人员根据分析目标选择合适的方法。总体而言,计算分析方法在基因组学和医学研究中发挥重要作用。
2.Solution of Large-Scale Many-Objective Optimization Problems Based on Dimension Reduction and Solving Knowledge-Guided Evolutionary Algorithm
基于降维和知识引导进化算法求解大规模多目标优化问题的方法
「简述:」本文提出一种基于降维和知识引导进化算法求解大规模多目标优化问题的方法。首先,对目标函数进行降维,通过聚类和聚合相关性高的目标函数,有效降低原问题的维度。此外,降维后的目标函数相关性较低,可以更好代表不同偏好。然后,提出知识引导进化算法求解转换后的问题,为得到更好的初始解集,利用镜像划分决策空间进行种群初始化,并根据每个子空间中的解的性能动态修改取样概率。同时,利用求解过程中获得的知识不断补充新的优秀个体。
3.Dimension Reduction for Spatially Correlated Data: Spatial Predictor Envelope
空间相关数据的维度约简:空间预测器信封
「简述:」预测器信封是一种回归的维度约简方法,它假设预测变量的某些线性组合对回归影响不大,与传统的最大似然估计和最小二乘估计相比,这种方法可以明显提高估计效率和预测准确性。虽然预测器信封方法已经在独立数据上进行了开发和研究,但在空间数据上还没有应用。本文将预测器信封方法应用于流行的空间模型,形成了空间预测器信封(SPE),推导了SPE的最大似然估计以及在某些假设下估计的渐近分布。
4.Unsupervised Machine Learning for Exploratory Data Analysis of Exoplanet Transmission Spectra
非监督机器学习用于系外行星透射谱的探索性数据分析
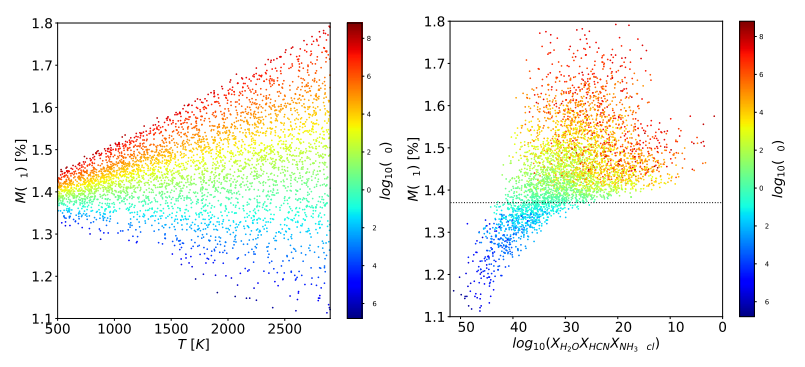
「简述:」本文利用非监督机器学习方法分析系外行星传输光谱数据。通过数据清洗、相关性分析、主成分分析等技术揭示数据内在结构,实现降维表示。实验发现不同化学成分对应数据中的清晰分支结构,可以用聚类算法自动发现,证明非监督学习是分析系外行星光谱、挖掘有用信息的有效途径。
5.Statistical Treatment, Fourier and Modal Decomposition
统计分析、傅里叶分析和模态分解
「简述:」该讲座全面介绍了图像测速法获取的数据处理方法。考虑到全面概述该领域需要单独的整门课程,讲座的范围是提供一个手把手的教程,从基本的统计分析开始,简要回顾频域和模态分析,最后介绍多尺度模态分解和非线性降维等更高级的研究课题。所涵盖的内容希望能推动新人进入该学科,同时也能让有经验的从业者感兴趣。

6.SLISEMAP: Supervised dimensionality reduction through local explanations
SLISEMAP:可解释的降维方法
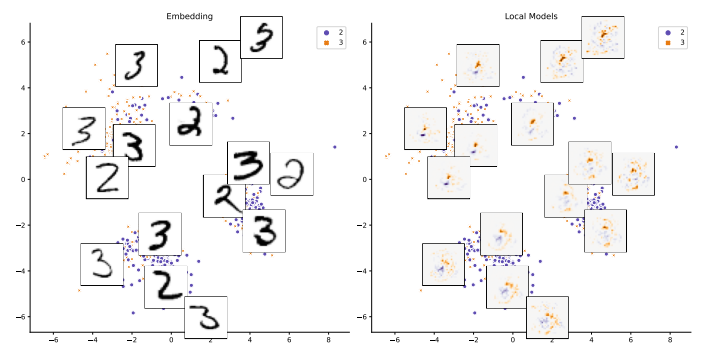
「简述:」论文提出了一种新的有监督流形可视化方法SLISEMAP,它可以同时为所有数据项找到局部解释,并建立一个通常是二维的全局可视化,使得具有相似局部解释的数据项被映射到相邻位置。作者将SLISEMAP与多种流行的降维方法进行了比较,发现SLISEMAP能利用标记数据创建局部白盒模型一致的嵌入。作者还将SLISEMAP与其他模型无关的局部解释方法进行了比较,结果表明SLISEMAP提供了可比的解释,其可视化可以更广泛地理解黑盒回归和分类模型。
7.Scaled PCA: A New Approach to Dimension Reduction
扩缩PCA:降维的新方法
「简述:」本文提出了一种新的有监督学习技术sPCA(扩缩主成分分析)用于预测。sPCA通过用每个预测变量对目标的预测斜率进行缩放来改进传统的PCA,与最大化预测变量的公共方差的PCA不同,sPCA赋予预测能力更强的变量更大权重。在一般因子框架下,论文证明在数据满足一些合适条件时,sPCA预测优于PCA预测,当这些条件不满足时,大量模拟表明sPCA仍有很大概率优于PCA。
常用降维方法
线性方法
1.PCA 主成分分析
一种常用的降维方法,基本思想是将高维数据集投影到低维空间,同时尽量保留变量的信息或方差。主要步骤包括:标准化数据,计算协方差矩阵,求特征向量,选择主成分,投影到主成分空间。PCA通过删除冗余信息实现降维,可用于可视化和降噪。

2.ICA 独立成分分析
一种重要的降维方法。将高维数据表示为成分的线性组合,并调整组合系数使各成分尽可能独立。ICA不需要知道原始混合系统,可以直接从数据中学习独立成分,利用非高斯性实现成分的独立性,有效提取数据的内在特征。ICA对数据结构的假设也少于PCA,因此可以发现PCA找不到的结构,常应用于盲源分离等领域。

3.SVD 奇异值分解
一种重要的矩阵分解方法,可用于降维和特征提取。将矩阵A分解为3个矩阵的乘积,其中Σ矩阵对角线元素为奇异值,表示A的重要特征,进行SVD后,只保留主要奇异值和向量,可以近似表达A,实现降维。SVD可以处理非方阵,应用广泛,它通过分解揭示矩阵内在特征,过滤不重要特征实现降维。

4.LDA 线性判别分析
一种常用于分类问题的降维技术。找到一个投影矩阵,可以将高维输入空间投影到低维空间,使得同类样本的投影点接近、异类样本的投影点远离,从而达到区分不同类别的目的。LDA假设不同类的数据符合高斯分布,通过最大化类间散度与最小化类内散度来确定投影方向,该方法广泛用于面部识别、情感分析等领域。

扫码添加小享,回复“降维”
免费获取全部论文+完整Python代码

非线性方法
1.MDS 多维尺度
一组用于探索数据相似性的技术。将高维对象投影到低维空间,使得投影空间中的距离结构尽可能保持原空间中的距离结构。常见的MDS方法有度量MDS、非度量MDS等,它通过降低空间维数展示对象之间的相对关系,同时保持对象间距离的一致性,广泛用于心理学和市场调查等领域的数据可视化。

2.T-SNE t-分布随机近邻嵌入
一种用于高维数据的可视化非线性降维算法。在高维空间构建点之间的相似度联合概率分布,投影到低维空间使低维相似度尽可能匹配高维分布。t-SNE能很好地保留数据全局结构,广泛用于可视化。

3.Kernel PCA 核主成分分析
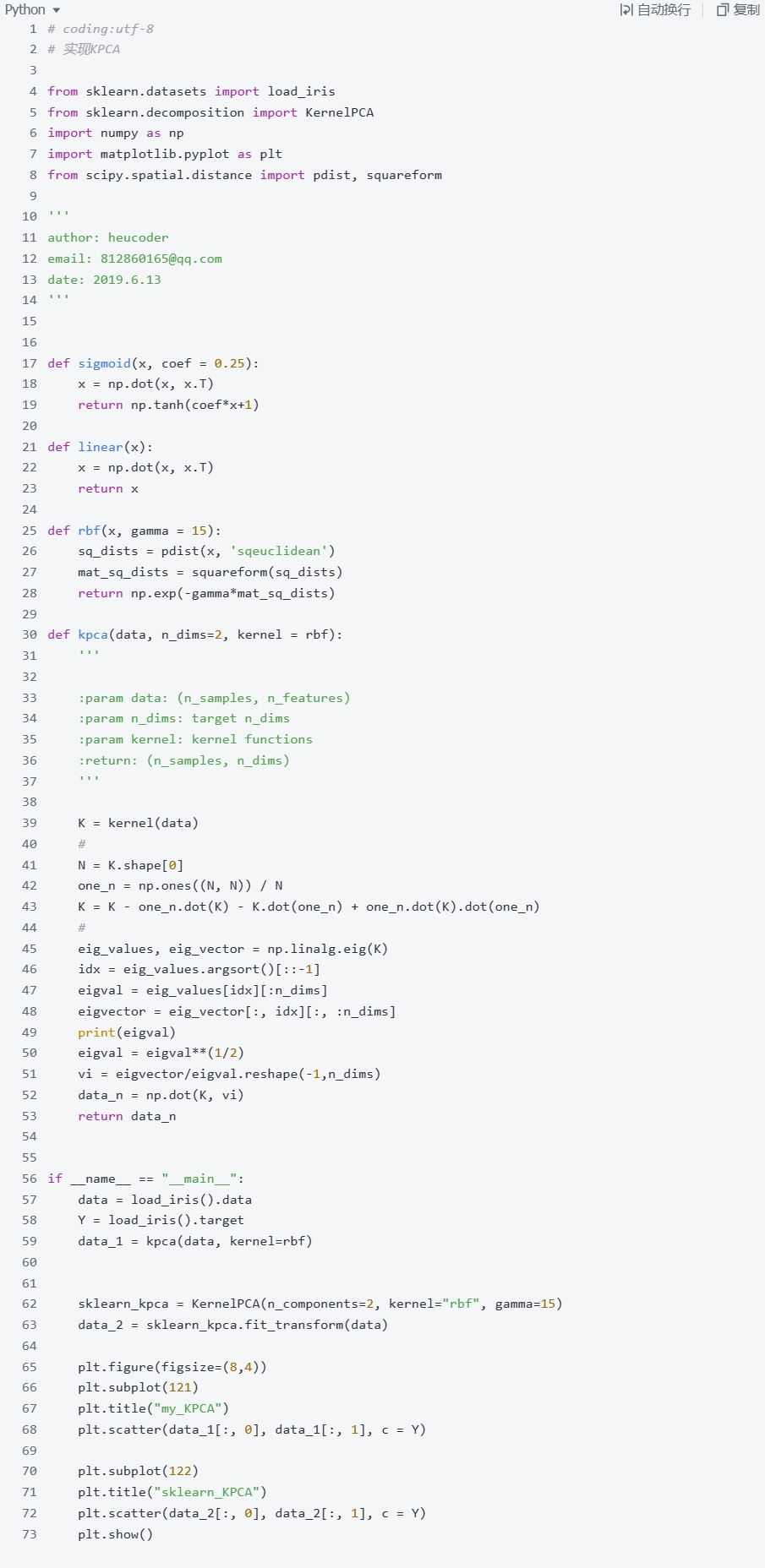
主成分分析(PCA)的非线性扩展。先将数据从原空间映射到高维特征空间,然后在特征空间进行PCA。核PCA使用核函数计算特征空间内数据点之间的点积,无需显式计算非线性映射,避免了维数灾难。常用的核函数有多项式核、RBF核等。与PCA相比,核PCA能提取数据的非线性特征,对数据分布没有线性假设,它保留了PCA的优点,如降维、去噪、可视化等,但能处理PCA无法处理的非线性情况,应用更广泛。
4.Isomap 等距映射
一种基于多维尺度思想非线性降维算法。在高维空间构建近邻距离,将距离作为低维空间的欧式距离,采用多维尺度保持距离比例关系,从而学习非线性映射。Isomap通过维持局部距离比例提取数据的全局非线性流形结构,适用于具有复杂曲面结构的数据,克服了线性降维的局限性,常用于手写数字等数据的降维与可视化。
