【ETHZ博士论文】物理启发式机器学习，185页pdf

物理启发式机器学习可以被视为将来自物理系统的结构（例如由常微分方程或偏微分方程给出的）结合到机器学习方法中，以获得具有更好归纳偏见的模型。在这篇论文中，我们为序列建模和图表表示学习领域提供了一些最早的方法示例。随后，我们显示了物理启发式的归纳偏见可以被利用来减轻每个特定领域的重要和中心问题。更具体地说，我们展示了耦合的非线性振荡器系统和哈密顿系统导致的循环序列模型能够通过减轻梯度爆炸和消失问题来处理长时间尺度的顺序交互。此外，我们严格证明了振荡器的神经系统是连续和因果算子的通用逼近器。我们还显示，从多尺度动态系统派生的序列模型不仅减轻了梯度爆炸和消失问题（从而能够学习长期依赖性），而且同样重要的是为学习（真实世界的）多尺度数据提供了富有表现力的模型。我们进一步展示了物理启发式方法对图形表示学习的影响。特别是，图形耦合的非线性振荡器系统是一种在图上学习的强大框架，允许在其上堆叠多个图神经网络（GNN）层。因此，我们证明这些系统减轻了GNN中的过度平滑问题，其中节点特征在增加的GNN层数量下指数级地收敛到相同的常数节点向量。最后，我们建议在GNN的消息传递框架中加入从底层图数据中推断出的多个速率。此外，我们利用门控函数调制的图梯度来获得自动减轻过度平滑问题的多个速率。我们在一系列多功能的合成和实际数据集上广泛测试了所有提议的方法，从图像识别、语音识别、自然语言处理（NLP）、医学应用和序列模型的科学计算，到引文网络、计算化学应用、以及文章和网站网络的图学习模型。

https://www.research-collection.ethz.ch/handle/20.500.11850/637340

在科学和工程领域中，许多问题都需要理解和建模可能的大量测量数据。典型的例子包括在物理约束下的工艺设计（例如，优化飞机翼上的升力和阻力以适应不同的运行条件）、气候模拟（例如，计算由于不同的CO2排放水平导致的全球平均海表温度）和新药设计（例如，利用已知活性结合剂的数据洞察来形成一个配体药效团模型以推断新的结构），仅举几例。因此，已经有了一长串用于模式识别和数据驱动建模的多功能方法。早期的例子包括支持向量机[Steinwart和Christmann, 2008]、常规核方法[Shawe-Taylor等人, 2004]、聚类算法[Xu和Wunsch, 2005]，以及贝叶斯方法用于概率推理[Box和Tiao, 2011]。虽然人工神经网络已经存在了很长时间，可能在其非常简单的线性回归形式（也称为最小二乘法）中存在了几个世纪，但它们目前的广泛使用主要是由于可以有效地计算它们相对于可训练参数的梯度（即反向传播算法[Rosenblatt, 1961, Rumelhart等人, 1985]）和可用的计算资源数量呈指数增长。特别是后者使得可以在大型数据集上训练更深入的模型，即，堆叠在彼此之上的多层人工神经网络，这一领域被称为深度学习[Goodfellow等人, 2016]。

深度学习现在是机器学习中最受欢迎的方法之一，对计算机科学和工程的整个子领域产生了深远的影响，如计算机视觉、自主系统和机器人技术、自然语言处理（NLP）和语音识别。深度学习的核心是深度全连接前馈神经网络（也称为多层感知器 [Rosenblatt, 1961, Werbos, 1982, Rumelhart等人, 1985]），它可以描述为多个（因此被称为“深度”）仿射变换的串联，与逐元素的非线性激活函数交替出现。更具体地说，考虑一个输入 u ∈ R^d 。一个具有N ∈ N层的深度全连接前馈神经网络（图1）可以被简洁地写为：

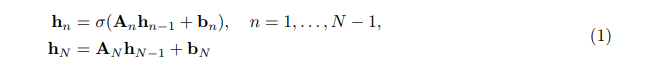
对于所有的层 n = 1, . . . , N，其中隐藏状态为 hn ∈ R^mn，权重为 An ∈ R^mn×mn−1，偏差为 bn ∈ R^mn，初始输入由 h0 = u 给出（即，m0 = d 是输入维度），并且σ表示一个非线性激活函数，例如 tanh(x) 或 relu(x) = max{0, x} 对于 x ∈ R，这是逐元素应用的。深度神经网络（1）可以通过定义一个适当的损失函数来训练，该函数测量神经网络的输出 hN 与真实数据之间的差异，然后应用基于损失函数相对于神经网络（1）的参数 {An, bn}^N_n=1 的梯度的梯度下降方法（例如随机梯度下降[Robbins 和 Monro, 1951]）。因此，梯度是使用反向传播算法有效地计算的。

尽管原则上深度全连接神经网络可以应用于任何数据集合，但深度学习在许多应用领域（如计算机视觉或NLP）的巨大成功需要对神经网络进行重大的结构变化。这些结构变化通常与“归纳偏见”相关，强调从底层数据推理出的结构。例如，计算机视觉中广泛使用的一类神经网络是卷积神经网络(CNNs) [LeCun等人，1989]，它对输入像素数据，例如图像，应用可学习的卷积。由于权重共享，CNNs被认为是移位等变的[Fukushima，1980, Bronstein等人，2021, McGreivy和Hakim，2022]。这种归纳偏见，由局部感受野[LeCun和Bengio，1995]生物学启发，使CNNs在图像数据上显著优于全连接神经网络。虽然许多神经网络结构受到生物启发，但越来越多的人对从物理学中获得灵感来构建新的机器学习模型感兴趣，这些模型可以成功地应用于物理科学中的问题。尽管在这个背景下的许多方法不具备基于物理的归纳偏见，而是将计算机视觉、NLP或图学习中的成熟模型应用于物理问题，例如[Sanchez-Gonzalez等人，2020, Vlachas等人，2020, Stachenfeld等人，2021]，但基于物理启发的归纳偏见的机器学习模型越来越多地用于物理科学中的应用。例如，等变神经网络和李代数方法在分子科学的背景下被使用，例如分子模拟[Batzner等人，2022]和分子性质预测[Satorras等人，2021]。虽然等变性是物理科学中的一个重要概念，但在建立更好的归纳偏见的神经网络结构时，人们可以潜在地利用更多的对称性和结构。例如，保存能量的守恒，如Hamilton神经网络[Greydanus等人，2019, Chen等人，2020c]，其中神经网络根据Hamilton函数参数化。这使得网络能够从数据中学习Hamilton系统，从而自动保存能量（即，Hamilton函数）。

对于神经网络的物理启发归纳偏见并不局限于物理科学中的应用。相反，最近的物理启发机器学习方法在深度学习的许多传统领域都有应用。例如在生成建模中，扩散模型[Yang等人，2022]是最先进的。这些模型利用一个物理过程，即扩散，逐渐地用随机噪声损坏输入数据。一旦训练完成，新数据可以通过反转扩散过程生成。由于这种方法基于物理过程，所以在这个背景下的许多模型从物理系统中获得启示，以构建具有更好的归纳偏见的扩散模型[Dockhorn等人，2021, Lai等人，2022, Salimans和Ho，2021]。另一个例子包括图表示学习，其中越来越多使用物理启发的图神经网络(GNNs)。例如，在基础GNN操作（所谓的消息传递[Bronstein等人，2021]）中引入各向异性扩散[Chamberlain等人，2021b]、渐变流[Di Giovanni等人，2022]、反应-扩散方程[Choi等人，2022]或双曲偏微分方程(PDEs) [Eliasof等人，2021]，仅举几例。

在这篇论文中，我们提供了几个最早的基于物理启发的机器学习模型的例子。更具体地说，我们提供了由非线性耦合振荡器系统、(时依赖的)哈密尔顿系统和多尺度动力系统启发的循环序列模型。我们随后展示了这些模型，由于其基于物理的归纳偏见，展现出了非常有利的特性，例如处理序列数据中的长期相互作用，或者在真实世界的数据集上提高表现力。此外，我们提供了基于图表示学习的物理启发模型，这些模型受到图-动力系统的启发，即图-耦合振荡器以及多速率图-动力系统。我们进一步为这些模型证明了各种有益的特性，例如使用GNNs的图表示学习中的中心问题，即过度平滑[Nt和Maehara，2019, Oono和Suzuki，2020]，以及处理异性(大规模)图数据集。

这篇论文的第一部分从受物理启发的角度重点讨论序列建模。我们从第一部分开始，介绍序列模型，即 Transformers 和递归神经网络 (RNNs)。随后，我们提出了三种新颖的、受物理启发的 RNN 架构。我们提议的第一个架构被称为 Coupled Oscillatory RNN (coRNN)。我们在第二章介绍 coRNN 并在第 2.2 节为所提议的模型提供严格的理论分析。此外，我们在第 2.3 节为 coRNN 提供了广泛的实证评估。本章基于[Rusch 和 Mishra, 2021a]的出版物。

我们进一步在第三章介绍 Undamped Independent Controlled Oscillatory RNN (UnICORNN)。同样，我们在第 3.2 节提供了严格的分析，并在第 3.3 节对所提议的 UnICORNN 架构进行了广泛的实证评估。本章基于[Rusch 和 Mishra, 2021b]的出版物。在第四章，我们通过引入神经振荡器来推广 coRNN 和 UnICORNN。随后，我们严格地证明神经振荡器是通用的。这一章基于[Lanthaler 等人，2023]的预印本。

在第一部分的最后一章，即第五章，我们提出了 Long Expressive Memory (LEM)，这是一种用于学习长期依赖关系的表达性递归序列模型。在第 5.2 节，我们严格地证明了所提议的 LEM 的梯度稳定性，并显示 LEM 是普遍 (Lipschitz 连续) 多尺度动力系统的通用逼近器。此外，我们展示 LEM 仿真常微分方程 (ODEs) 的异构多尺度方法。最后，在第 5.3 节，我们为所提议的 LEM 架构提供了各种多功能的数值实验。本章基于[Rusch 等人，2022b]的出版物。

这篇论文的第二部分涉及受物理启发的图表征学习。我们开始第二部分，介绍现代图神经网络和底层的信息传递框架。此外，我们概述了当前框架的重要限制，特别是深度 GNNs 中的过度平滑问题（过度平滑的定义基于[Rusch 等人，2023]）。随后，我们提议了两种受物理启发的信息传递框架。我们提议的第一种方法在第七章被称为 Graph-Coupled Oscillator Network (GraphCON)。我们进一步在第 7.2 节为 GraphCON 提供了严格的分析，并在第 7.3 节进行了广泛的实证评估。这一章基于[Rusch 等人，2022a]的出版物。这一部分的最后一章，即第八章，介绍了 Gradient Gating 框架 (G2)。我们在第 8.2 节为所提议的 G2 框架提供了理论洞察，并在第 8.3 节在各种（大规模）图数据集上测试其性能。这一章基于[Rusch 等人，2022a]的出版物。最后，我们在第九章结束这篇论文。

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复或发消息“P185” 就可以获取《【ETHZ博士论文】物理启发式机器学习，185页pdf》专知下载链接