经过多代更迭,我们目前较为推荐的方式为双排名法。即针对每只个券计算:
其价格在全体转债中的排名(从小到大),记做RankClose
2. 其溢价率在全体转债中的排名(从小到大),记做RankPrem
3. 将RankClose 与 RankPrem加总,记做TR,并在每一个换仓日取TR靠前的50%品种。
我们的测算实现很简单,首先根据上述的择券标准,以及在frameStrategy中既定的格式,写出择券逻辑函数。注意,该函数有五个固定参数,但仅data(数据库变量)、date(假设的日期)、codes(当日可用的转债代码)常用,allCodes(全部历史转债代码)和dfAsset(账户情况)相对不常用。我们将择券函数,测算以及作图实现均列于下方。
def easyBall(data, allCodes, date, codes, dfAsset):
TR = data.Close.loc[date, codes].rank()
TR += data.ConvPrem.loc[date, codes].rank()
return TR[TR < TR.quantile(0.5)].index
# 注意下面是将这个函数名作为输入变量,放入测算框架中,目前默认等权、换仓频率一个月,但均可另行设置
测算结果 = cb.frameStrategy(data, selMethod=easyBall)
# 简易作图, 指定
测算结果.plot(figsize=(12, 5))
利用正股因子时,需要将正股因子映射到转债上。我们此前介绍过一个辅助函数st.factor,如下所示。
def factor(cbCodes, fields, date, other=''):
'''得到单个因子或者因子组的函数,基于w.wss
cbCodes, fields, date, other=''
'''
if len(cbCodes) == 0:
return pd.Series()
if other:
other = ';' + other
_,dfUnderlying = w.wss(",".join(cbCodes), "underlyingcode", usedf=True)
uniStock = list(set(dfUnderlying.UNDERLYINGCODE))
date = pd.to_datetime(date).strftime("%Y%m%d")
_, dfRaw = w.wss(','.join(uniStock), fields, "tradeDate="
+date+other, usedf=True)
return dfUnderlying.merge(dfRaw, left_on='UNDERLYINGCODE', right_index=True).iloc[:,1]
下面以ROE为例,我们测算一个轮动正股ROE大于10%的策略。
def ROE策略(data, allCodes, date, codes, dfAsset):
srsROE = factor(codes, "fa_roenp_ttm", date)
return srsROE[srsROE > 10].index
ROE测算 = cb.frameStrategy(data, selMethod=ROE策略)
实际上,在我们提出策略框架的这三年时间里,客户问到的、需求更多的仍是简单策略的实际情况。一方面简单策略容易实现,另一方面对于更多投资者而言,则是希望看到“某某类型的转债表现如何?”,并依据此制定计划,而不是仅寄希望于机器人能够选出好的个券——即便,目前来看一些精巧的模型, 能够做出很好的效果来。下面我们分门别类地展示。
这两个结论都是显然的,小盘强于大盘、低等级强于高等级。其中小盘策略强于大盘一方面存在风格暴露的回报,但也要注意,小盘在正股弹性、公司主动性等方面天然存在优势——当然,这里一定程度上也有流动性溢价率的成分在。显然我们一般也并不推荐纯基于规模因子的策略。
资料来源:Wind,中金公司研究部;注:纵轴为策略净值,起始日为2017年12月29日
而信用等级上的结果已经逐渐被投资者接受,更深层次地看,排除与规模类似的理由后,我们也要知道,本质上:是评级与转债的风险并不匹配,并不适用传统的分析方法——否则我们难以解释,目前甚至B级别以下的转债也并未出现过违约,而即便是AAA的信用债确仍有一定违约风险。
资料来源:Wind,中金公司研究部;注:纵轴为策略净值,起始日为2017年12月29日
更严格来说,即便考虑波动、回撤,用类似夏普、卡玛的指标衡量,评级与策略效果的关系也是单调递减的。因此在过去的多年研究中,我们一直不建议投资者在非受迫的情况下考虑评级。
一般以“平价 / 债底”来衡量股债性,我们习惯取0.8以内为债性、1.2以上为股性,居中为平衡性。这里为了避免债性品种上涨后太快进入股性或者平衡性,导致算法的失败,我们调整了换仓时间参数,比如设为42(即2个月左右)。
资料来源:Wind,中金公司研究部;注:纵轴为策略净值,起始日为2017年12月29日
显然,与评级越低越好不同的是,股、债、平衡性存在一定取舍关系,综合来看平衡性品种在夏普比例等方便更占优——这也是因为它们的“期权性”普遍更胜一筹。
即以限制价格、溢价率等指标为主的简单策略,而由于这些策略的高容量,往往作为更复杂的策略或者择券的“基底”。这里我们能看到一些结果,由于时间已有接近5年,具备较强的参考性。对投资者来说,选择一个“基底”有些类似于在转债市场上选择一个“赛道”。不难看到的结论是:
1. 如我们在《偏债不佳之惑》中总结的,低价类策略的实施往往可以降低波动,但无法显著限制最大回撤。因为“最大”回撤往往由于一些偏极端的情形,仅寄希望于依靠债底来保存实力可能并不现实;
2. 不难想象的是,始终以低溢价率为纲,在绝对回报上战胜指数及市场平均水平不难——当然前提是20%以上的最大回撤。但仔细观察可以发现,以卡玛比率来看,其性价比仍然要高于低价类的策略——这个差距一定程度上来自正股。因为低价品种并非“正股中性”,一般而言其正股长期动量偏弱、弹性略弱,低溢价品种则相反。一定程度上,低价和低溢价本身也是一个结果——正股走势导致的结果。
3. 但我们文章开头介绍的EasyBall,在策略容量很大的情况下,可能得到安全性不输低价、收益性与低溢价策略差之毫厘的效果。但我们也能看到,这一策略并不“单调”——取30%为参数时,效果并不比50%强。我们的理解是:这个策略的优势在于剔除高估值,而“更低”却不意味着“更好”。
4. 当然,最下面的“双低_120元与15%溢价率”显得效果更好,但其适用性则相对有限,因为代价是:1)相对不高的“出勤率”——有的时段甚至没有选择;2)相对很小的策略容量——有的品种即便入选,也往往是机构投资者无法买入的品种。
基于股票的因子自然有很多,我们在此仅展示部分常用、适用范围本身也比较广的因子测试结果。下面的结果均为取某个方向前30%的品种,我们认为如果一个因子是大体上有显著价值的,那么其不应该在取前30%时还与总体样本无统计差异,详见下图。而一些有意思的结论是:
1. 正股因子的显著性,绝大多数要弱于转债的估值因子——即便我们遍历数据库,在“取前30%”的假定下(排除容量极低的策略),没有任何一个在夏普、卡玛等综合评估指标上,能接近基础的EasyBall。显然,转债因子对转债的作用更加直接,这也是为何我们一向反对诸如“虽然某某转债溢价率很高、价格也很高,但由于强烈看好正股,于是买入转债”——不排除个别样本可能有回报,但强行用主观的“看好”来对抗稳定的统计大数定律,还是会略显勉强。
2. 当然这并非说股票因子无用,而是对于策略的性质刻画,显然转债因子更加有效,因此我们对正股因子的考虑,主要在“是否有收益增强"上。
3. 相对来说,就"是否有收益增强"来说,不考虑市值(与前述规模有共线性),那么:
1)如近些年的经验、理论上的推演,动量、波动类因子相对容易做出成绩;
2)在估值类指标整体效率一般的情况下,市值比现金流相对有效;
3)盈利预期变化有正面贡献,以6个月为尺度的效果要比1个月要好;
4)考虑成长性的话,5年复合比短期增长更有说服力。
显然,单一股票因子显著性普通,因而股票的强化效果与转债因子是否存在“化学反应”,就变得比较重要。而与转债因子策略进行结合,如仍需逐个手动写入,工作量将会几何级别提升。这里我们提供了一个简单的“合成”工具,用以拼接转债策略与股票因子策略。目前设计的“合成”方式有两种:顺序过滤,以及取交集。如下图所示:
这里我们加入一个新的功能synthesis,以便未来调用,逻辑如下。使用方式也十分简单,此处不赘述。
class synthesis(object):
def __init__(self, obj, lstStrategy, kind="Serial"):
'''
obj : 数据库变量,cb_data().
lstStrategy : list, tuple, OrderedDict
策略列表,函数名即可.
kind : str, optional
可以是Serial 或者Intersection. The default is "Serial".
'''
obj.strategys = lstStrategy
if kind == "Serial":
def myFunc(data, ac, date, codes, ass):
for s in obj.strategys:
codes = s(data, ac, date, codes, ass)
if len(codes) == 0:
return []
return codes
elif kind == "Intersection":
def myFunc(data, ac, date, codes, ass):
ret = set(codes)
for s in obj.strategys:
t = s(data, ac, date, codes, ass)
ret = ret.intersection(t)
return list(ret)
else:
raise ValueError("kind must be one of Serial or Intersection")
self.func = myFunc
以EasyBall和高60日波动为例,我们列举其使用方法如下。这里我们使用kind的默认参数,即按照list的顺序,先选择EasyBall,再在其中样本选择高动量,投资者亦可尝试其他因子和合成方式。
def easyBall(data, allCodes, date, codes, dfAsset):
TR = data.Close.loc[date, codes].rank()
TR += data.ConvPrem.loc[date, codes].rank()
return TR[TR < TR.quantile(0.5)].index
def 动量250日(data, ac, date, codes, ass):
date = _offsetDate(obj, date)
srs = st.factor(codes, "TECH_REVS250", date)
return srs[srs > srs.quantile(0.7)].index
合成策略 = synthesis(obj, [easyBall, 动量250日]).func
合成策略测算 = cb.frameStrategy(obj, selMethod=合成策略, roundMethod=42)
合成策略测算.plot(figsize=(10,5))
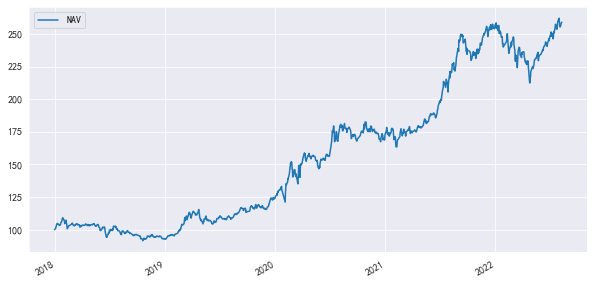
我们也将上述提到的因子,与EasyBall之间结合的策略的过去5年测算效果,列于下方,供投资者参考。简而言之,盈利预期变化、毛利率、动量、波动等,均能一定程度上在EasyBall的基础上进一步提升收益以及卡玛比例。
这个问题的关键其实不在于预测是会发生赎回,而在于如何应对好提前赎回条款触发。过去我们的回测多进行月度调仓,在这期间如果某只转债涉及强赎触发,组合收益可能存在一定削减。因此在这里,我们希望能够尽可能仿照实际情况,当转债公告赎回后将其剔除,并对剩余资金做处理。
资料来源:Wind,中金公司研究部注:此处所指的赎回公告指的是明确赎回登记日的那版赎回公告发布日期,而不是触发赎回当日公司所作的公告,因此大部分转债此时溢价率已开始明显被压降,回落空间从统计上来看虽有但并不大
明确我们要做的工作后,我们实际的程序逻辑很直白——先获取每日更新的转债赎回情况列表,对照我们当日持仓组合,将其中在前一交易日公告赎回的转债进行剔除。再根据现有的转债列表,我们再进行仓位的平衡或留空。以下程序实现能比较直观解释我们的各项步骤。
def _checkCall
(database, dfRet, dfAssetBook, trade_dt, reBalanced):
'''
:param database: 存储转债标化数据的数据库
:param dfRet: 存储策略净值表现的dataframe
:param dfAssetBook: 存储当期策略选择的券及权重
:param trade_dt: 交易日
:param reBalanced: 是否对于仓位进行再平衡
:return: 策略新选择的券与对应权重
'''
# 获取赎回公告,index为各已公告赎回的转债代码,announceDate列表示赎回公告发布时间
if not hasattr(database, 'callTable'):
database.callTable = getCallTable(database.tickers)
# 如果为开仓日,则不做处理
if trade_dt == dfRet.index[0]:
return dfAssetBook
else:
# 将日期常数化后,将已公告赎回的转债剔除
tradeInt = int(pd.to_datetime(trade_dt).strftime('%Y%m%d'))
called = database.callTable[database.callTable['announceDate'] < tradeInt].index
reSel = [ticker for ticker in dfAssetBook.index if ticker not in called]
if reBalanced & (len(dfAssetBook) != len(reSel)):
reWgt = _getWeight(database, reSel, trade_dt, weightMethod)
# dfAssetBook是我们每期换仓时持有转债的表格,_getWeight是重新再对仓位进行平衡
dfAssetBook = pd.DataFrame(index=reSel, columns=['costPrice', 'w', 'betas'])
dfAssetBook['costPrice'] = 100.
dfAssetBook['w'] = reWgt
else:
dfAssetBook = dfAssetBook.loc[reSel]
return dfAssetBook
我们以下做了简单的验证,发现剔除赎回能有效减少因为接近赎回到期日,而造成后续的损失。但这一动作并不必然会影响我们策略的回报回撤比,同时对于部分低溢价导向策略其效果会相对有限。
本文摘自:2022年8月12日已经发布的《转债量化策略框架2.0与Python实现》
杨 冰 SAC执业证书编号:S0080515120002;SFC CE Ref: BOM868
房 铎 SAC执业证书编号:S0080519110001
罗 凡 SAC执业证书编号:S0080522070003
陈健恒 SAC执业证书编号:S0080511030011;SFC CE Ref: BBM220