给学徒们收集整理了几套带GitHub源代码的文献图表合辑，让优秀者一点一滴拆解开来分享给大家。（全部的代码复制粘贴即可运行，欢迎尝试以及批评指正），前面的目录是：

下面是去年实习生的分享

数据和代码都是在：数据与代码全部公开在https://github.com/sangho1130/KOR_HCC 大家自己去下载哦！

t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。并且，t-SNE是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。相对于PCA来说，t-SNE可以说是一种更高级有效的方法，

下面来实现Fig.2d的t-SNE图

文章来源："Preoperative immune landscape predisposes adverse outcomes in hepatocellular carcinoma patients with liver transplantation" (2021,npj Precision Oncology)，数据与代码全部公开在https://github.com/sangho1130/KOR_HCC。

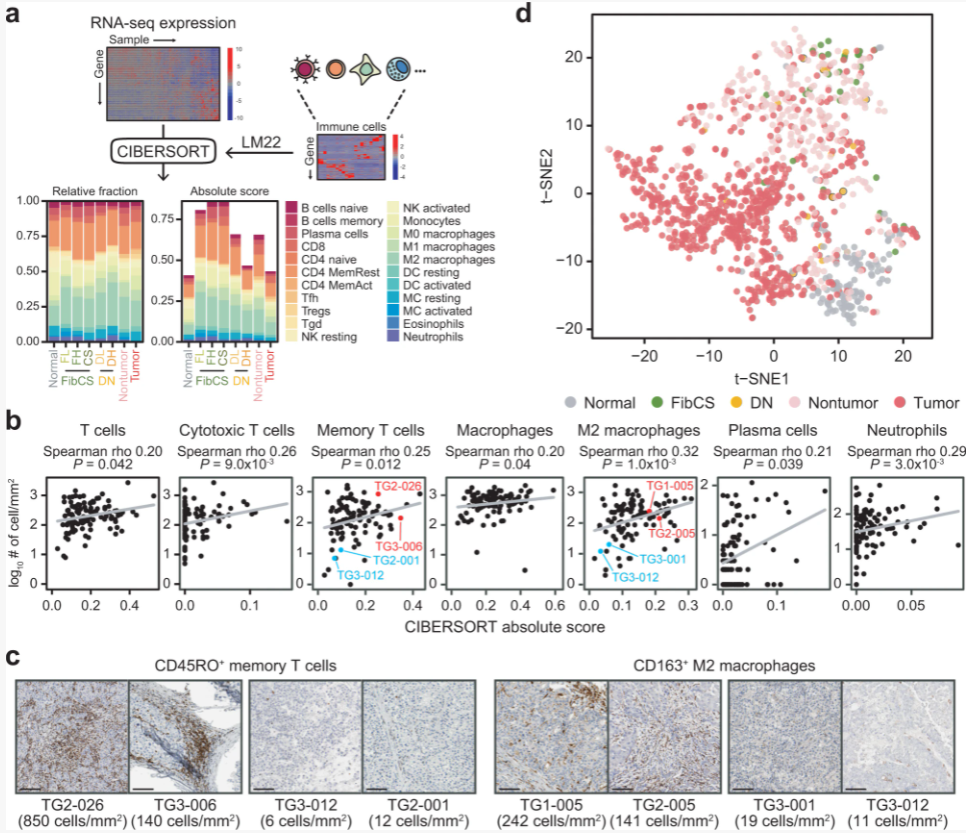
这里作者根CIBERSORT免疫分数进行t-SNE分析，将样本投影到二维坐标系。发现FibCS（肝纤维化）和DN（dysplastic nodule，癌前病变即发育不良结节）样本没有聚集在一起，并且与非肿瘤样本混合起来，且与肿瘤样本明显分离，推断出免疫浸润情况可以识别出癌前阶段的显著特征。

一、安装R包

主要用到Rtsne包，首先安装R包

install.packages("Rtsne") # Install Rtsne package from CRAN

也可以通过github安装

if(!require(devtools)) install.packages("devtools") # If not already installed
devtools::install_github("jkrijthe/Rtsne")

二、数据载入

rm(list = ls())
library(Rtsne)
library(ggplot2)
#library(rgl)
library(plyr)

table data #  Rtsne() 在运行时默认会进行重复数据检测，如果不事先去除重复样本则会报错。
# data.uni = unique(data) # 去除重复数据
dataGrade data$Grade 
head(data)
head(dataGrade)

二、tsne分析

基础用法如下：

tsne_out  data,
 dims = 2,
 pca = FALSE,
 perplexity = 10,
 theta = 0.0,
 max_iter = 1000,
 verbose = F
)

参数解释：

data 用于降维的原始数据，其中行代表特征，列代表样本;
dims参数设置降维之后的维度，默认值为2;
pca 逻辑型变量，规定是否在t-SNE前预先进行PCA分析，默认为True。(pca参数表示是否对输入的原始数据进行PCA分析，然后使用PCA得到的topN主成分进行后续分析，t-SNE算法的计算量是特别大的，对于维度较高的数据数据，先采用PCA降维可以有效提高运行的效率，默认采用top50的主成分进行后续分析，当然也可以通过initial_dims参数修改这个值。)
perplexity 这个值是一个正整数，且满足 3*perplexity < nrow(data) - 1 。作为计算数据点相似度的参数， perplexity 可以简单理解为对每个点具有的近邻数量的猜测，代表了平衡数据的局部和全局方面之间的程度，对生成的图像有复杂的影响。一般来说，随着perplexity 值的增加，形状越来越清晰。
theta 计算速度与精确度之间的权衡，范围在0~1之间，越接近0越精确，默认0.5。这个参数影响最终计算结果，可以根据图像效果进行选取。
max_iter 迭代次数，默认为1000，过小则结果未完全收敛，过大则浪费计算量。
verbose 是否输出计算进度，在数据集较大的时候比较实用。

运算完成之后，结果保存在tsne这个对象中

说明书：https://cran.r-project.org/web/packages/Rtsne/Rtsne.pdf

实际分析：

# 由于t-SNE的结果具有随机性，因此在计算前必须设定固定的随机数种子，否则结果无法重复。
set.seed(0011) # 设置随机数种子
tsne

结果是一个有14个元素的list，其内容如下：

str(tsne)

# 其中的Y就是降维之后的二维空间对应的数据点，可以根据这个值进行可视化
scores rownames(scores) colnames(scores) head(scores)

三、设置分组

作者这个数据比较特殊，他是在分析完tsne之后再添加分组




    
# 新增grade列，为数据的分组
scores # mapvalues直接对数据的元素进行一一转换
scores$disease                             from = c('Catholic_Normal', 'GTEx',
                                     'Catholic_CS', 'Catholic_FH', 'Catholic_FL', 'Catholic_DL', 'Catholic_DH', 
                                     'Catholic_T1', 'Catholic_T2', 'Catholic_T3T4', 'Catholic_Mixed',
                                     'GSE77509_Nontumor', 'GSE77509_Tumor', 'GSE77509_PVTT', 
                                     'Riken_Nontumor', 'Riken_T1', 'Riken_T2', 'Riken_T3T4',
                                     'TCGA_Nontumor', 'TCGA_T1', 'TCGA_T2', 'TCGA_T3T4'), 
                            to = c('Normal', 'Normal',
                                   'FibCS', 'FibCS', 'FibCS', 'DN', 'DN', 
                                   'Tumor', 'Tumor', 'Tumor', 'Tumor',
                                   'Nontumor', 'Tumor', 'Tumor', 
                                   'Nontumor', 'Tumor', 'Tumor', 'Tumor',
                                   'Nontumor', 'Tumor', 'Tumor', 'Tumor'))
# 转成因子，并设置顺序
scores$disease head(scores)

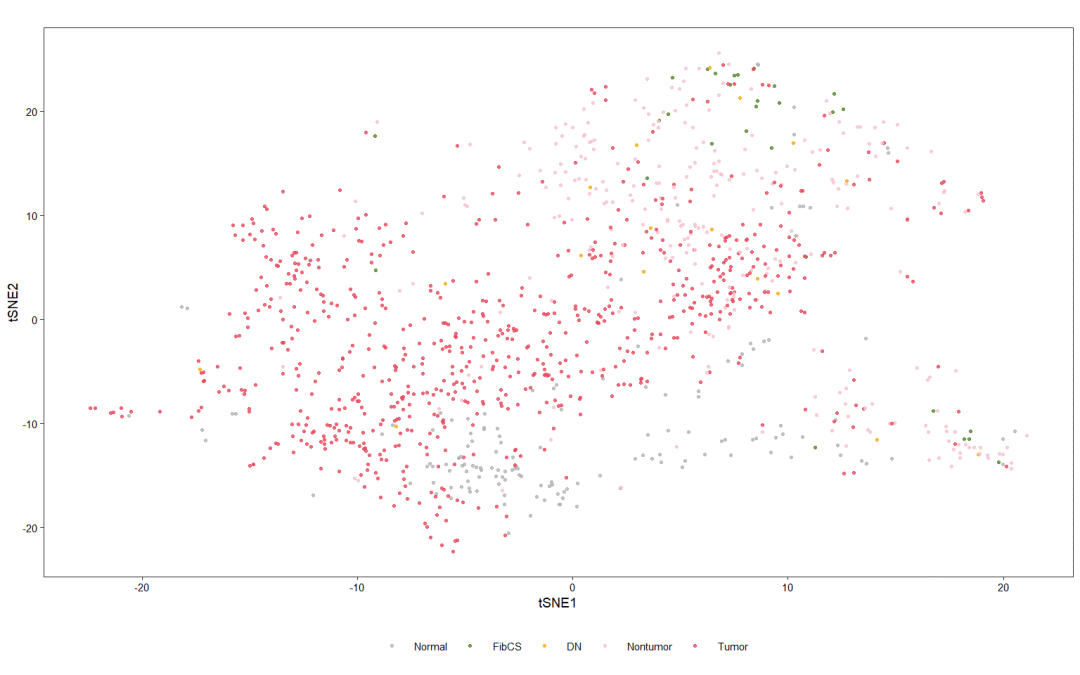
四、绘图

又回到我们散点图的画法了

plt   geom_point(size = .5, alpha=0.8) + 
  scale_colour_manual(name="", values = c('Normal' = '#b3b2b2', 'FibCS' = '#528828', 'DN' = '#f2ae0e', 'Nontumor' = '#f5c2cf', 'Tumor' = '#e8495b')) +
  theme_bw(base_size = 7) + 
  theme(axis.text = element_text(colour = 'black'), # 轴刻度值
        panel.grid = element_blank(), # 空白背景
        legend.position="bottom") + # 注释位置
  labs(title =  '')
plt
# ggsave('../results/Figure 2D 2dim.pdf', units = 'cm', width = 8, height = 6)
# scores.w # write.table(scores.w, '../results/Figure 2D tSNE projection.txt', quote = F, row.names = F, col.names = T, sep = '\t')

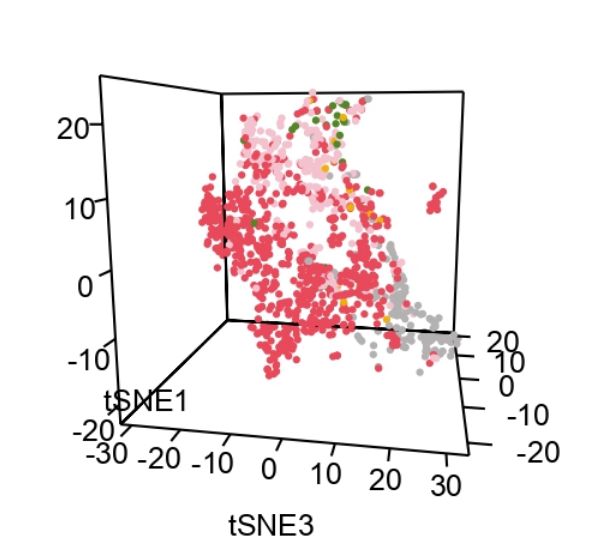
五、交互式3D图

这个就更炫酷了！

参考：http://www.sthda.com/english/wiki/a-complete-guide-to-3d-visualization-device-system-in-r-r-software-and-data-visualization

https://cran.r-project.org/web/packages/rgl/vignettes/rgl.html

library(rgl)
scores head(scores)
# 添加颜色
clustercolors table(clustercolors)

# 绘图
plot3d(scores[, 1:3], # xyz轴数据
       col = clustercolors, # 颜色
       type = 'p', # 形状。'p'表示点，'s'表示球面，'l'表示线，'h'表示从z = 0开始的线段，'n'表示空的线段
       box = FALSE, # 外面是否绘制出箱子
       size = 3) # 点的大小
# 加装饰
decorate3d(main = '', # 标题
           box = FALSE, # 外面是否绘制出箱子
           xlab = '', ylab = '', zlab = '') # xyz轴标签
# 加注释
legend3d("right", # 注释位置
         legend = c('Normal', 'FibCS', 'DN', 'Nontumor', 'Tumor'), # 注释内容
         col = c('#b3b2b2', '#528828', '#f2ae0e', '#f5c2cf', '#e8495b'), # 注释颜色
         pch = 16, # 符号标识 
         cex=0.5, # 大小
         inset=c(0.01)) # 相对位置，第一个参数为横轴，第二参数为纵轴
view3d(theta = 280, phi = 10, zoom = .9) # 将视点旋转到合适的位置
# 保存3D图
# rgl.postscript(filename = "../results/Figure 2D 3dim.pdf", fmt = "pdf", drawText = TRUE)
# rgl.close()