
文章目录
前言
1 优化的目标
2 深度学习中的优化挑战
2.1 鞍积分
2.2 消失渐变
3 凸性
3.1 convex set
3.2 凸函数
4 局部极小值是全局极小值
5 约束
6 总结
参考
前言
优化器或者优化算法,是通过训练优化参数,来最小化(最大化)损失函数。损失函数是用来计算测试集中目标值Y的真实值和预测值的偏差程度。
为了使模型输出逼近或达到最优值,我们需要用各种优化策略和算法,来更新和计算影响模型训练和模型输出的网络参数。这种算法使用各参数的梯度值来最小化或最大化损失函数E(x)。最常用的一阶优化算法是梯度下降。函数梯度:导数dy/dx的多变量表达式,用来表示y相对于x的瞬时变化率。往往为了计算多变量函数的导数时,会用梯度取代导数,并使用偏导数来计算梯度。梯度和导数之间的一个主要区别是函数的梯度形成了一个多维变量。因此,对单变量函数,使用导数来分析;而梯度是基于多变量函数而产生的。二阶优化算法使用了二阶导数(也叫做Hessian方法)来最小化或最大化损失函数。这种方法是二阶收敛,收敛速度快,但是由于二阶导数的计算成本很高,所以这种方法并没有广泛使用。主要算法:牛顿法和拟牛顿法(Newton's method & Quasi-Newton Methods)
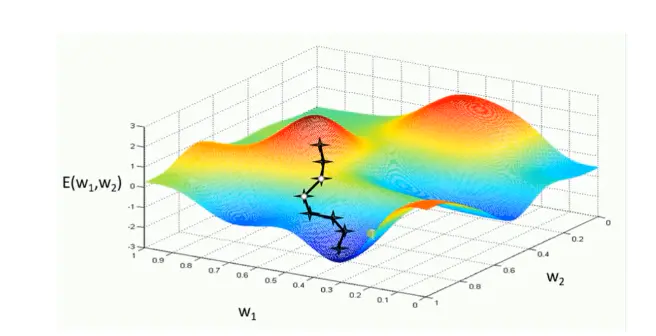
1 优化的目标

优化提供了一种最大限度地减少深度学习损失功能的方法,但实质上,优化和深度学习的目标是根本不同的。前者主要关注的是尽量减少一个目标,而鉴于数据量有限,后者则关注寻找合适的模型。例如,训练错误和泛化错误通常不同:由于优化算法的客观函数通常是基于训练数据集的损失函数,因此优化的目标是减少训练错误。但是,深度学习(或更广义地说,统计推断)的目标是减少概括错误。为了完成后者,除了使用优化算法来减少训练错误之外,我们还需要注意过度拟合。
def f(x):
return x * torch.cos(np.pi * x)
def g(x):
return f(x) + 0.2 * torch.cos(5 * np.pi * x)
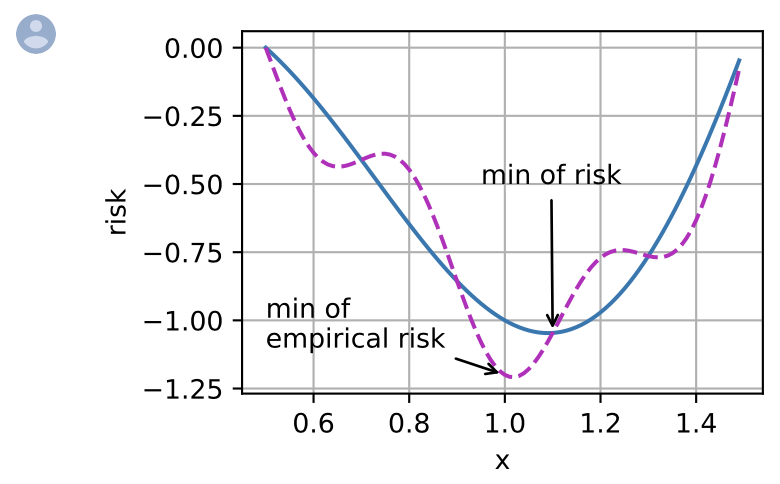
下图说明,训练数据集的最低经验风险可能与最低风险(概括错误)不同。def annotate(text, xy, xytext): #@save
d2l.plt.gca().annotate(text, xy=xy, xytext=xytext,
arrowprops=dict(arrowstyle='->'))
x = torch.arange(0.5, 1.5, 0.01)
d2l.set_figsize((4.5, 2.5))
d2l.plot(x, [f(x), g(x)], 'x', 'risk')
annotate('min of\nempirical risk', (1.0, -1.2), (0.5, -1.1))
annotate('min of risk', (1.1, -1.05), (0.95, -0.5))
2 深度学习中的优化挑战

深度学习优化存在许多挑战。其中一些最令人恼人的是局部最小值、鞍点和消失的渐变。让我们来看看它们。
对于任何客观函数 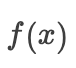 ,如果
,如果 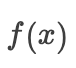 的值
的值 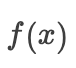 在 附近的任何其他点小于
在 附近的任何其他点小于 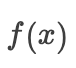 的值,那么
的值,那么 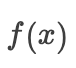 在 附近的任何其他点的值小于
在 附近的任何其他点的值小于
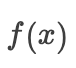 ,那么
,那么 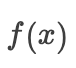 可能是局部最低值。如果
可能是局部最低值。如果 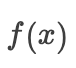 的值为
的值为 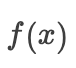 ,为整个域的目标函数的最小值,那么
,为整个域的目标函数的最小值,那么 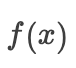 是全局最小值。
是全局最小值。x = torch.arange(-1.0, 2.0, 0.01)
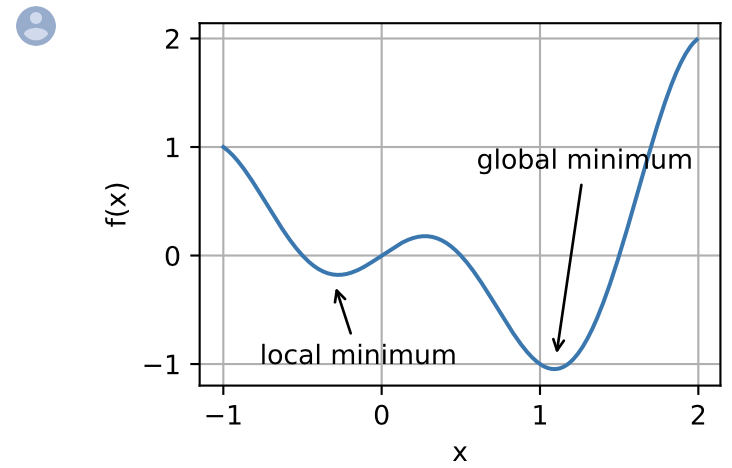
d2l.plot(x, [f(x), ], 'x', 'f(x)')
annotate('local minimum', (-0.3, -0.25), (-0.77, -1.0))
annotate('global minimum', (1.1, -0.95), (0.6, 0.8))
2.1 鞍积分
除了局部最小值之外,鞍点也是梯度消失的另一个原因。* 鞍点 * 是指函数的所有渐变都消失但既不是全局也不是局部最小值的任何位置。考虑这个函数 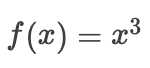 。它的第一个和第二个衍生品消失了
。它的第一个和第二个衍生品消失了 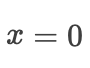 。这时优化可能会停顿,尽管它不是最低限度。
。这时优化可能会停顿,尽管它不是最低限度。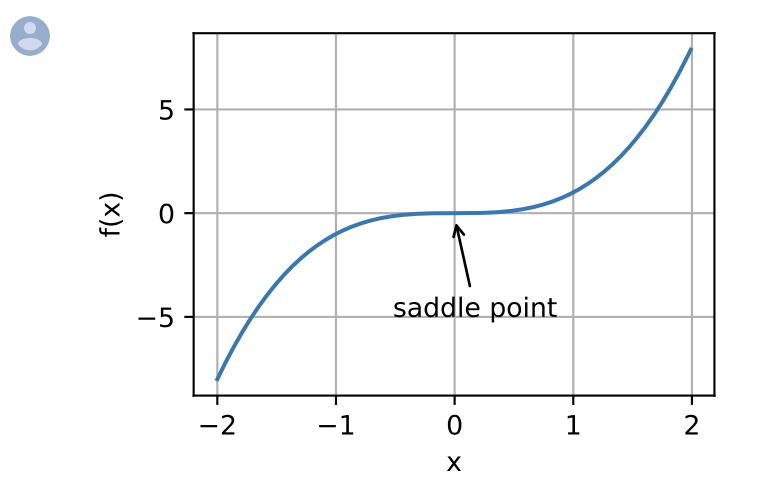 在这里插入图片描述
在这里插入图片描述
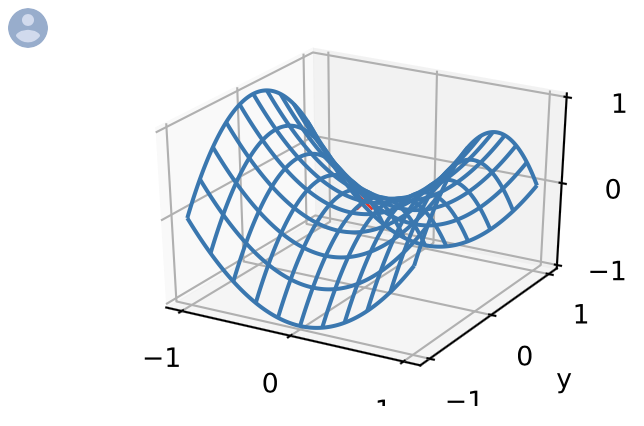
较高维度的鞍点甚至更加阴险。考虑这个函数
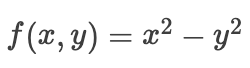 。它的鞍点为
。它的鞍点为 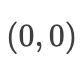 。这是相对于 y的最高值,最低为x 。此外,它 * 看起来像马鞍,这就是这个数学属性的名字的地方。
。这是相对于 y的最高值,最低为x 。此外,它 * 看起来像马鞍,这就是这个数学属性的名字的地方。
2.2 消失渐变
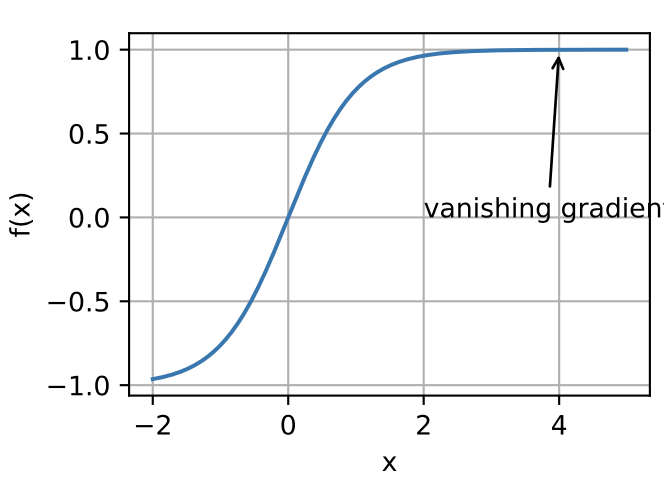
没有必要找到最佳解决方案。本地最佳甚至其近似的解决方案仍然非常有用。

3 凸性
凸性 (convexity)在优化算法的设计中起到至关重要的作用,
这主要是由于在这种情况下对算法进行分析和测试要容易得多。
换言之,如果该算法甚至在凸性条件设定下的效果很差,
通常我们很难在其他条件下看到好的结果。此外,即使深度学习中的优化问题通常是非凸的,
它们也经常在局部极小值附近表现出一些凸性。3.1 convex set
第一组存在不包含在集合内部的线段,所以该集合是非凸的,而另外两组则没有这样的问题。
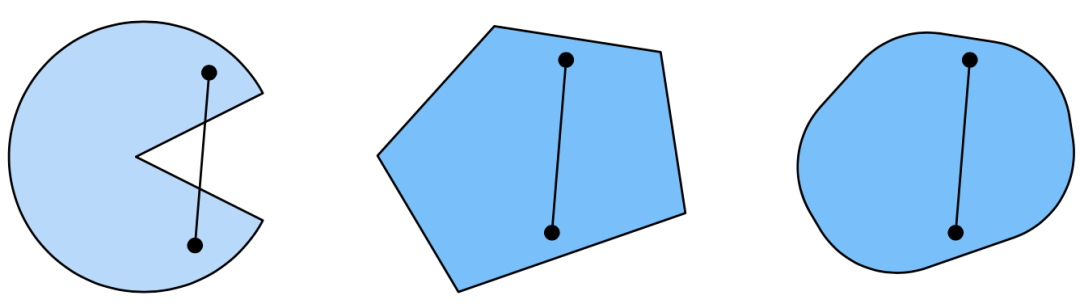 在这里插入图片描述
在这里插入图片描述3.2 凸函数
现在我们有了凸集,我们可以引入凸函数(convex function)。
给定一个凸集 ,如果对于所有 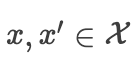 和所有
和所有 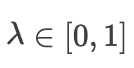 ,一个函数
,一个函数 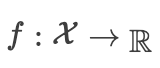 是凸的,我们可以得到为了说明这一点,让我们绘制一些函数并检查哪些函数满足要求。
是凸的,我们可以得到为了说明这一点,让我们绘制一些函数并检查哪些函数满足要求。
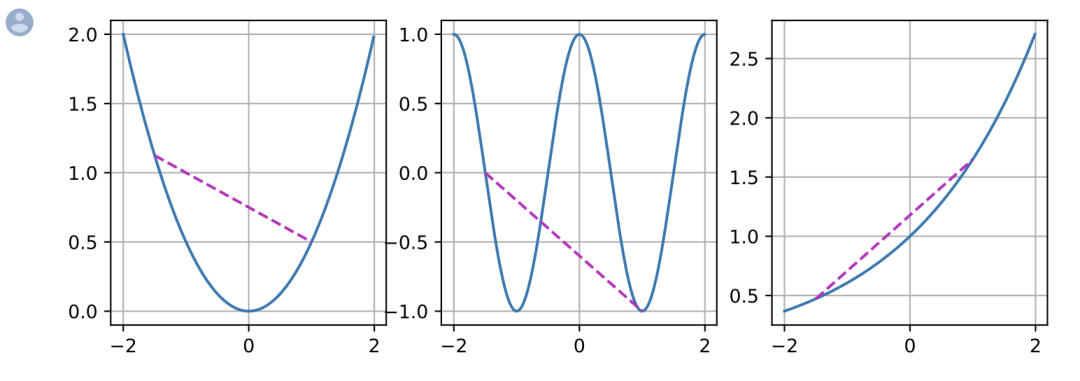
下面我们定义一些函数,包括凸函数和非凸函数。f = lambda x: 0.5 * x**2
# 凸函数
g = lambda x: torch.cos(np.pi * x) # 非凸函数
h = lambda x: torch.exp(0.5 * x) # 凸函数
x, segment = torch.arange(-2, 2, 0.01), torch.tensor([-1.5, 1])
d2l.use_svg_display()
_, axes = d2l.plt.subplots(1, 3, figsize=(9, 3))
for ax, func in zip(axes, [f, g, h]):
d2l.plot([x, segment], [func(x), func(segment)], axes=ax)
4 局部极小值是全局极小值
首先凸函数的局部极小值也是全局极小值。
我们用反证法证明它是错误的:假设 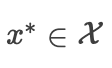 是一个局部最小值,使得有一个很小的正值 ,使得
是一个局部最小值,使得有一个很小的正值 ,使得 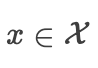 满足
满足 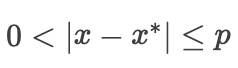 有
有 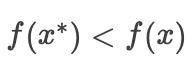 。
。
假设存在 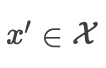 ,其中
,其中 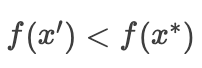 。
。
根据凸性的性质,这与 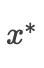 是局部最小值相矛盾。
是局部最小值相矛盾。
因此,对于 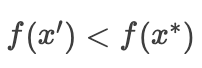 不存在
不存在
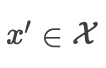 。
。
综上所述,局部最小值 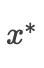 也是全局最小值。例如,对于
也是全局最小值。例如,对于凸函数 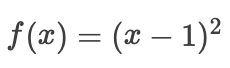 ,有一个
,有一个局部最小值 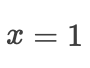 , 它也是
, 它也是全局最小值。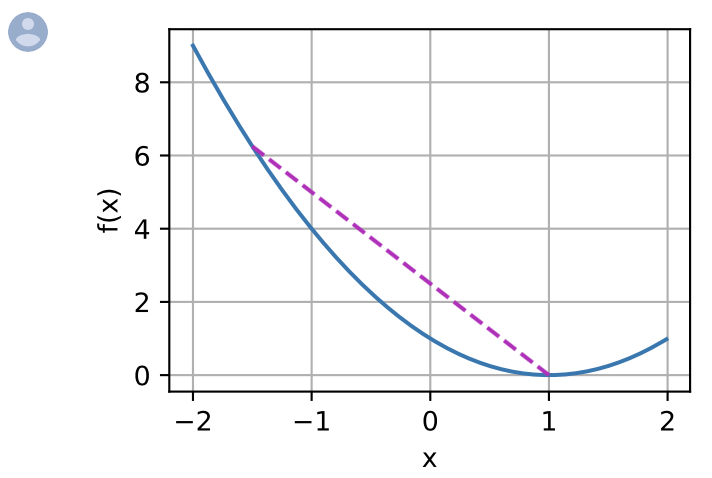 在这里插入图片描述
在这里插入图片描述5 约束
凸优化的一个很好的特性是能够让我们有效地处理约束(constraints)。
即它使我们能够解决以下形式的 约束优化(constrained optimization)问题:这里 是目标函数, 是约束函数。
例如第一个约束 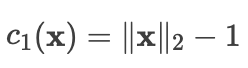 ,则参数 被限制为单位球。
,则参数 被限制为单位球。
如果第二个约束 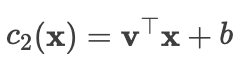 ,那么这对应于半空间上所有的 。
,那么这对应于半空间上所有的 。
同时满足这两个约束等于选择一个球的切片作为约束集。6 总结
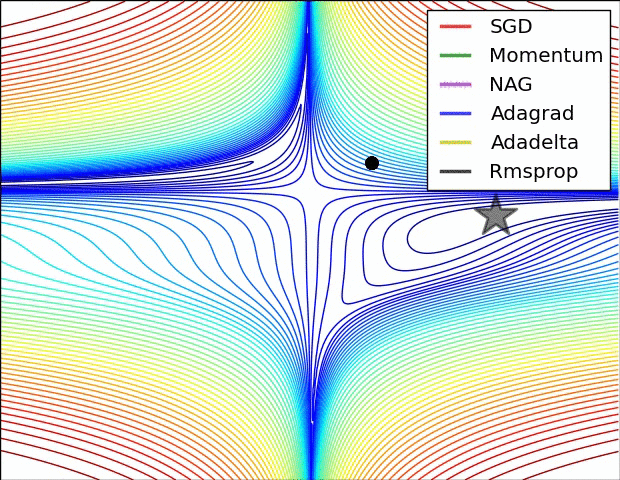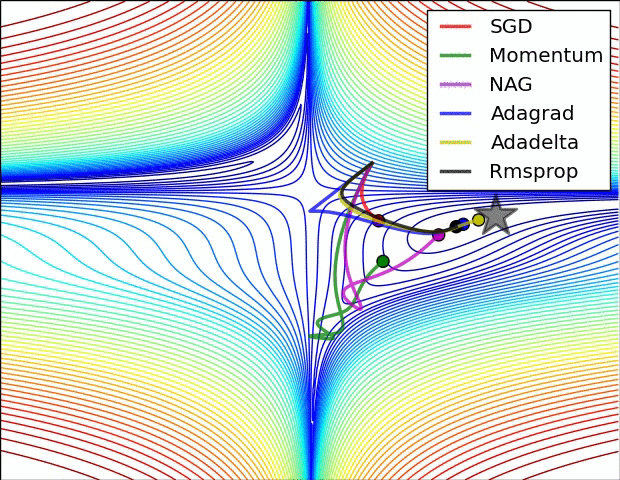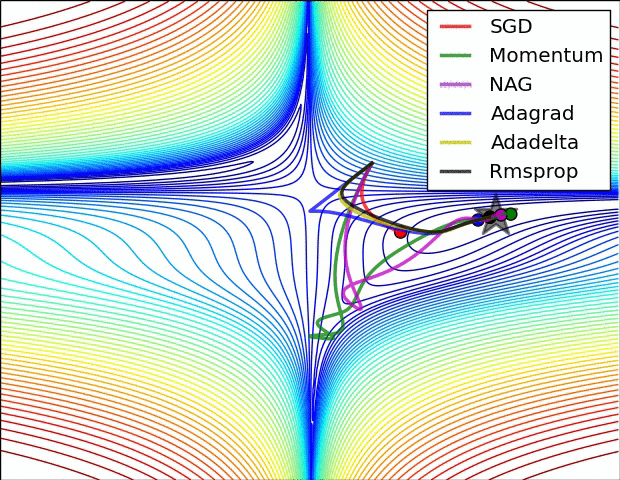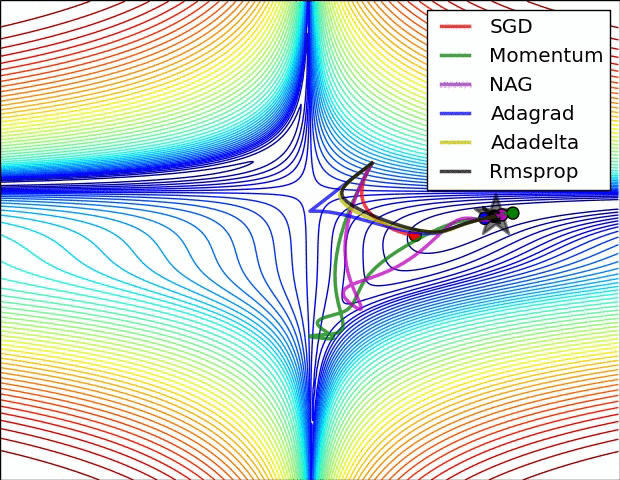 在深度学习的背景下,凸函数的主要目的是帮助我们详细了解优化算法。
在深度学习的背景下,凸函数的主要目的是帮助我们详细了解优化算法。
我们由此得出梯度下降法和随机梯度下降法是如何相应推导出来的。- 根据詹森不等式,“一个多变量凸函数的总期望值”大于或等于“用每个变量的期望值计算这个函数的总值“。
- 一个二次可微函数是凸函数,当且仅当其Hessian(二阶导数矩阵)是半正定的。
- 凸约束可以通过拉格朗日函数来添加。在实践中,只需在目标函数中加上一个惩罚就可以了。
参考
[1].https://zh-v2.d2l.ai/index.html
个人简介:李响Superb,CSDN百万访问量博主,普普通通男大学生,深度学习算法、医学图像处理专攻,偶尔也搞全栈开发,没事就写文章。
博客地址:lixiang.blog.csdn.net



点击下方阅读原文加入社区会员