1. 什么是Holt-Winters
时间序列是非常常见的数据格式,以[时间,观测值]形式表现,如下图。
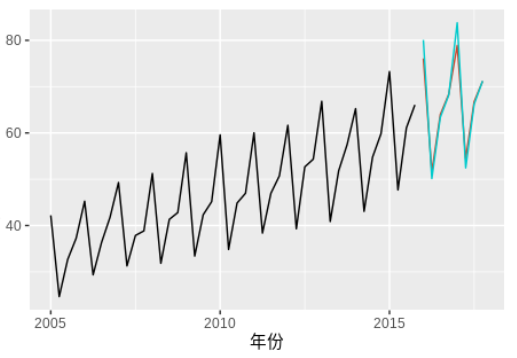
现实场景中如股票走势图,国家GDP历年数据,机器cpu利用率,内存数据等都是时间序列。对未来时间的观测值进行预测是有意义的工作,提前预知未来的数据的走势,可以提前做出行动,如预测cpu使用率,如果cpu飙高,可以及早进行调整,避免机器负载过高而宕机,这个在AIOPS是很常见的一个应用场景。
今天要说到Holt-Winters是利用三次指数平滑来做时间序列预测的方法。Holt-Winters是综合了1957年Holt和1960年Winters两个人的思路的一种方法。
一次指数平滑
我们来看下,一次指数平滑如下图:
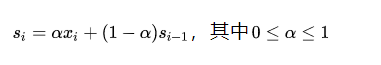
可知,si表示第i时刻的平滑估计,si可以表示为当前实际值xi和上一时刻平滑估计值得加权组合,权重由alpha来决定。那为什么称为指数平滑呢?我们来把式子展开,如下:
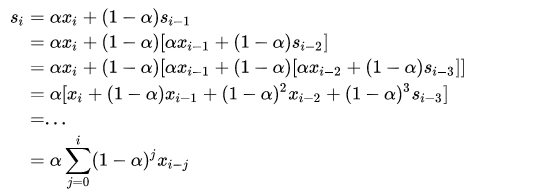
有点类似泰勒展开式的味道
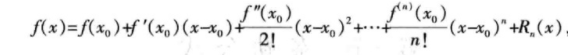
alpha 属于[0, 1], 越大表示近期的数据影响更大
二次指数平滑:加上趋势的因素
一次指数平滑,没有考虑时间序列的趋势和季节性,二次指数平滑加上趋势因素。
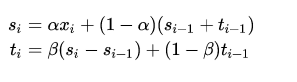
从公式可知,一个时间序列的时刻值分解为baseline部分和趋势部分,t表示趋势,可以表示为连续两个时刻的差值;可知,ti也是一次的指数平滑。
Holt-Winters三次指数平滑:加上季节性因素
在二次指数平滑基础上,考虑季节性因素,就是三次指数平滑,也就是Holt-Winters。由此,一个时间序列的时刻值分解为baseline部分和趋势部分以及季节部分。由于季节性,存在周期,比如按周,按月等。pi季节性为当前季节性值和上一个周期季节性估计值的加权组合,周期在公式中以k来表示。如下:
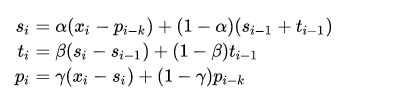
2. Holt-Winters的实现
从第一部分可知,要实现Holt-Winters,只要知道:
•初始值:s0,t0和p0•合适的参数:alpha,beta, gamma•套入公式即可完成预测
三个重要参数:alpha,beta, gamma都属于[0, 1]之间,要么人为的搜索,要么通过数据来估计,通常采用L-BFGS优化算法来拟合数据。优化算法来自包scipy.optimize
的fmin_l_bfgs_b。
from __future__ import divisionfrom sys importexitfrom math import sqrtfrom numpy import arrayfrom scipy.optimize import fmin_l_bfgs_b# 优化算法的loss function,即判断拟合效果,由RMSE MAE等def RMSE(params, *args): Y = args[0] type = args[1] rmse = 0 alpha, beta, gamma = params m = args[2] a = [sum(Y[0:m]) / float(m)] b = [(sum(Y[m:2* m]) - sum(Y[0:m])) / m ** 2]if type == 'additive':
s = [Y[i] - a[0] for i in range(m)] y = [a[0] + b[0] + s[0]]for i in range(len(Y)): a.append(alpha * (Y[i] - s[i]) + (1- alpha) * (a[i] + b[i])) b.append(beta * (a[i + 1] - a[i]) + (1- beta) * b[i]) s.append(gamma * (Y[i] - a[i] - b[i]) + (1- gamma) * s[i]) y.append(a[i + 1] + b[i + 1] + s[i + 1]) rmse = sqrt(sum([(m - n) ** 2for m, n in zip(Y, y[:-1])]) / len(Y))return rmse# 加性的时间序列def additive(x, m, fc, alpha = None, beta = None, gamma = None): Y = x[:]# 利用fmin_l_bfgs_b来估计参数alpha beta和gammaif(alpha == Noneor beta == Noneor gamma == None):
initial_values = array([0.3, 0.1, 0.1]) boundaries = [(0, 1), (0, 1), (0, 1)] type = 'additive' parameters = fmin_l_bfgs_b(RMSE, x0 = initial_values, args = (Y, type, m), bounds = boundaries, approx_grad = True) alpha, beta, gamma = parameters[0]# 初始值 a表示baseline, b表示趋势,s表示季节性,y表示预测值, 分别取第一个周期的统计数据为初始值 a = [sum(Y[0:m]) / float(m)] b = [(sum(Y[m:2* m]) - sum(Y[0:m])) / m ** 2] s = [Y[i] - a[0] for i in range(m)] y = [a[0] + b[0] + s[0]] rmse = 0# 套用上面公式,从0开始,fc表示预测的数量,如已知前7天,预测接下来的一个小时的数据,如果数据粒度是5分钟,fc为12。for i in range(len(Y) + fc):if i == len(Y):
# 预测值为 Y.append(a[-1] + b[-1] + s[-m]) a.append(alpha * (Y[i] - s[i]) + (1- alpha) * (a[i] + b[i])) b.append(beta * (a[i + 1] - a[i]) + (1- beta) * b[i]) s.append(gamma * (Y[i] - a[i] - b[i]) + (1- gamma) * s[i]) y.append(a[i + 1] + b[i + 1] + s[i + 1])# 计算rmse值 rmse = sqrt(sum([(m - n) ** 2for m, n in zip(Y[:-fc], y[:-fc - 1])]) / len(Y[:-fc]))return y[-fc:], alpha, beta, gamma, rmse
另外,statsmodels包中也提供的实现的方法
from statsmodels.tsa.holtwinters importExponentialSmoothing
3. Holt-Winters参数
从上面实现可知,holt-winters通过预估alpha,beta和gamma来预测。算法的关键就是这三个参数和初始化值。三个参数可以通过优化算法来预估,但有可能并不是最优的。初始值的设置除了上面统计值外,还可以通过时序的分解的趋势和季节部分来初始。
import numpy as npfrom pandas import read_csvimport
matplotlib.pyplot as pltfrom statsmodels.tsa.seasonal import seasonal_decomposedecomposition = seasonal_decompose(df_clean.bw, model='additive', period=288)decomposition.plot()
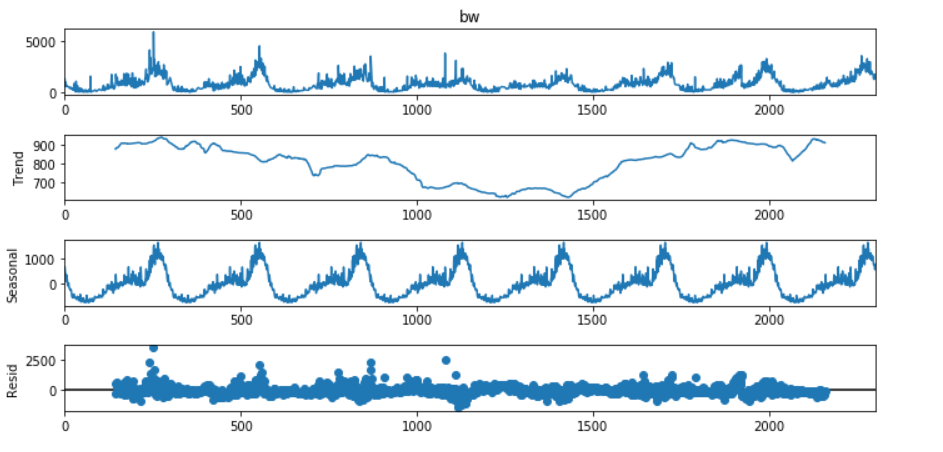
Holt-Winters针对波形比较稳定,没有突刺的情况下,效果会比较好。
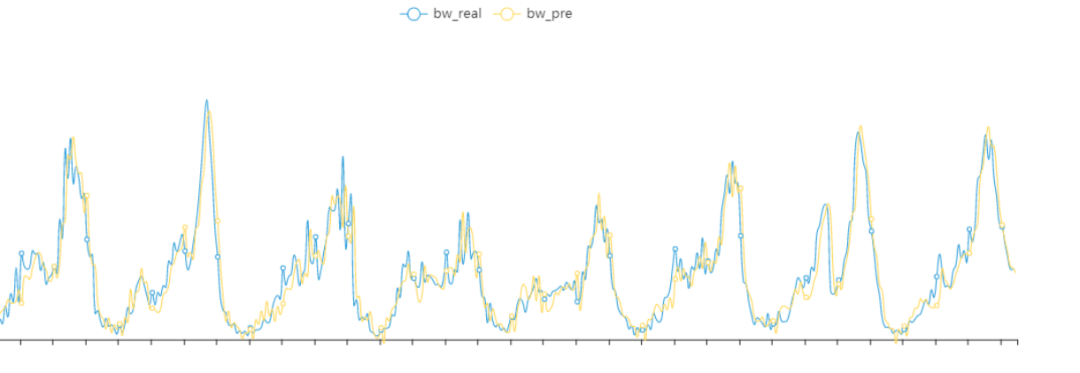
对于存在突刺,统一的alpha,beta,gamma不能很好拟合,预测可能会滞后。
4. 总结
本文分享了时间序列预测算法Holt-Winters以及重要参数的选择,希望对你有帮助。总结如下:
•Holt-Winters是三次指数平滑,分别为baseline,趋势和季节性;•alpha、beta和gamma分别为baseline,趋势和季节性的指数加权参数,一般通过优化算法L-BFGS估计•初始化可通过平均值,也可通过时间序列分解得到•周期m或者k的选择要根据实际数据来选择•Holt-Winters针对波形比较稳定,没有突刺的情况下,效果会比较好
作者简介:wedo实验君, 数据分析师;热爱生活,热爱写作
赞 赏 作 者






点击下方阅读原文加入社区会员