点击下方卡片,关注“慢慢学AIGC”
Arxiv 论文原文:https://arxiv.org/pdf/2209.05433
作者来自:Nvidia,Intel,ARM
以下内容为正文。
摘要
FP8 是推动深度学习训练与推理性能超越现代处理器中常见的 16 位格式(FP16)的自然演进。在本文中,我们提出了一种 8 位浮点(FP8)二进制交换格式,包括两种编码方式:E4M3(4 位指数和 3 位尾数)以及 E5M2(5 位指数和 2 位尾数)。其中,E5M2 遵循 IEEE 754 对特殊值表示的规范,而 E4M3 通过不表示无穷大且仅使用一个尾数字样来表示 NaN(非数字)扩展了其动态范围。
我们在各种图像和语言任务中验证了 FP8 格式的有效性,其效果与 16 位训练所达到的结果质量相当。我们的研究涵盖了当前主流的神经网络架构,包括卷积神经网络(CNN)、循环神经网络(RNN)以及基于 Transformer 的模型,且所有超参数均保持与 16 位基线训练一致。实验还包括规模高达 1750 亿参数的大型语言模型。此外,我们还研究了在 16 位格式训练的语言模型的 FP8 量化后处理,这些模型使用定点 Int8 量化性能较差。
1、引言
深度学习(DL)在当前技术水平上的持续改进需要不断增加神经网络模型的规模以及训练所需的计算资源。例如,大型自然语言模型如 GPT-3 [2]、Turing-Megatron [18]、PaLM [4] 和 OPT [25] 需要在数千个处理器上花费数周时间进行训练。使用低精度数值表示是加速深度学习训练和推理的核心方法。常见的训练浮点类型包括 IEEE 单精度、单精度的 TF32 模式 [19]、IEEE 半精度 FP16 [14] 和 bfloat16 [9]。虽然一些研究尝试将位数压缩到极限(例如 1 位的二进制网络 [5, 7, 26, 24, 17]),但它们未能在许多实际应用中维持所需的结果质量。对于推理,定点的 int8 表示是一种常见选择,但在某些情况下,即使是 int8 推理也可能面临无法满足应用部署所需精度的挑战 [1]。此外,文献中还提出了其他数值表示方法,如对数格式 [15, 11]、posit 表示以及结合 posit 指数值的对数格式 [8],但由于其展示的优势不足以支撑新的算术流水线硬件设计,这些方法尚未在实际中采用。
FP8 是 FP16 的自然演进,它可以降低神经网络训练的计算需求。此外,由于其对实数的非线性采样,FP8 相较于 int8 在推理时可能具有一定优势。Wang 等人 [22] 提出了一种 5 位指数格式用于训练神经网络,并在 CIFAR-10 和 ILSVRC12 数据集的图像分类卷积神经网络(CNN)上验证了他们的方法。Mellempudi 等人 [12] 研究了使用 5 位指数格式对更大规模的 CNN 和基于循环及 Transformer 模块的语言翻译网络进行训练。两篇论文都探讨了使用 16 位权重更新和随机舍入的影响。文献 [20] 首次提出了在训练中使用两种 FP8 格式(4 位和 5 位指数字段),并研究了更多种类的 CNN 以及语音和语言翻译模型。该研究还探讨了使用高精度训练网络的 FP8 推理,并提出利用批量归一化统计值来提高结果准确性。Noune 等人 [16] 提出了一种修改后的 FP8 表示,其中单独为特殊值分配编码以增加表示的动态范围,并深入研究了指数偏置对结果质量的影响。文献 [10] 重点研究了使用多种格式(包括 FP8)的 8 位推理,针对使用更高精度训练的网络进行了实验。
本文中,我们描述了一种用于浮点表示的 8 位二进制格式,其中包括 FP8 的两种编码方式。FP8 在深度学习中的基本应用原则总结于第 2 节。在第 3 节中,我们详细描述了位编码方式及其设计逻辑。第 4 节展示了各种任务和模型的训练与推理的实证评估。我们表明,在不更改任何模型或优化器超参数的情况下,FP8 训练在多种任务及神经网络模型架构和规模上与 FP16 或 bfloat16 训练结果相当。我们的研究包括了规模高达 1750 亿参数的超大语言模型的训练。值得注意的是,需要考虑广泛的模型规模,因为不同规模的模型可能表现出不同的数值行为(例如,在 [12] 中观察到的 ResNet-18 和 ResNet-50 的不同行为)。
2、深度学习中 FP8 的使用要点
FP8 的某些使用特性会影响二进制交换格式的选择。例如,不同网络所需的动态范围决定了需要两种格式,以及更倾向于通过软件而非指数偏置来处理缩放因子。其他方面,例如类型转换的具体细节,与二进制格式无直接关联。这两方面将在本节中简要回顾。
通常情况下,FP8 输入的数学运算会产生更高精度的输出,并在写入内存之前选择性地将结果转换为 FP8。这种做法在当今的 CPU、GPU 和 TPU 上已普遍用于 16 位浮点格式(FP16 和 bfloat16)[3, 14]。例如,矩阵乘法或点积指令会生成单精度输出,而算术强度较低的操作通常会在将 16 位输入转换为单精度后执行。因此,FP8 张量通常通过将宽范围类型(如单精度浮点数)转换为 FP8 生成。
在将高精度值转换为 FP8 之前,需要乘以一个缩放因子以将这些值调整到与对应 FP8 格式可表示范围更好重叠的区间。这类似于混合精度训练中使用 FP16 进行损失缩放(loss scaling)的目的,即将梯度移动到 FP16 可表示的范围内 [14, 13](见幻灯片 13-16)。然而,由于 FP8 的动态范围不足以覆盖所有张量重要值的并集(详见第 3.2 节),某些网络需要每个张量的缩放因子。本论文未深入讨论选择缩放因子的启发式方法,但其总体思路是选择一个缩放因子,使得张量中的最大幅度接近对应格式可表示的最大幅度。对于溢出的值,将其饱和到可表示的最大值。然而,在溢出时跳过权重更新(并降低缩放因子),这一在 FP16 自动混合精度训练 [13] 中使用的策略,并不适合 FP8,因为更窄的动态范围会导致溢出更频繁,从而跳过过多的更新。
在从 FP8 转换回高精度值或在线性运算生成高精度输出后,需要通过乘以缩放因子的倒数来解除缩放。在这两种情况下,只需少量额外算术操作。对于矩阵乘法,解除缩放每个点积只需执行一次,因此成本由许多 FP8 输入的乘加操作摊销。而算术强度较低的操作(如非线性、归一化或优化器的权重更新)通常受限于内存带宽,对每个值增加一个算术指令不敏感。
虽然类型转换的机制与二进制格式无直接关联,但为保证深度学习使用的完整性,我们简要讨论了一些相关方面。从宽精度类型转换为 FP8 时,特殊值会被转换为 FP8 的相应特殊值。对于 E4M3 编码,这意味着宽精度类型(例如单精度)中的无穷大和 NaN 都会在 FP8 中变为 NaN。这种特殊值处理在涉及 FP8 和 FP16 类型的混合精度训练中是必要的,因为自动混合精度 [13] 的运行时损失缩放调整依赖于触发和检测溢出。此外,可以提供非饱和转换模式以满足对溢出有严格要求的用例需求。舍入模式(如舍入到最近偶数、随机舍入等)的选择与交换格式无关,由软件和可能的硬件实现决定,以实现最大灵活性。
3、FP8 二进制交换格式
FP8 包含两种编码方式:E4M3 和 E5M2,其中名称明确表示了指数(E)和尾数(M)位数的数量。我们使用“尾数”这一通用术语,作为 IEEE 754 标准中尾随有效数字字段的同义词(即不包括标准浮点数的隐含前导 1 位的那些位)。FP8 编码的推荐使用方式是:权重和激活张量使用 E4M3,梯度张量使用 E5M2。虽然某些网络可以仅使用 E4M3 或 E5M2 类型进行训练,但有些网络需要两种类型(或者必须大幅减少 FP8 格式的张量数量)。这一点与文献 [20, 16] 的发现一致:推理和训练的前向传播使用 E4M3 的一种变体,而训练中反向传播的梯度使用 E5M2 的一种变体。
FP8 编码的详细信息列在表 1 中。
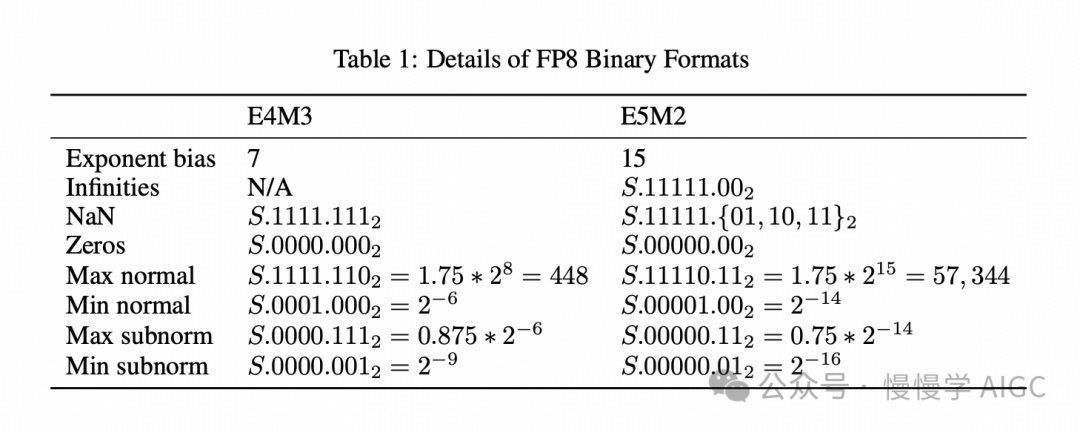
我们在表中使用 S.E.M 的符号表示二进制编码,其中 S 表示符号位,E 表示指数字段(包括偏移指数的 4 位或 5 位),M 表示 3 位或 2 位的尾数。带有下标 2 的数值为二进制表示,否则为十进制表示。
这些 FP8 格式的设计遵循与 IEEE-754 标准一致的原则,仅在预期对深度学习(DL)应用的准确性带来显著收益时才偏离该规范。因此,
E5M2 格式在指数和特殊值的处理上遵循 IEEE 754 规范,可被视为减少了尾数位的 IEEE 半精度(类似于 bfloat16 和 TF32 可被视为减少位数的 IEEE 单精度)。这使得 E5M2 和 IEEE FP16 格式之间的转换非常简单。相比之下,E4M3 的动态范围通过回收大部分用于特殊值的位模式得以扩展,因为对于 E4M3,增加的范围比支持多个特殊值编码对深度学习应用更有用。
3.1 特殊值表示
通过减少特殊值的表示数量,我们扩展了 E4M3 格式较窄的动态范围,将其位模式用于正常值。E4M3 不表示无穷大(有关溢出处理的详细信息,请参见第 2 节),仅保留一种尾数位模式来表示 NaN。这一修改将动态范围额外扩展了一个 2 的幂级别,从 17 个区间(binades)增加到 18 个区间。具体而言,我们增加了七个可表示的幅值(256、288、320、352、384、416、448),它们对应于偏置指数值为 1111₂ 的情况。若无此修改,最大可表示的幅值仅为 240。
为与 IEEE 754 规范保持一致,我们保留了正零和负零以及正 NaN 和负 NaN 的表示形式。虽然通过将零和 NaN 的编码减少到一种可以增加一个额外的可表示幅值(480),但这会破坏 IEEE 754 格式中正负对称性的特性,从而使依赖这一特性的算法实现复杂化或无效化。例如,IEEE 浮点格式允许通过整数操作比较和排序浮点值。将最大值从 448 提高到 480 对深度学习的收益不足以支持偏离 IEEE 规范并放弃依赖该规范的软件实现。
如前所述,E5M2 按照 IEEE 规范一致地表示所有特殊值(无穷大、NaN 和零)。我们的广泛实证研究(见第 4 节)表明,对于深度学习来说,5 位指数为每个张量提供了足够的动态范围(包括次正规值在内的 32 个区间)。此外,与 E4M3 相比,减少特殊值的表示数量对 E5M2 的收益要小得多,因为尾数位更少,E5M2 仅能额外增加 3 个幅值。对于已经提供 32 个区间的 E5M2 来说,再增加一个区间的影响远小于 E4M3 在调整前只有 17 个区间时的影响。
3.2 指数偏置 (Exponent Bias)
E4M3 和 E5M2 都保留了类似 IEEE 的指数偏置,分别为 7 和 15。指数偏置控制了可表示范围在实数轴上的位置。通过为每个张量维护一个比例因子(scale factor)也可以实现相同的效果。我们的实验表明,有些神经网络无法对所有给定类型的张量使用相同的指数偏置,而需要根据每个张量进行调整。在第 4.3 节中讨论了这样的一个例子。因此,我们选择不偏离 IEEE 的指数偏置约定。将每个张量的比例因子留给软件实现比采用可编程的指数偏置方法提供了更大的灵活性——比例因子可以取任意实数值(通常以更高的精度表示),而可编程偏置仅相当于将比例因子限制为 2 的幂次。
4、实验结果
训练实验在模拟的 FP8 环境下进行——张量值被限制为 FP8 能表示的范围(包括比例因子的应用和饱和处理)。例如,在全连接层进行矩阵乘法之前,输入的激活值和权重张量都会被转换为 FP8 格式,然后再转换回更宽的表示(例如 FP16 或 bfloat16)。计算过程使用更宽的表示有两个原因:本论文关注的是交换格式,因为不同处理器可能采用不同的向量或矩阵指令实现,而模拟硬件中不支持的计算会使大模型的训练变得非常缓慢。获得大模型的实验结果是至关重要的,因为以往的研究已经表明,不同规模的模型具有不同的数值行为(例如文献 [12] 中的 R18 和 R50)。
4.1 训练
在 FP8 的训练实验中,我们保留了与高精度基线训练会话相同的模型架构、权重初始化和优化器超参数。基线模型使用 FP16 或 bfloat16 进行训练,已被证明其效果可以与单精度训练相媲美 [14, 9]。在本研究中,我们关注数学密集型操作的输入张量——卷积和矩阵乘法(GEMM 操作,因其涉及点积计算)。因此,除非另有说明,我们将输入到 GEMM 操作的激活值、权重和激活梯度张量剪裁到 FP8 可表示的值范围内。而输出张量则保持更高的精度,因为它们通常被非 GEMM 操作(例如非线性或归一化操作)消耗,并且在许多情况下会与前面的 GEMM 操作融合。将更多张量转移到 FP8 是未来研究的主题。
图像分类任务的结果列于表 2 中。
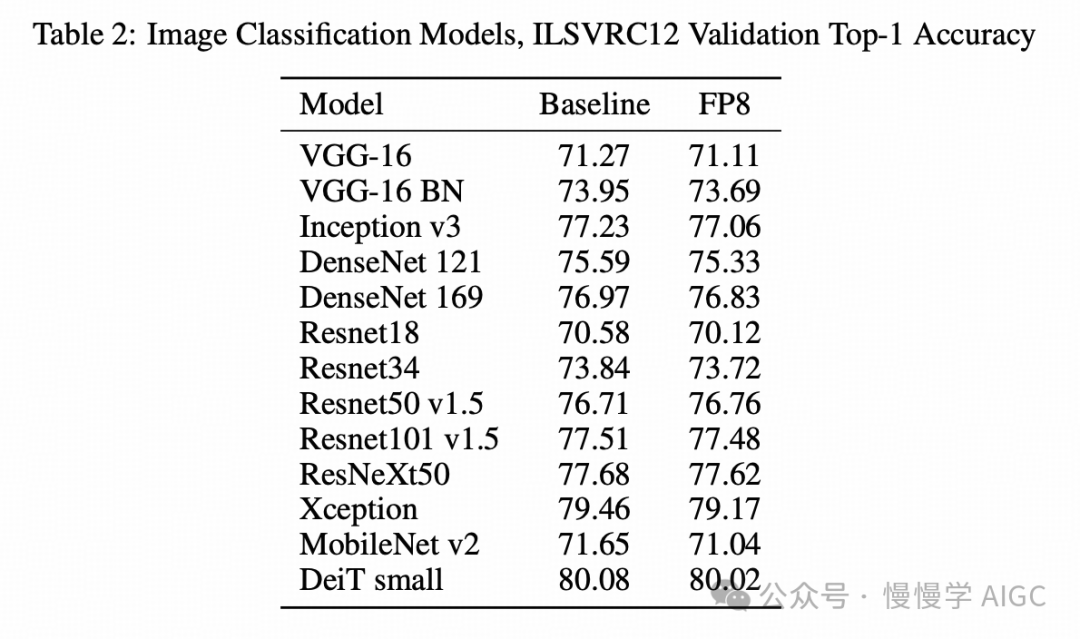
所有网络均在 ImageNet ILSVRC12 数据集上进行训练,使用验证数据集计算 top-1 准确率。所有 GEMM 操作的输入都被剪裁到 FP8,包括第一个卷积层和最后一个全连接层,而这些层在以往的研究 [12, 22] 中通常保持较高的精度。DeiT [21] 是一种基于 Transformer 的架构,其余的模型均为卷积神经网络 (CNN)。除了 MobileNet v2 外,FP8 训练所达到的准确率均在高精度训练的运行间变化范围内(运行间变化指使用不同随机种子初始化训练会话时观察到的准确率差异)。我们正在继续努力恢复 MobileNet v2 的剩余准确率。
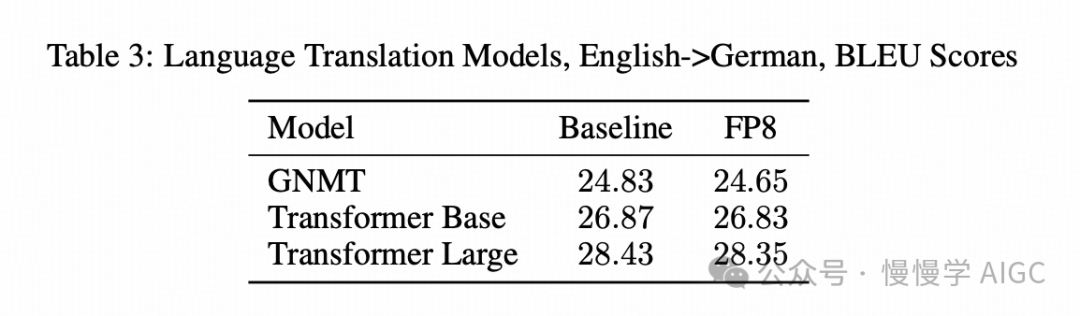
语言翻译任务测试了基于 Transformer 和基于 LSTM 的递归 GNMT 神经网络的表现。尽管基于 Transformer 的翻译模型在实际中已取代了 RNN,但我们仍包含 GNMT,以更全面地涵盖模型架构类型,同时作为仍然使用递归网络的其他任务的参考。模型在 WMT 2016 英语到德语的数据集上进行训练,并使用 sacreBLEU 在 newstest2014 数据上进行评估(BLEU 分数越高越好)。与基线训练会话相比,FP8 训练模型的评估分数在运行间变化范围内。
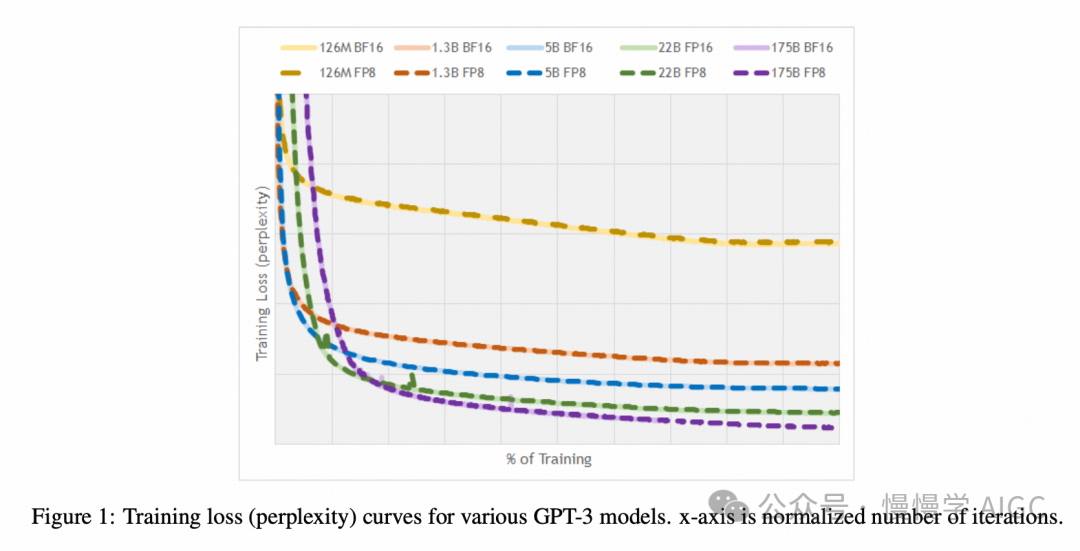
各种语言模型的训练损失(困惑度,值越低越好)列于表 4 中。
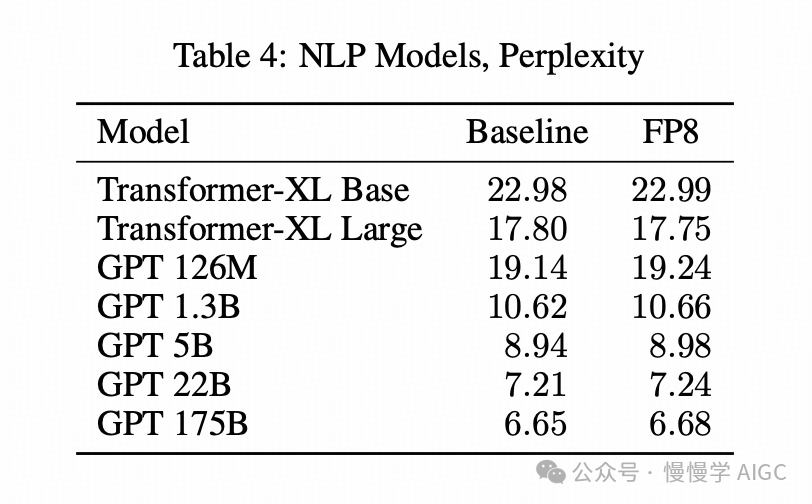
Transformer 模型在 Wikipedia 数据集上进行训练,GPT 模型在 The Pile 数据集的变体上训练,该数据集扩展包含了 Common Crawl 及其衍生数据集,如 [18] 第 3 节所述。与图像网络的观察结果类似,FP8 会话的训练结果在 16 位会话的运行间噪声范围内。需要注意的是,175B 参数模型的困惑度报告于完成 75% 训练时,因为 bfloat16 基线运行尚未完成。而 FP8 训练会话已完成,其损失曲线如图 1 所示,与成功训练一致。与视觉和语言翻译模型类似,我们得出结论,FP8 训练结果与 16 位训练会话的结果一致。
4.2 推理
使用 FP8 训练大大简化了 8 位推理的部署,因为推理和训练使用相同的数据类型。这与使用 32 位或 16 位浮点训练网络的 int8 推理形成了对比,这些网络需要后训练量化 (PTQ) 校准,有时还需要量化感知训练 (QAT) 以维持模型精度。此外,即使使用量化感知训练,一些 int8 量化的模型也可能无法完全恢复浮点模型的精度 [1]。
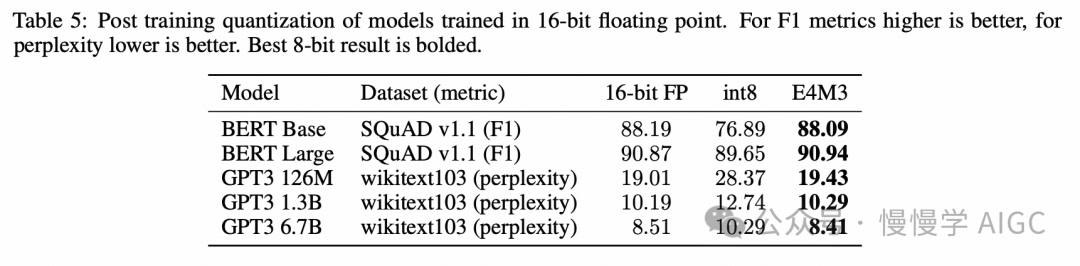
我们评估了将 16 位浮点训练的模型进行 FP8 后训练量化的效果。表 5 列出了 FP16 训练模型在量化为 int8 或 E4M3 后进行推理的准确率。
两种量化方法对权重使用逐通道比例因子,对激活值使用逐张量比例因子,这是 int8 固定点量化的常见做法。所有矩阵乘法操作(包括注意力批量矩阵乘法)的输入张量均被量化。权重采用最大值校准(选择比例因子以表示张量中的最大幅度),激活张量则使用从最大值法、百分位法和最小均方误差法 (MSE) 中选择的最佳校准方法。
在斯坦福问答数据集 (SQuAD) 上对 BERT 语言模型的评估显示,FP8 后训练量化可以保持模型的准确率,而 int8 后训练量化则导致模型精度显著下降。我们还尝试直接将张量转换为 FP8 而不应用比例因子,但这导致了显著的精度下降,困惑度增加到 11.0。在 wikitext103 数据集上对 GPT 模型的评估表明,与 int8 相比,FP8 后训练量化在保留模型精度方面表现更好。
4.3 每张量比例因子
虽然许多网络的训练和推理可以在 FP8 中使用同一种类型张量的相同比例因子成功完成(换句话说,选择单一的指数偏置是可能的),但在某些情况下需要针对每个张量调整比例因子以维持精度。
当我们将更多的张量存储为 FP8 格式时(不仅仅是 GEMM 操作的输入),这种需求更加明显。
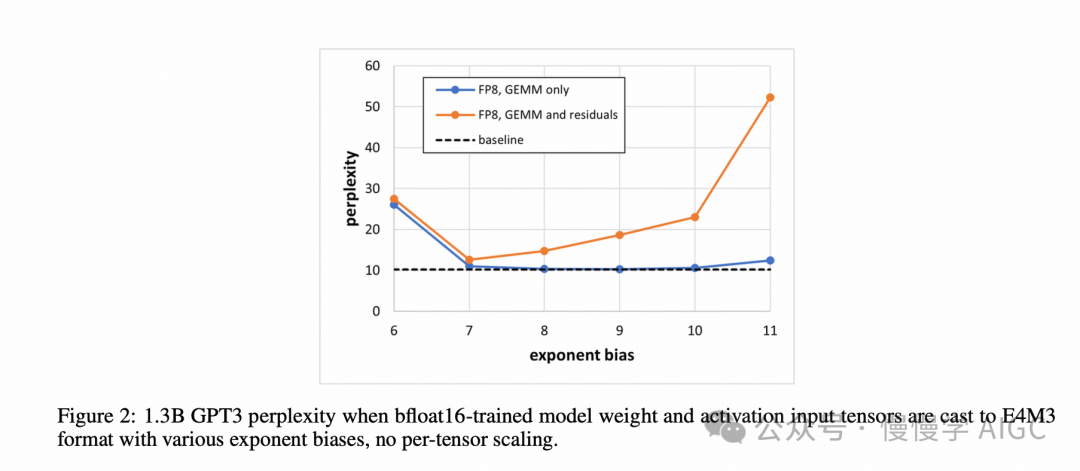
图 2 展示了在 wikitext103 数据集上使用 bfloat16 训练网络进行后训练量化时,FP8 推理的困惑度。未进行校准,权重和激活张量直接从 bfloat16 转换为 E4M3 类型,同时设置了对应的指数偏置。如图所示,当仅将 GEMM 操作的输入(包括加权 GEMM 和涉及激活的两个注意力批量矩阵乘法)转换为 FP8 时,在 [7, 10] 范围内的几个指数偏置选择都能使结果与 bfloat16 基线相匹配。
然而,如果我们还将残差连接(Add 操作的输入张量,也进一步降低了存储和内存带宽压力)量化为 FP8,则没有单一的指数偏置值能够保证足够的精度——即使使用指数偏置 7,困惑度也达到了 12.59,这显著高于 bfloat16 基线的 10.19。然而,如果我们改为校准张量以分配独立的比例因子(遵循 int8 量化的惯例,对权重使用逐通道比例因子,对激活使用逐张量比例因子 [23]),我们在仅量化 GEMM 和量化 GEMM+残差的 FP8 推理中分别实现了 10.29 和 10.44 的困惑度。
5、结论
本文提出了一种 FP8 二进制交换格式,包括 E4M3 和 E5M2 编码。通过尽量遵循 IEEE-754 对浮点数二进制编码的约定,我们确保软件实现可以继续依赖 IEEE 浮点数的性质,例如使用整数操作比较和排序值的能力。
该格式的主要动机是加速深度学习的训练和推理,通过启用更小且更高效的数学流水线并减少内存带宽压力。我们证明了,在图像和语言任务中,使用 FP8 训练的各种神经网络模型可以与 16 位训练会话达到相同的模型精度,同时保持相同的模型、优化器和训练超参数。
使用 FP8 不仅加速了训练并减少了资源需求,还通过训练和推理使用相同的数据类型简化了 8 位推理的部署。在 FP8 出现之前,8 位推理需要对使用浮点训练的 int8 模型进行校准或微调,这增加了部署过程的复杂性,并且在某些情况下无法保持精度。
扫描下方二维码,关注“慢慢学AIGC”
